算法——链表
链表常用技巧
- 画图分析！！！！！！！！！！——直观形象，便于理解、大多数都是模拟
- 引入虚拟头结点（哨兵位）
- 典型的就是在第一个节点传空指针，此时我们如果解引用，程序直接崩掉
-
我们一般选择创建哨兵位头结点，这里我们哨兵位不存储数据。解释传入空链表，这里的newhead只需要特判一下即可
-
不要吝啬空间，大胆定义变量。
- 我们经常会遇到这种题目，将cur插入到prev后面。途中四句是正确的顺序，在考试题目中经常会遇到将这四句顺序打乱的情况。其实我们只需要保证前两句先执行即可（五角星标志的），这样是为了防止prev找不到next。如果先执行后两句，那么prev链接cur之后，就找不到next节点
2. 我们也可以定义next指针，这样就不需要考虑下面四句语句的执行顺序
- 链表快慢双指针，典型题目有：判环；找链表中环的入口；找链表中倒数第n个节点
链表中常用操作
- 创建一个新节点 new
- 尾插：先定义一个指针tail指向最后一个位置，让tail->next 指向新节点,然后将尾结点转移到新节点上。
- 头插：让新节点的next指向newhead->next，此时如果之前给的链表为空，让新节点next指向空，不会发生访问空节点的报错。然后让newhead->next指向新节点。如果怕链表断开，可以新定义一个next指针。我们也可以利用这个方法完成逆序链表
两数相加
两数相加
题目解析
这里给我们逆序存储链表反而有利于我们做题，我们相加时是从最低位开始加，如果题里给我们正常顺序存储的链表的话，我们还需要自己逆置。
算法原理
解法：模拟两数相加的过程
- 这里创建一个newhead用于链接最终结果。如果这里我们不用newhead链接，我们需要先把两个链表头结点相加然后存储新的head用来记录结果（因为最后要返回链表），然后再继续往后相加。这样我们操作就多了一步。
- 用一个变量t来标记我们的进位，然后定义两个指针模拟加法。只要cur1、cur2不为空，就把他们指向的数字移到t中，然后把t中个位数字提出来（因为数字相加可能变为两位数，牵扯到进位），然后把new一个节点7，链接到到我们的newhead后面。同理…
代码实现
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2)
{
ListNode* cur1 = l1, *cur2 = l2;
ListNode* newhead = new ListNode(0); // 创建⼀个虚拟头结点，记录最终结果
ListNode* prev = newhead; // 尾指针
int t = 0; // 记录进位
while(cur1 || cur2 || t)
{
// 先加上第⼀个链表
if(cur1)
{
t += cur1->val;
cur1 = cur1->next;
}
// 加上第⼆个链表
if(cur2)
{
t += cur2->val;
cur2 = cur2->next;
}
prev->next = new ListNode(t % 10);
prev = prev->next;
t /= 10;
}
prev = newhead->next;
delete newhead;
return prev;
}
};
两两交换链表中的节点
两两交换链表中的节点
题目解析
- 给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。
算法原理
解法：循环迭代：
- 这里同样引入一个虚拟节点newhead链接链表。如果不引入头结点，在我们交换前两个节点的时候，因为前面没有节点。所以我们要先定义一个变量找到最终要返回的头结点。因为前半部分1、2两个节点是不需要将修改将前面的指针指向2，但是后面部分3、4需要交换过后，让前面位置的指针指向4链接。这时需要写两段代码分别写两种情况。
- 不要吝啬我们的空间，定义四个指针，紫色情况是交换1、2，绿色情况是交换3、4
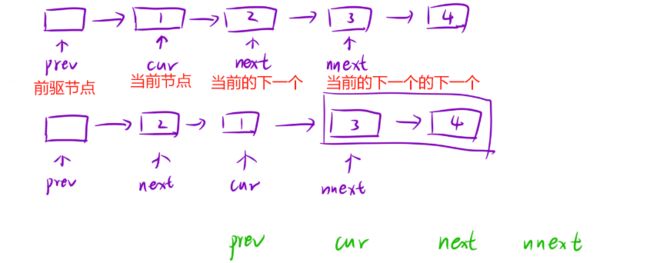
- 当3、4交换完成时，四个指针移动如下情况：
- 当链表是奇数个节点，这时cur有可能访问空指针，所以我们需要终止循环
- 当链表是偶数个节点时，next指向空，需要终止循环。
- 当链表是奇数个节点，这时cur有可能访问空指针，所以我们需要终止循环
所以终止循环条件：cur或者next有一个指向空的时候，就终止循环
代码实现
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
if(head == nullptr || head->next == nullptr) return head;
ListNode* newHead = new ListNode(0);
newHead->next = head;
ListNode* prev = newHead, *cur = prev->next, *next = cur->next, *nnext =next->next;
while(cur && next)
{
// 交换结点
prev->next = next;
next->next = cur;
cur->next = nnext;
// 修改指针
prev = cur; // 注意顺序
cur = nnext;
if(cur) next = cur->next;
if(next) nnext = next->next;
}
cur = newHead->next;
delete newHead;
return cur;
}
};
重排链表
重排链表
题目解析
- 第一个、倒数第一个、第二个、倒数第二个
算法原理
**解法：模拟——**其实很像两个链表合并，一个是正向的1、2，一个是倒向的链表4、3。恰好是原始链表的前半部分，和后半部分逆序。
所以我们的策略是：先找到链表的中点，然后把后面部分的链表逆序；然后把前面的部分和后面的部分一个一个交互链接，合并一起即可。
-
找到链表的中间节点（⼀定要画图考虑 slow 的落点在哪⾥ ）
- 利用快慢双指针。这里注意一下节点个数是奇数和偶数的情况。slow=slow->next;fast=fast->next->next;我们的停止循环的条件是当fast或fast->next为空。如下图分别是节点个数为奇数和偶数的情况。此时观察slow落在中点的情况：
- 我们可以让slow->next部分直接翻转。这里我们可能会有疑惑，难道不应该让slow后面的部分整体翻转吗？这是这道题的特殊性，我们还是用1234进行举例子，我们发现重排前和重拍后发现2和3的链接部分是不变的，所以我们可以把slow指向的这个节点大胆给第一个链表。重排后发现是不影响结果的。
- 利用快慢双指针。这里注意一下节点个数是奇数和偶数的情况。slow=slow->next;fast=fast->next->next;我们的停止循环的条件是当fast或fast->next为空。如下图分别是节点个数为奇数和偶数的情况。此时观察slow落在中点的情况：
2. 我们也可以让slow所指的开始翻转（红色笔标注的）。此时无非是把slow所指的节点丢给后半部分，逆序合并后发现结果并不影响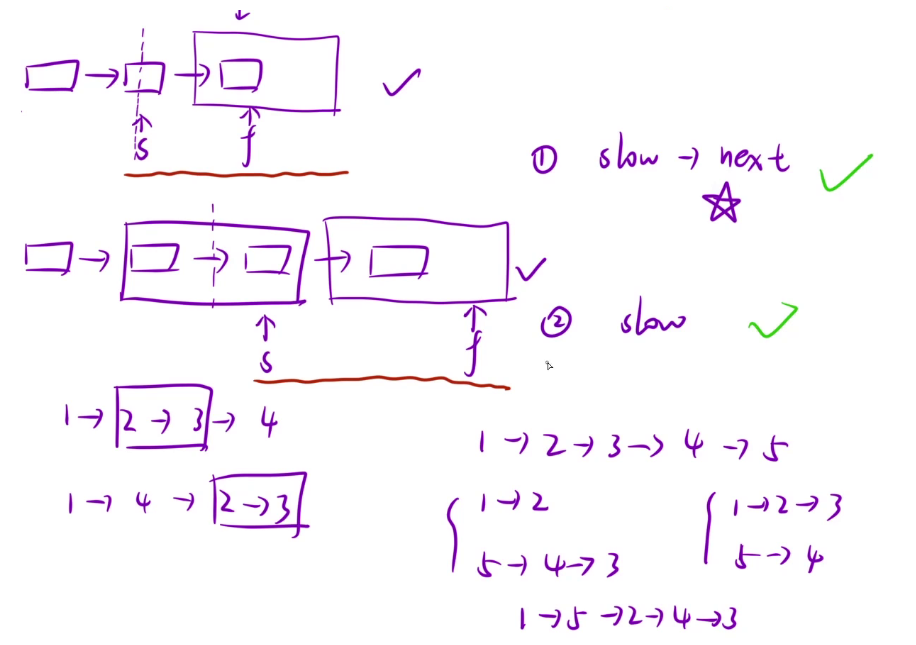
- 用头插法，如果这里使用头插法，建议使用第一个方法（slow->next翻转）。因为最终是断开成两个链表，
- 如果从slow所指的位置开始逆置，会发现箭头所指的位置指针无法断开。有可能出现意想不到的错误；
2. 当我们选择slow->next位置开始翻转，我们只需让slow所指的位置置空即可，
3. 如果我们只能用slow位置开始翻转的情况时，我们可以引入一个虚拟头结点newhead（哨兵位），去链接head，然后在快慢指针找中间节点，之前是slow位置，就会变成slow->next，这时候也能将两个链表断开。
- 把slow后面部分逆序——头插法（使用虚拟头结点）
- 把slow后面的节点，头插到新建的头（哨兵位）结点后面。当让cur头插到newhead后面时，先让cur->next指向空（就是newhead2后面的节点），然后newhead2->next指向cur，此时newhead2就与null（原先后面的节点）断开
- 当newhead2后面有节点时，按照上面的操作我们会发现，newhead2会与后面的断开了，所以在刚开始头插时我们要定义一个next指针标记newhead2后面的节点。当执行完上面操作后，让cur=next
- 合并两个链表
- 我们是创建一个虚拟节点，让他们都尾插在这后面
- cur1相较于cur2会长一些，所以循环判空条件为cur1为空。
代码实现
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
void reorderList(ListNode* head)
{
// 处理边界情况
if(head == nullptr || head->next == nullptr || head->next->next == nullptr)
{
return ;
}
// 1. 找到链表的中间节点 - 快慢双指针（⼀定要画图考虑 slow 的落点在哪⾥）
ListNode* slow = head, *fast = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
// 2. 把 slow 后⾯的部分给逆序 - 头插法
ListNode* head2 = new ListNode(0);
ListNode* cur = slow->next;
slow->next = nullptr; // 注意把两个链表给断开
while(cur)
{
ListNode* next = cur->next;
cur->next = head2->next;
head2->next = cur;
cur = next;
}
// 3. 合并两个链表 - 双指针
ListNode* ret = new ListNode(0);
ListNode* prev = ret;
ListNode* cur1 = head, *cur2 = head2->next;
while(cur1)
{
// 先放第⼀个链表
prev->next = cur1;
cur1 = cur1->next;
prev = prev->next;
// 再放第⼆个链表
if(cur2)
{
prev->next = cur2;
prev = prev->next;
cur2 = cur2->next;
}
}
delete head2;
delete ret;
}
};
合并k个升序链表
合并k个升序链表
题目解析
算法原理
**解法一：暴力解法：**逐个合并.其中n是链表的长度，k为链表的个数
解法二：优先级队列做优化
我们可以直接定义k个指针，仿照合并k个有序链表，把这些链表中较小的头结点放到newhead后面，放完之后右移，继续比较各个节点最小的，把最小的连接在newhead后面即可。这样只需要遍历一遍链表即可。O(n*k)是理想状态下的时间复杂度，我们还要找出k个节点中最小的节点。这里我们可以利用优先级队列
把k个节点丢入小根堆里，经过排序后，堆顶元素即为最小的元素，链接到newhead后面后，将移动后下一个节点放入小根堆里。这里时间复杂度O(nklogk)
解法三：分治——递归
流程：
- 特判，如果题⽬给出空链表，⽆需合并，直接返回；
- 返回递归结果。
递归函数设计：
- 递归出⼝：如果当前要合并的链表编号范围左右值相等，⽆需合并，直接返回当前链表；
- 应⽤⼆分思想，等额划分左右两段需要合并的链表，使这两段合并后的⻓度尽可能相等；
- 对左右两段分别递归，合并[l,r]范围内的链表
- 再调⽤mergeTwoLists函数进⾏合并（就是合并两个有序链表）
时间复杂度：一共k个链表，每个链表里面有n个节点，每一层我们都平均分，即高度为logk，每一个节点都执行了logk次合并（这棵树的高度次）
代码实现
class Solution
{
struct cmp
{
bool operator()(const ListNode* l1, const ListNode* l2)
{
return l1->val > l2->val;
}
};
public:
ListNode* mergeKLists(vector<ListNode*>& lists)
{
// 创建⼀个⼩根堆
priority_queue<ListNode*, vector<ListNode*>, cmp> heap;
// 让所有的头结点进⼊⼩根堆
for(auto l : lists)
if(l) heap.push(l);
// 合并 k 个有序链表
ListNode* ret = new ListNode(0);
ListNode* prev = ret;
while(!heap.empty())
{
ListNode* t = heap.top();
heap.pop();
prev->next = t;
prev = t;
if(t->next) heap.push(t->next);
}
prev = ret->next;
delete ret;
return prev;
}
};
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution
{
public:
ListNode* mergeKLists(vector<ListNode*>& lists)
{
return merge(lists, 0, lists.size() - 1);
}
ListNode* merge(vector<ListNode*>& lists, int left, int right)
{
if(left > right) return nullptr;
if(left == right) return lists[left];
// 1. 平分数组
int mid = left + right >> 1;
// [left, mid] [mid + 1, right]
// 2. 递归处理左右区间
ListNode* l1 = merge(lists, left, mid);
ListNode* l2 = merge(lists, mid + 1, right);
// 3. 合并两个有序链表
return mergeTowList(l1, l2);
}
ListNode* mergeTowList(ListNode* l1, ListNode* l2)
{
if(l1 == nullptr) return l2;
if(l2 == nullptr) return l1;
// 合并两个有序链表
ListNode head;
ListNode* cur1 = l1, *cur2 = l2, *prev = &head;
head.next = nullptr;
while(cur1 && cur2)
{
if(cur1->val <= cur2->val)
{
prev = prev->next = cur1;
cur1 = cur1->next;
}
else
{
prev = prev->next = cur2;
cur2 = cur2->next;
}
}
if(cur1) prev->next = cur1;
if(cur2) prev->next = cur2;
return head.next;
}
};
k个一组翻转链表
k个一组翻转链表
题目解析
链表中的节点每k个一组进行翻转，如果剩余的链表不够k个，则不翻转
算法原理
解法：模拟
- 先求出需要逆序多少组n：遍历链表一遍 n=链表节点个数/k
- 重复n次长度为k的链表的逆序
- 利用头插法逆序，创建一个newhead。头插时，cur->next=head->next;head->next = cur;此时右边节点（2）会丢失，需要先用一个next指针记录一下节点，然后头插。头插完之后cur++，直至头插3之后，这一组完成。
- 进行下一组头插时，需要将4头插到1的后面，所以需要一个指针标记一下1的位置，这个位置是每一组开始头插的第一个位置。所以每组第一个位置开始头插的时候，要标记好开始头插的位置（tmp），还需要定义个prev标记将要头插位置的前驱，每当一组头插完，该进行下一组时，让prev更新到tmp位置。
代码实现
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
// 1. 先求出需要逆序多少组
int n = 0;
ListNode* cur = head;
while(cur)
{
cur = cur->next;
n++;
}
n /= k;
// 2. 重复 n 次：⻓度为 k 的链表的逆序即可
ListNode* newHead = new ListNode(0);
ListNode* prev = newHead;
cur = head;
for(int i = 0; i < n; i++)
{
ListNode* tmp = cur;
for(int j = 0; j < k; j++)
{
ListNode* next = cur->next;
cur->next = prev->next;
prev->next = cur;
cur = next;
}
prev = tmp;
}
// 把不需要翻转的接上
prev->next = cur;
cur = newHead->next;
delete newHead;
return cur;
}
};