【C/C++ 数据结构】-二叉树(1)
作者:学Java的冬瓜
博客主页:☀冬瓜的主页
专栏:【C/C++ 数据结构和算法】
文章目录
- 一、树
-
- 1、树的概念
-
- 1.1、树的特点
- 1.2、树的相关概念
- 2、树的表示
- 3、树的应用
- 二、二叉树
-
- 1、二叉树的概念
- 2、特殊的二叉树
-
- 2.1、满二叉树
-
- @概念
- @总结点数及满二叉树高度
- 2.2、完全二叉树
-
- @概念
- @总结点分析
- 3、二叉树的性质
-
- 3.1、相关性质
- 3.2、二叉树性质选择题练习
- 4、二叉树的存储结构
-
- 4.1、顺序存储
- 4.2、链式结构
- 5、二叉树的遍历
-
- 5.1、前中后序遍历
-
- @代码
- @前序画图分析
- @快速建立一个二叉树方法
- 5.2、层序遍历
-
- @代码
-
- 1>、队列的实现
- 2>、实现层序遍历
- 3>、核心代码
- @画图分析
- 6、求二叉树总结点数
- 7、求叶子节点的个数
- 8、求二叉树的深度
- 9、销毁二叉树
- 三、总结
- 四、习题补充
-
- 1、二叉树是否存在value值
- 2、查找第k层节点个数
- 3、翻转二叉树
- 4、检查两棵树是否相同
- 5、层序遍历(Push和Pop有返回值版)
一、树
1、树的概念
概念:树是一种非线性的数据结构,它是有n(n>=0)个有限节点组成一个具有层次关系的集合。
树:把它叫做树是因为它看起来像一棵倒挂的树,即根朝上,叶朝下
1.1、树的特点
- 子树是不相交的
- 除了根节点(没有父节点)外,每个节点有且只有一个父节点。
- 一棵N个节点的树有N-1条边
1.2、树的相关概念
1.2.1、节点和度:
- 节点的度:一个节点含有的子树的个数称为该节点的度。
- 树的度:一棵树中,最大的节点的度,称为。
- 叶节点/终端节点:度为0的节点。
- 双亲节点/父节点:有子节点的节点。
- 子节点:一个节点含有的子树的根节点,称为该节点的子节点。
- 兄弟节点:具有相同父节点的节点。
1.2.2、树的深度和森林
- 节点的层次:从跟开始定义起,跟为第1层,跟的子节点为第二层,以此类推。
- 树的高度/深度:树中节点的最大层次。
- 森林:由m(m>0)棵互不相交的多棵树集合称为森林。(数据结构中的并查集本质上就是一个森林)。
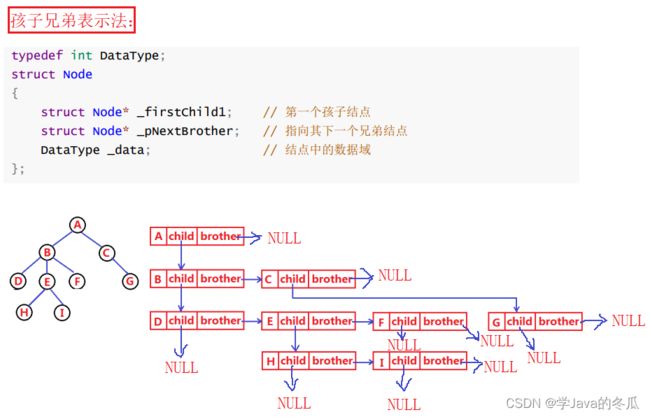
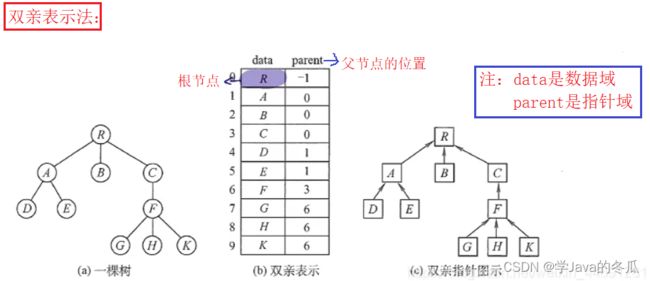
2、树的表示
说明:有多种表示树的方式:双亲表示法、孩子表示法、孩子兄弟表示法
方法优劣:
1、其中孩子兄弟表示法相对来说更常用。
2、双亲表示法对父节点操作为O(1),但对子节点操作要遍历整棵树。
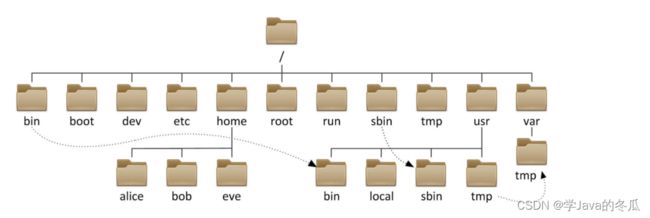
3、树的应用
说明:表示文件系统的目录树结构。
二、二叉树
1、二叉树的概念
概念:
一棵二叉树是节点的一个有限集合,该集合或者为空,或者为由一个根节点加上一棵左子树和一棵右子树组成。
特点:
1、每个节点最多有两棵子树,即二叉树不存在度大于2的节点
2、二叉树的子树有左右之分,其子树的次序不能颠倒。
2、特殊的二叉树
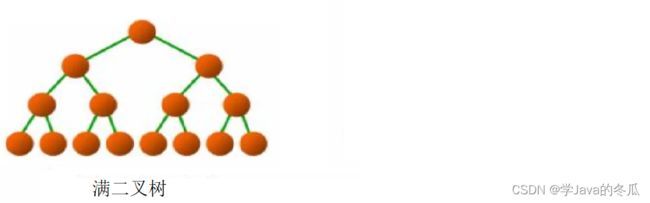
2.1、满二叉树
@概念
概念:一个二叉树,如果每一层的节点数都达到最大值,那这个二叉树就是满二叉树。
性质:设h为二叉树的层数(深度),节点数为2^h-1个。
@总结点数及满二叉树高度
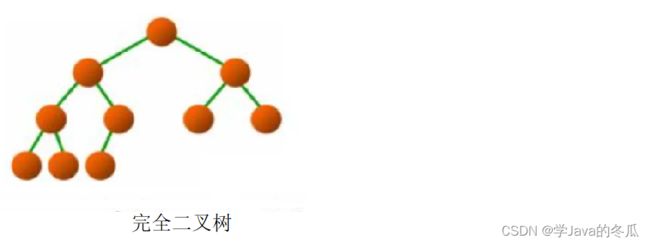
2.2、完全二叉树
@概念
说明:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树引出来的。
概念:
设二叉树深度为h,1、除了第h层外,其它层(1~h-1)层的节点均为满节点,2、第h层的节点都连续集中在最左边。
@总结点分析
3、二叉树的性质
3.1、相关性质
- 第i层节点:若规定根节点的层数为1,则一棵非空二叉树在第i层上最多有2^(i-1)个节点
- 最大节点数:若规定根节点层数为1,则深度为h的树,最大节点数为2^h-1。
- 度为0节点数和度为2节点数关系:对于任意一棵二叉树,它的度为0的叶节点的个数n0,和度为2的节点个数n2关系:n0=n2+1。
- 满二叉树深度:若规定根节点的层数为1,有n个节点的满二叉树的深度约为:h=logn
3.2、二叉树性质选择题练习
4、二叉树的存储结构
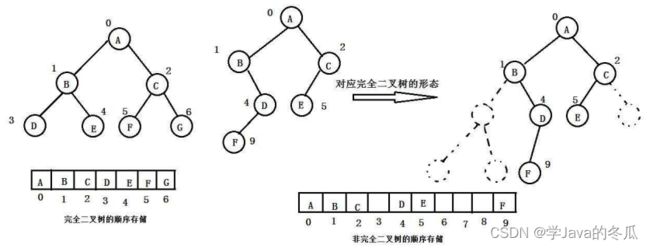
4.1、顺序存储
说明:顺序结构存储就是用数组来存储,一般使用数组只适合表示完全二叉树,如果不是表示完全二叉树,会有空间的浪费。而现实中使用,只有堆(后续内容)才会使用数组。
二叉树顺序存储在物理上是一个数组,在逻辑上是一棵二叉树。
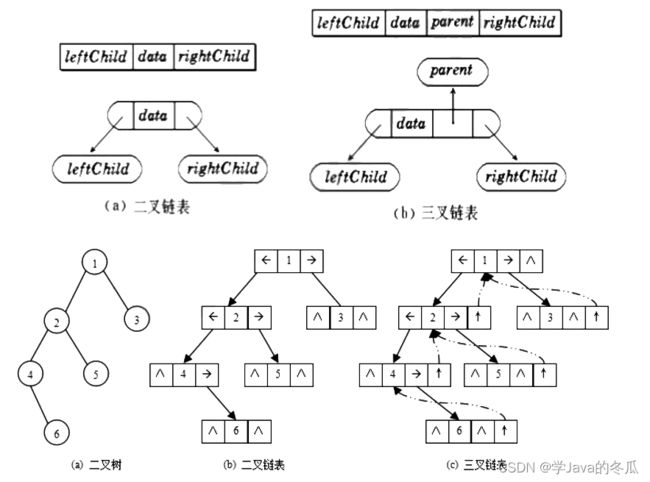
4.2、链式结构
说明:用链表来表示二叉树。一般链表中每个节点由三个域组成,数据域,左右指针域。左右指针分别指向左右子树的根节点。
等后面学到高阶数据结构红黑树会出现三叉链表(即还有一个指针指向当前节点的父节点)
5、二叉树的遍历
5.1、前中后序遍历
@代码
//结构体声明
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
//前序
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%c ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
//中序
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}
//后序
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}
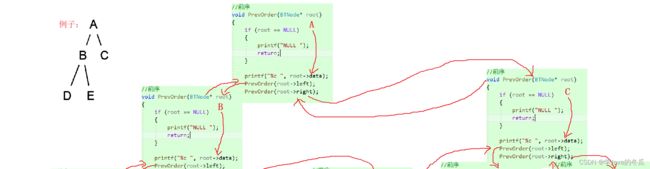
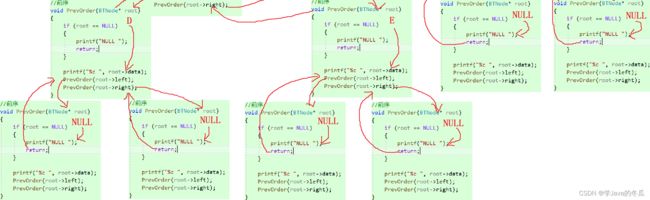
@前序画图分析
前序:1>先判断是否为空,2>不为空就先打印该节点数据,3>再递归左子树,递归右子树。4>若第1步判断为NULL,则直接return。中序和后序的原理相同。
中序后序:其中中序是执行完左子树才开始打印该节点数据,而后序则是左子树右子树都执行完,才打印该节点数据。
@快速建立一个二叉树方法
方法:一个节点一个节点得申请空间并初始化,最后连起来。
int main()
{
BTNode* A = (BTNode*)malloc(sizeof(BTNode));
A->data = 'A';
A->left = NULL;
A->right = NULL;
BTNode* B = (BTNode*)malloc(sizeof(BTNode));
B->data = 'B';
B->left = NULL;
B->right = NULL;
BTNode* C = (BTNode*)malloc(sizeof(BTNode));
C->data = 'C';
C->left = NULL;
C->right = NULL;
BTNode* D = (BTNode*)malloc(sizeof(BTNode));
D->data = 'D';
D->left = NULL;
D->right = NULL;
BTNode* E = (BTNode*)malloc(sizeof(BTNode));
E->data = 'E';
E->left = NULL;
E->right = NULL;
A->left = B;
A->right = C;
B->left = D;
B->right = E;
PostOrder(A);
return 0;
}
5.2、层序遍历
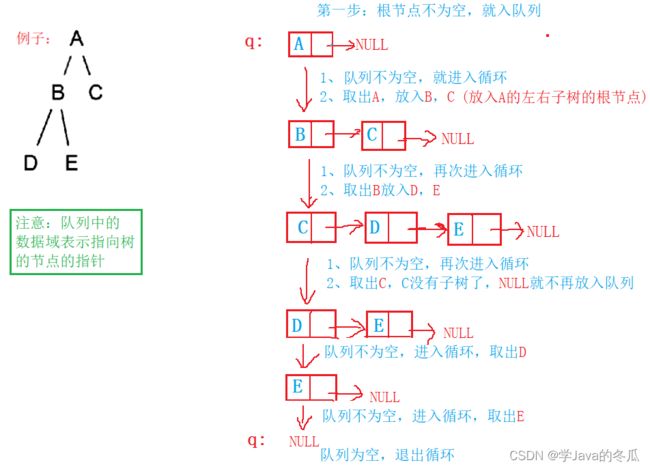
说明:从层数为1的根节点出发,从上到下,从左到右一层一层的访问树中节点的过程就是层序遍历。借用队列来实现,利用了队列先入先出的思想。
核心思路:上一层节点出的时候带下一层节点进。
@代码
1>、队列的实现
#pragma once
#include 2>、实现层序遍历
#define _CRT_SECURE_NO_WARNINGS
#include "Queue.h"
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
//层序遍历
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
//1、先把树的根节点入队列
if (root != NULL)
{
QueuePush(&q, root);
}
//2、队列不为空,二叉树的该节点出队列,该节点的两个子树的根节点入队列
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%c ", front->data);
QueuePop(&q);
if (front->left != NULL)
{
QueuePush(&q, front->left);
}
if (front->right != NULL)
{
QueuePush(&q, front->right);
}
}
QueueDestroy(&q);
}
int main()
{
BTNode* A = (BTNode*)malloc(sizeof(BTNode));
A->data = 'A';
A->left = NULL;
A->right = NULL;
BTNode* B = (BTNode*)malloc(sizeof(BTNode));
B->data = 'B';
B->left = NULL;
B->right = NULL;
BTNode* C = (BTNode*)malloc(sizeof(BTNode));
C->data = 'C';
C->left = NULL;
C->right = NULL;
BTNode* D = (BTNode*)malloc(sizeof(BTNode));
D->data = 'D';
D->left = NULL;
D->right = NULL;
BTNode* E = (BTNode*)malloc(sizeof(BTNode));
E->data = 'E';
E->left = NULL;
E->right = NULL;
A->left = B;
A->right = C;
B->left = D;
B->right = E;
LevelOrder(A);
return 0;
}
3>、核心代码
//层序遍历
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
//1、先把树的根节点入队列
if (root != NULL)
{
QueuePush(&q, root);
}
//2、队列不为空,二叉树的该节点出队列,该节点的两个子树的根节点入队列
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%c ", front->data);
QueuePop(&q);
if (front->left != NULL)
{
QueuePush(&q, front->left);
}
if (front->right != NULL)
{
QueuePush(&q, front->right);
}
}
QueueDestroy(&q);
}
@画图分析
6、求二叉树总结点数
法一:利用全局变量
注意:
1、每次调用TreeSize函数后全局变量size变为第一次传入参数的树的总结点个数,再计算其它树的总结点前要把size重新赋值为0。
2、而且多线程下会出现问题,但不用全局变量可以用指针(传址)的方式解决。
//法一、利用全局变量
int size = 0;
void TreeSize(BTNode* root)
{
if (root == NULL)
{
return;
}
size++;
TreeSize(root->left);
TreeSize(root->right);
}
法二:利用递归返回值
注意,递归为void时,只能重复调用,不能累加或累乘。有返回值时可以累加或累乘等。
int TreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
//可以简化为
//return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
7、求叶子节点的个数
说明:先排除空的,再处理
//求叶子节点的个数
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
8、求二叉树的深度
说明:利用递归返回二叉树的深度
int TreeDepth(BTNode* root)
{
int hl = 0;
int hr = 0;
if (root == NULL)
{
return 0;
}
//和后序遍历有点像,后序遍历是左子树右子树遍历完,然后打印当前节点的数据
//而这里是先计算左子树,右子树的深度,然后比较hl和hr,将深度大的一棵树返回的值+1返回
hl = TreeDepth(root->left);
hr = TreeDepth(root->left);
//比较左子树右子树的深度,将大的数+1返回(+1是因为当前节点也是一层)
return hl > hr ? (hl + 1) : (hr + 1);
}
9、销毁二叉树
说明:使用后续销毁,
1>当传入的参数root在调用销毁函数的函数(main)里是节点,那就可以在销毁函数中用一级指针改变root的值
2>这个参数,如果是指向这棵树的树的节点指针,那销毁函数中用一级指针,root=NULL失效,只能用二级指针。
//销毁二叉树的原则是后序销毁
void TreeDestroy(struct TreeNode* root)
{
if (root == NULL)
return;
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
root = NULL;
}
三、总结
- 表示方法:树的表示可以用孩子表示法、双亲表示法、孩子兄弟表示法,而二叉树一般使用孩子表示法(因为子树少)
- 应用:树可以应用到文件目录,而二叉树是的一种特殊情况。
- 二叉树的存储:一般使用链式结构,完全二叉树可以使用顺序结构(非完全二叉树使用顺序结构会浪费空间)
- 二叉树的遍历:使用前中后序遍历,主要利用了递归的思想。使用层序遍历,主要利用了队列先入先出的思想。
- 二叉树的节点数和深度:求总结点数、叶子节点数、二叉树深度都利用了递归累加的思想。二叉树深度还需要比较才能返回值。
四、习题补充
//结构体
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
1、二叉树是否存在value值
//二叉树value值是否存在
// 查找value节点
// 前序遍历的思想
BTNode* find(BTNode* root, char val) {
// 1、根节点为NULL,返回空
if (root == NULL) {
return NULL;
}
// 2、当前节点的val等于value则,返回该节点
if (root->data == val) {
return root;
}
// 3、当前节点val不等于value进入左子树的根的判断
BTNode* isleft = find(root->left, val);
if (isleft != NULL) {
return isleft;
}
// 4、根和左子树都没有val等于value的节点,开始访问右子树
BTNode* isright = find(root->right, val);
if (isright != NULL) {
return isright;
}
}
2、查找第k层节点个数
// 查找第k层节点个数
int KCount(BTNode* root, int k) {
// 1、如果root=NULL,返回空,没有节点
if (root == NULL) {
return NULL;
}
// 2、
//在这里k相当于一个计数器,每次-1后,就把当前root指向的节点当作第一层
//下面还有k-1层才能到根节点的第k层
//最后k=1时,root指向的节点就是满足 原始根节点第k层的节点
if (k == 1) {
return 1;
}
// 3、如果还没到,就进入递归,寻找对原始根节点来说的第k层的节点
return KCount(root->left,k-1) + KCount(root->right, k - 1);
}
3、翻转二叉树
链接:LeetCode226.翻转二叉树
代码:
// 翻转二叉树
BTNode* invertTree(BTNode* root) {
// 1、判断root是否为空,包含最开始时和访问叶子节点后的空
if (root == NULL) {
return NULL;
}
// 2、交换当前节点的左右子树
struct TreeNode* tmp = root->left;
root->left = root->right;
root->right = tmp;
// 3、进入递归,去交换左右子树
invertTree(root->left);
invertTree(root->right);
return root;
}
4、检查两棵树是否相同
// 检查两棵树是否相同
bool isSameTree(struct BinaryTreeNode* p, struct BinaryTreeNode* q) {
// 1、两棵树都是空
if (p == NULL && q == NULL) {
return true;
}
// 2、两棵树中有一棵为空
else if ((p == NULL && q != NULL) || (p != NULL && q == NULL)) {
return false;
}
// 3、两棵树都非空
else {
//两棵树对应的当前节点val不相等
if (p->data != q->data) {
return false;
}
//值相等时,进入递归,判断左右子树是否都符合相等
isSameTree(p->left, q->left);
isSameTree(p->right, q->right);
}
return true;
}
5、层序遍历(Push和Pop有返回值版)
说明:
先创建一个队列,先把树的根节点入队列
然后队列不空就把队头元素取出,再把这个元素的左右子树的非空的根节点入队列
最后队列为空时结束
// 结构体部分
// 树的部分
typedef char TreeDataType;
typedef struct BinaryTreeNode {
TreeDataType val;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}TreeNode;
// 队列部分
typedef TreeNode QDataType;
//链表的节点
typedef struct QNode
{
QDataType data;
struct QNode* next;
}QNode;
//存储head和tail两个指针,用来连接链表
typedef struct Queue
{
QNode* head;
QNode* tail;
}Queue;
// 队列Push和Pop实现:
//队尾入队(尾插)Push
QNode* QueuePush(Queue* pq, TreeNode x)
{
assert(pq);
//注意1:创建新节点
QNode* newnode = (QNode*)malloc(sizeof(QNode));
//1、空间申请失败
if (newnode == NULL)
{
printf("malloc fail\n");
exit(-1);
}
//2、空间申请成功
newnode->data = x;
newnode->next = NULL;
//注意2:连接链表
//3、处理队列链表头节点
if (pq->head == NULL)
{
pq->head = pq->tail = newnode;
}
//4、处理其它节点
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
return newnode;
}
//队头出队(头删)Pop
QNode* QueuePop(Queue* pq)
{
assert(pq);
//注意1:若队列中没有数据了,就不能出队了,会中止程序
assert(pq->head);
//重点:注意2:要把只有一个节点单独提出来,否则tail始终指向最后一个节点,它变成野指针
if (pq->head->next == NULL)
{
QNode* ret = pq->head;
pq->head = pq->tail = NULL;
return ret;
}
else
{
//注意3:free()前,记录第一个节点的下一个节点
// 有返回值就不需要free
QNode* next = pq->head->next;
QNode* ret = pq->head;
pq->head = next;
return ret;
}
}
// 核心代码
void levelOrder(TreeNode* root) {
// 空树
if (root == NULL) {
return;
}
// 树非空
Queue qu;
// 1、初始化队列
QueueInit(&qu);
// 2、把根节点入队
QueuePush(&qu, root);
// 3、队列不空,则把当前节点队头弹出,打印
//再把这个节点的左右子树的非空根,入队列
while (!QueueEmpty(&qu)) {
TreeNode* out = QueuePop(&qu);
printf("%c ", out->val);
if (out->left != NULL) {
QueuePush(&qu, out->left);
}
if (out->right != NULL) {
QueuePush(&qu, out->right);
}
// 4、释放出队树节点的空间
free(out);
}
// 5、销毁队列
QueueDestroy(&qu);
}