地心地固坐标系(ECEF)与站心坐标系(ENU)的转换
文章目录
- 1. 概述
- 2. 原理
-
- 2.1. 平移
- 2.2. 旋转
- 2.3. 总结
- 3. 实现
- 4. 参考
1. 概述
我在《大地经纬度坐标与地心地固坐标的的转换》这篇文章中已经论述了地心坐标系的概念。我们知道,基于地心坐标系的坐标都是很大的值,这样的值是不太方便进行空间计算的,所以很多时候可以选取一个站心点,将这个很大的值变换成一个较小的值。以图形学的观点来看,地心坐标可以看作是世界坐标,站心坐标可以看作局部坐标。
站心坐标系以一个站心点为坐标原点,当把坐标系定义为X轴指东、Y轴指北,Z轴指天,就是ENU(东北天)站心坐标系。这样,从地心地固坐标系转换成的站心坐标系,就会成为一个符合常人对地理位置认知的局部坐标系。同时,只要站心点位置选的合理(通常可选取地理表达区域的中心点),表达的地理坐标都会是很小的值,非常便于空间计算。
2. 原理
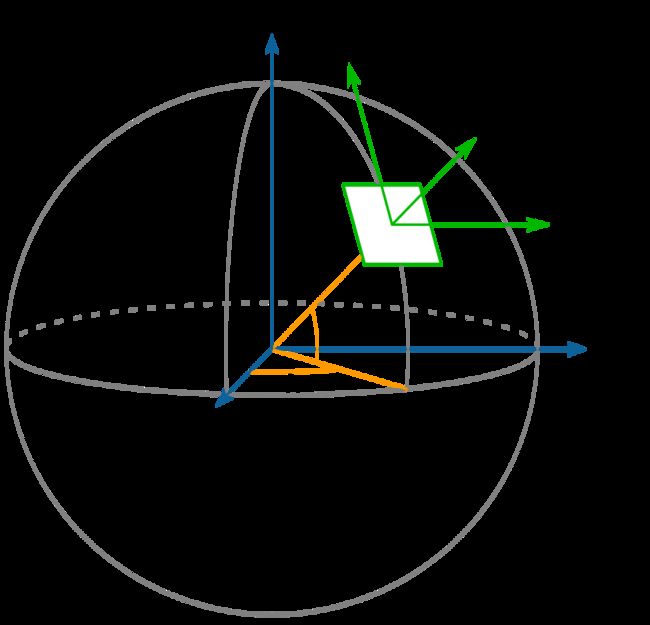
令选取的站心点为P,其大地经纬度坐标为 ( B p , L p , H p ) (B_p,L_p,H_p) (Bp,Lp,Hp),对应的地心地固坐标系为 ( X p , Y p , Z p ) (X_p,Y_p,Z_p) (Xp,Yp,Zp)。地心地固坐标系简称为ECEF,站心坐标系简称为ENU。
2.1. 平移
通过第一节的图可以看出,ENU要转换到ECEF,一个很明显的图形操作是平移变换,将站心移动到地心。根据站心点P在地心坐标系下的坐标 ( X p , Y p , Z p ) (X_p,Y_p,Z_p) (Xp,Yp,Zp),可以很容易推出ENU转到ECEF的平移矩阵:
T = [ 1 0 0 X p 0 1 0 Y p 0 0 1 Z p 0 0 0 1 ] T = \begin{bmatrix} 1&0&0&X_p\\ 0&1&0&Y_p\\ 0&0&1&Z_p\\ 0&0&0&1\\ \end{bmatrix} T=⎣⎢⎢⎡100001000010XpYpZp1⎦⎥⎥⎤
反推之,ECEF转换到ENU的平移矩阵就是T的逆矩阵:
T − 1 = [ 1 0 0 − X p 0 1 0 − Y p 0 0 1 − Z p 0 0 0 1 ] T^{-1} = \begin{bmatrix} 1&0&0&-X_p\\ 0&1&0&-Y_p\\ 0&0&1&-Z_p\\ 0&0&0&1\\ \end{bmatrix} T−1=⎣⎢⎢⎡100001000010−Xp−Yp−Zp1⎦⎥⎥⎤
2.2. 旋转
另外一个需要进行的图形变换是旋转变换,其旋转变换矩阵根据P点所在的经度L和纬度B确定。这个旋转变换有点难以理解,需要一定的空间想象能力,但是可以直接给出如下结论:
- 当从ENU转换到ECEF时,需要先旋转再平移,旋转是先绕X轴旋转 ( p i 2 − B ) (\frac{pi}{2}-B) (2pi−B),再绕Z轴旋转 ( p i 2 + L ) (\frac{pi}{2}+L) (2pi+L)
- 当从ECEF转换到ENU时,需要先平移再旋转,旋转是先绕Z轴旋转 − ( p i 2 + L ) -(\frac{pi}{2}+L) −(2pi+L),再绕X轴旋转 − ( p i 2 − B ) -(\frac{pi}{2}-B) −(2pi−B)
根据我在《WebGL简易教程(五):图形变换(模型、视图、投影变换)》提到的旋转变换,绕X轴旋转矩阵为:
R x = [ 1 0 0 0 0 c o s θ − s i n θ 0 0 s i n θ c o s θ 0 0 0 0 1 ] R_x = \begin{bmatrix} 1&0&0&0\\ 0&cosθ&-sinθ&0\\ 0&sinθ&cosθ&0\\ 0&0&0&1\\ \end{bmatrix} Rx=⎣⎢⎢⎡10000cosθsinθ00−sinθcosθ00001⎦⎥⎥⎤
绕Z轴旋转矩阵为:
R z = [ c o s θ − s i n θ 0 0 s i n θ c o s θ 0 0 0 0 1 0 0 0 0 1 ] R_z = \begin{bmatrix} cosθ&-sinθ&0&0\\ sinθ&cosθ&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} Rz=⎣⎢⎢⎡cosθsinθ00−sinθcosθ0000100001⎦⎥⎥⎤
从ENU转换到ECEF的旋转矩阵为:
R = R z ( p i 2 + L ) ⋅ R x ( p i 2 − B ) (1) R = {R_z(\frac{pi}{2}+L)}\cdot{R_x(\frac{pi}{2}-B)} \tag{1} R=Rz(2pi+L)⋅Rx(2pi−B)(1)
根据三角函数公式:
s i n ( π / 2 + α ) = c o s α s i n ( π / 2 − α ) = c o s α c o s ( π / 2 + α ) = − s i n α c o s ( π / 2 − α ) = s i n α sin(π/2+α)=cosα\\ sin(π/2-α)=cosα\\ cos(π/2+α)=-sinα\\ cos(π/2-α)=sinα\\ sin(π/2+α)=cosαsin(π/2−α)=cosαcos(π/2+α)=−sinαcos(π/2−α)=sinα
有:
R z ( p i 2 + L ) = [ − s i n L − c o s L 0 0 c o s L − s i n L 0 0 0 0 1 0 0 0 0 1 ] (2) R_z(\frac{pi}{2}+L) = \begin{bmatrix} -sinL&-cosL&0&0\\ cosL&-sinL&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} \tag{2} Rz(2pi+L)=⎣⎢⎢⎡−sinLcosL00−cosL−sinL0000100001⎦⎥⎥⎤(2)
R x ( p i 2 − B ) = [ 1 0 0 0 0 s i n B − c o s B 0 0 c o s B s i n B 0 0 0 0 1 ] (3) R_x(\frac{pi}{2}-B) = \begin{bmatrix} 1&0&0&0\\ 0&sinB&-cosB&0\\ 0&cosB&sinB&0\\ 0&0&0&1\\ \end{bmatrix} \tag{3} Rx(2pi−B)=⎣⎢⎢⎡10000sinBcosB00−cosBsinB00001⎦⎥⎥⎤(3)
将(2)、(3)带入(1)中,则有:
R = [ − s i n L − s i n B c o s L c o s B c o s L 0 c o s L − s i n B s i n L c o s B s i n L 0 0 c o s B s i n B 0 0 0 0 1 ] (4) R = \begin{bmatrix} -sinL&-sinBcosL&cosBcosL&0\\ cosL&-sinBsinL&cosBsinL&0\\ 0&cosB&sinB&0\\ 0&0&0&1\\ \end{bmatrix} \tag{4} R=⎣⎢⎢⎡−sinLcosL00−sinBcosL−sinBsinLcosB0cosBcosLcosBsinLsinB00001⎦⎥⎥⎤(4)
而从ECEF转换到ENU的旋转矩阵为:
R − 1 = R x ( − ( p i 2 − B ) ) ⋅ R z ( − ( p i 2 + L ) ) (5) R^{-1} = {R_x(-(\frac{pi}{2}-B))} \cdot {R_z(-(\frac{pi}{2}+L))} \tag{5} R−1=Rx(−(2pi−B))⋅Rz(−(2pi+L))(5)
旋转矩阵是正交矩阵,根据正交矩阵的性质:正交矩阵的逆矩阵等于其转置矩阵,那么可直接得:
R − 1 = [ − s i n L c o s L 0 0 − s i n B c o s L − s i n B s i n L c o s B 0 c o s B c o s L c o s B s i n L s i n B 0 0 0 0 1 ] (6) R^{-1} = \begin{bmatrix} -sinL&cosL&0&0\\ -sinBcosL&-sinBsinL&cosB&0\\ cosBcosL&cosBsinL&sinB&0\\ 0&0&0&1\\ \end{bmatrix} \tag{6} R−1=⎣⎢⎢⎡−sinL−sinBcosLcosBcosL0cosL−sinBsinLcosBsinL00cosBsinB00001⎦⎥⎥⎤(6)
2.3. 总结
将上述公式展开,可得从ENU转换到ECEF的图形变换矩阵为:
M = T ⋅ R = [ 1 0 0 X p 0 1 0 Y p 0 0 1 Z p 0 0 0 1 ] [ − s i n L − s i n B c o s L c o s B c o s L 0 c o s L − s i n B s i n L c o s B s i n L 0 0 c o s B s i n B 0 0 0 0 1 ] M = T \cdot R = \begin{bmatrix} 1&0&0&X_p\\ 0&1&0&Y_p\\ 0&0&1&Z_p\\ 0&0&0&1\\ \end{bmatrix} \begin{bmatrix} -sinL&-sinBcosL&cosBcosL&0\\ cosL&-sinBsinL&cosBsinL&0\\ 0&cosB&sinB&0\\ 0&0&0&1\\ \end{bmatrix} M=T⋅R=⎣⎢⎢⎡100001000010XpYpZp1⎦⎥⎥⎤⎣⎢⎢⎡−sinLcosL00−sinBcosL−sinBsinLcosB0cosBcosLcosBsinLsinB00001⎦⎥⎥⎤
而从ECEF转换到ENU的图形变换矩阵为:
M − 1 = R − 1 ∗ T − 1 = [ − s i n L c o s L 0 0 − s i n B c o s L − s i n B s i n L c o s B 0 c o s B c o s L c o s B s i n L s i n B 0 0 0 0 1 ] [ 1 0 0 − X p 0 1 0 − Y p 0 0 1 − Z p 0 0 0 1 ] M^{-1} = R^{-1} * T^{-1} = \begin{bmatrix} -sinL&cosL&0&0\\ -sinBcosL&-sinBsinL&cosB&0\\ cosBcosL&cosBsinL&sinB&0\\ 0&0&0&1\\ \end{bmatrix} \begin{bmatrix} 1&0&0&-X_p\\ 0&1&0&-Y_p\\ 0&0&1&-Z_p\\ 0&0&0&1\\ \end{bmatrix} M−1=R−1∗T−1=⎣⎢⎢⎡−sinL−sinBcosLcosBcosL0cosL−sinBsinLcosBsinL00cosBsinB00001⎦⎥⎥⎤⎣⎢⎢⎡100001000010−Xp−Yp−Zp1⎦⎥⎥⎤
3. 实现
接下来用代码实现这个坐标转换,选取一个站心点,以这个站心点为原点,获取某个点在这个站心坐标系下的坐标:
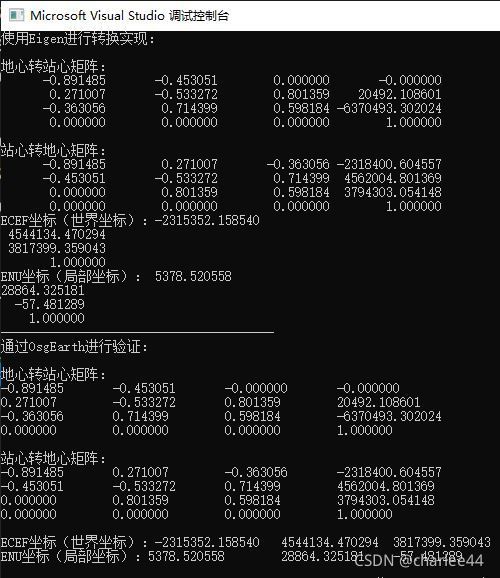
#include 这个示例先用Eigen矩阵库,计算了坐标转换需要的矩阵和转换结果;然后通过osgEarth进行了验证,两者的结果基本一致。运行结果如下:
4. 参考
- 站心坐标系和WGS-84地心地固坐标系相互转换矩阵
- Transformations between ECEF and ENU coordinates
- GPS经纬度坐标WGS84到东北天坐标系ENU的转换
- 三维旋转矩阵;东北天坐标系(ENU);地心地固坐标系(ECEF);大地坐标系(Geodetic);经纬度对应圆弧距离