【c++进阶】二叉搜索树
二叉搜索树
- 一、二叉搜索树概念
- 二、二叉搜索树操作
-
- 2.1 增
- 2.2 删
-
- 2.2.1 非递归
- 2.2.2 递归
- 2.3 查找
- 2.4 拷贝构造
- 2.5 析构
一、二叉搜索树概念
二叉搜索树又称二叉排序树,他或者是一棵空树,或者是具有一下性质的二叉树
- 若他的左子树不为空,则左子树上所有结点的值都小于根结点的值。
- 若他的右子树不为空,则右子树上所有结点的值都大于根结点的值。
- 他的左右子树也分别为二叉搜索树。
二、二叉搜索树操作
我们需要一个BSTreeNode的结构体
template <class k>
struct BSTreeNode
{
BSTreeNode<k>* _left;
BSTreeNode<k>* _right;
k _key;
BSTreeNode(const k& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
还有其他的
template <class k>
class BSTree
{
typedef BSTreeNode<k> Node;
private:
Node* _root = nullptr;
}
2.1 增
- 非递归
插入的思想就是先去比较,比cur大就往右边走,比cur小就往左边走,然后再链接。
我们可以看到当cur=new Node(key)后,怎么链接起来成了问题,
因为我们无法找到cur的父节点,所以在cur每一次往下走之前,先记录好此时cur的位置,也就是往下走之后的cur的父节点
bool Insert(const k& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if(cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
//链接
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
- 递归
插入也可以用递归的方法来写。大致的思想差不多但是有些要注意的地方,先看下列代码。
bool _InsertR(Node*& root, const k& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
递归法的重点就在于Node*
&root,因为加了引用,所以每一次root的值就可以得到修改,父与子的链接关系也不需要别的操作。
2.2 删
2.2.1 非递归
删除要分为三种情况(要删除的结点是cur):
-
cur没有孩子。
直接删除。
-
cur的左为空或者右为空。
让cur的父亲领养。
//删除
//左为空
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
//判断cur是在父节点的左边还是右边,方便链接
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
//2.右为空
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
- cur的两边都不为空。
找保姆。
因为搜索二叉树的特性,根的左节点比它小,根的右节点比它大。
所以我们有两种方案
1.右树的最小节点替代
2.左树的最大节点替代
这里以右树的最小节点为例
(1) 定义pminRight和minRight,先找到cur(要删除的节点)的右树,即minRight=cur->_right
(2)开始走循环,找到右树的最小节点,并用pminRight记录minRight往下走之前的位置(走到最后就是记录了minRight的父亲)方便后面链接。
(3)找到了右树最小节点,因为要让它当保姆领养被删除的节点的孩子,所以,将两个位置的内容互换,然后pminRight与右树最小节点的孩子链接,删除右树最小节点。
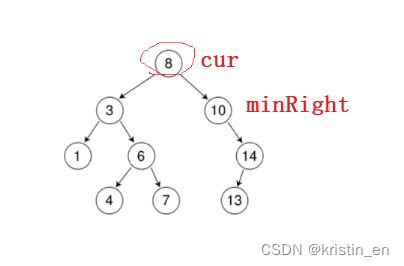
对照着图理解完之后,就有了接下来的代码

这种写法是错误的,错误已经表明了,有两处错误。
所以应该使pminRight=cur,这样不会导致空指针的解引用。然后在链接处应该像插入一样判断位置。
else
{
//找右树最小结点代替,也可以是左树最大结点代替
Node* pminRight = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
pminRight = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
//链接
if (pminRight->_left == minRight)
{
pminRight->_left = minRight->_right;
}
else
{
pminRight->_right = minRight->_right;
}
delete minRight;
}
附上完整代码
bool Erase(const k & key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
//删除
//左为空
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
//2.右为空
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
//找右树最小结点代替,也可以是左树最大结点代替
Node* pminRight = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
pminRight = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
//链接
if (pminRight->_left == minRight)
{
pminRight->_left = minRight->_right;
}
else
{
pminRight->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
}
2.2.2 递归
bool _EraseR(Node*& root, const k& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else//找到了,链接
{
Node* del = root;
//删除
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* maxleft = root->_left;
while (maxleft->_right)
{
maxleft = maxleft->_right;
}
swap(root->_key, maxleft->left);
return _EraseR(root->_left, key);
}
delete del;
return true;
}
}
2.3 查找
key比根小走左边,比根大走右边,找到了返回true,找不到返回false。
bool Find(const k& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
递归实现
找到了返回true,root==nullptr返回false,key大于根递归右子树,key小于根递归左子树。
bool _FindR(Node* root, const k& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key == key)
{
return true;
}
if (root->_key < key)
return _FindR(root->_right, key);
else
return _FindR(root->left, key);
}
2.4 拷贝构造
将这棵树复制一遍(深拷贝)。
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newNode = new Node(root->_key);
newNode->_left = Copy(root->_left);
newNode->_right = Copy(root->_right);
return newNode;
}
2.5 析构
~BSTree()
{
Destroy(_root);
}
void Destroy(Node*& root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}


