Robust data-driven state-feedback design 论文阅读
Robust data-driven state-feedback design 论文阅读
- 原文翻译
-
- 摘要
- 一、介绍
- 二、准备工作
- 三、 数据驱动状态反馈
-
- A.不确定闭环参数化
- 引用
原文翻译
摘要
我们考虑以下问题:直接基于测量数据设计离散时间线性时不变系统的鲁棒状态反馈控制器。所提出的控制器设计程序不需要模型知识,只需要可能会受到噪声影响的单个开环数据轨迹。
首先,推导了一类不确定闭环矩阵在状态反馈下的数据驱动特征。通过在鲁棒控制框架中考虑这种参数化,我们设计了具有稳定性和性能保证的数据驱动状态反馈增益,包括例如H∞-控制问题作为一种特殊情况。此外,我们展示了如何扩展所提出的框架以考虑部分模型知识。通过数值算例说明了该方法的有效性。
一、介绍
最近,直接根据测量数据设计控制器受到越来越多的关注[1],[2]。虽然已建立的方法(例如,基于强化学习的方法)很少解决闭环保证问题,但人们重新努力使用新的统计估计技术[3]、[4]、[5]、[6]提供这种保证。潜在的替代方案是,例如,具有先验集成员身份识别的鲁棒控制[7],这是众所周知的计算要求高的,以及基于反伪的方法[8],这通常需要无限长的数据来实现闭环保证。一般来说,即使数据由线性时不变(LTI)系统生成,使用有限长度的噪声数据为闭环提供非保守端到端保证也是一个开放问题。
实现这一目标的一种有希望的方法依赖于行为系统理论。在[9]中,证明了LTI系统(线性实不变系
统)的所有输入-输出轨迹的向量空间由单个测量轨迹的时移跨越,假设各个输入信号持续激励。因此,可以使用单个数据轨迹来表征LTI系统,而无需任何先前的识别步骤。最近,在数据驱动系统分析和控制的背景下,有各种贡献考虑了这一结果,包括测量数据的耗散性验证[10]或者将[9]推广到某些非线性系统[11]。此外,最近的工作[12]导出了状态反馈下LTI系统的简单数据相关闭环参数化。该参数化用于从数据中解决各种控制问题,包括稳定和线性二次调节。然而,在存在噪声数据的情况下,没有给出有意义的保证。
本文的目标是为数据驱动控制提供非保守的端到端保证。更准确地说,我们使用有限长度的单噪声输入状态轨迹来设计控制器,以保证所有系统的闭环稳定性和性能,这些系统与测量数据和假定的噪声边界一致。这是通过扩展[12]的方法以考虑噪声并将鲁棒控制技术应用于所产生的不确定系统类别来实现的。最近的另一篇论文[13]考虑了数据驱动的分析和控制,其中没有持续令人兴奋的数据。特别是,对于无噪声数据,即使不能唯一地识别系统,也可以从数据中解决某些控制问题,从而说明了直接数据驱动控制的优点。类似地,本文的结果不需要明确的激励持续性。此外,我们的结果导致了具有理想闭环保证的直接数据驱动控制的简单设计过程,因此是基于辨识的控制的一种有希望的替代方案。
论文结构:首先在第二节中陈述问题公式,并使用噪声数据来描述状态反馈下的不确定闭环。其次在第三节中应用已知的鲁棒控制方法来设计具有稳定性和性能保证的控制器。此外,我们将所提出的纯数据驱动方法扩展到具有混合数据驱动和基于模型的组件的系统。在第四节中,我们成功地将鲁棒状态反馈设计技术应用于不稳定示例系统。论文在第五节结束。
二、准备工作
我们用 I n I_n In表示 n × n n \times n n×n单位矩阵,其中如果维度与上下文无关,则省略索引 n n n。
进一步用 A ⊥ A^\bot A⊥ 表示包含a的核的基的矩阵。我们用 L 2 \mathcal L_2 L2表示平方可和序列空间。在线性矩阵不等式(LMI)中, ∗ * ∗表示可以从对称性推断的块。此外,对于一个元素为 { x k } k = i i + L + N − 2 \{x_k\}_{k=i}^{i+L+N−2} {xk}k=ii+L+N−2的序列 x x x的汉克尔矩阵定义为:

也就是说,矩阵 X i , L N X_{i,L}^N Xi,LN从元素 x i x_i xi开始,有 L L L行和 N N N列。作为速记符号,我们将 x x x的 N N N个窗口缩写为,分别由从 i = 0 i=0 i=0和 i = 1 i=1 i=1开始的序列
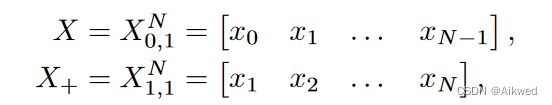
在本文中,我们考虑以下形式的LTI系统:

其中 x k ∈ R n x_k \in \R_n xk∈Rn是状态, w k ∈ R m w w_k \in \R^{m_w} wk∈Rmw是干扰, u k ∈ R m u_k \in \R^m uk∈Rm是控制输入, Z k ∈ R p z Z_k \in \R^{p_z} Zk∈Rpz是性能输出。我们设计了状态反馈控制器 u k = K x k u_k = Kx_k uk=Kxk来控制系统(1)。我们的设计程序是纯数据驱动的,不需要真正的系统矩阵 A t r A_tr Atr, B t r B_tr Btr的知识。
然而,我们确实假设矩阵 B w , C , D w , D B_w,C,D_w,D Bw,C,Dw,D是已知的。出于我们的目的, B w B_w Bw本质上是一个参数,用于模拟干扰的影响,而 C , D w , D C,Dw,D C,Dw,D构成了用户对性能的选择。在本文中,我们使用下面的定义所考虑的数据的持续激励。
定义 1.
如果矩阵 [ X U ] \begin{bmatrix}X \\U \\ \end{bmatrix} [XU]行满秩,则序列 { x k , u k } k = 0 N − 1 \{x_k,u_k\}_{k=0}^{N−1} {xk,uk}k=0N−1被称为为持续激励。
根据[9],输入的可控性和一定的秩性足以使激励持续。
定理 2 ([9, 推论 2])
如果 ( A t r , [ B t r − B w ] ( A_{tr},[B_{tr}-B_w ] (Atr,[Btr−Bw]可控,且矩阵:
[ W 0 , n + 1 N − n U 0 , n + 1 N − n ] \begin{bmatrix} W_{0,n+1}^{N-n}\\ U_{0,n+1}^{N-n}\\ \end{bmatrix} [W0,n+1N−nU0,n+1N−n]行满秩,则 { x k , u k } k = 0 N − 1 \{x_k,u_k\}_{k=0}^{N−1} {xk,uk}k=0N−1是持续的激励。
定义1不同于[9]中所考虑的激励持续性的概念,该概念仅涉及输入数据,并且为了方便起见,在本文中是优选的。在[12]中,显示了如何使用单个持续激励开环轨迹来恢复LTI系统的系统矩阵。此外,还导出了状态反馈下闭环的线性参数化,这也仅取决于单个开环数据轨迹。本论文的贡献在于扩展[12]的框架,以便在存在噪声的情况下提供鲁棒稳定性和性能保证。与[12]相反,我们的结果通常不需要持续的激励。
在本文中,我们考虑以下场景:从仿真或实验中,对于某些未知干扰 { w ^ k } k = 0 N − 1 \{\hat w_k\}_{k=0}^{N-1} {w^k}k=0N−1,可以得到一个单开环输入状态序列 { x k , u k } k = 0 N \{x_k,u_k\}_{k=0}^N {xk,uk}k=0N 作为(1)的轨迹。该轨迹直接用于鲁棒控制器设计,无需事先进行系统辨识。关于干扰实现的唯一可用信息是如下矩阵上的跟随边界

假设3 矩阵 W ^ \hat W W^是下列集合的元素

对于一些已知的矩阵 Q w ∈ R m w × m w Q_w \in \R ^ {m_w \times m_w} Qw∈Rmw×mw, S w ∈ R m w × N S_w \in \R ^ {m_w \times N} Sw∈Rmw×N, R w ∈ R N × N R_w \in \R ^ {N \times N} Rw∈RN×N, 0 ≺ R w 0 \prec R_w 0≺Rw。
通过假设3,假设影响测量数据的未知扰动实现位于由二次矩阵不等式描述的某个已知集合中。隐含地, W ^ ∈ W \hat W \in \mathcal W W^∈W表示序列 { w ^ k } k = 0 N − 1 \{\hat w_k \}_{k = 0}^{N-1} {w^k}k=0N−1上的二次界,并且作为特殊情况包含许多实际边界。
例如,如果 w ^ \hat w w^的最大奇异值有界为 σ m a x ( W ^ ) ≤ w ˉ \sigma_{max}(\hat W)\le \bar w σmax(W^)≤wˉ,然后是 w ^ ∈ W \hat w \in W w^∈W适用于 Q w = − I , S w = 0 , R w = w ˉ 2 I Q_w=-I,S_w=0,R_w= \bar w^2I Qw=−I,Sw=0,Rw=wˉ2I。
更一般地,对形式 W ^ ∈ W \hat W \in W W^∈W提供了一个灵活的框架来建模一般噪声信号,特别是当组合多个二次矩阵不等式时。
对于未来的研究来说,为不同的实际相关场景(如序列 { w ^ k } k = 0 N − 1 \{ \hat w_k\}_{k=0}^{N-1} {w^k}k=0N−1的范数边界)导出合适的矩阵 Q w , S w , R w Q_w,S_w,R_w Qw,Sw,Rw是一个有趣的方面。
三、 数据驱动状态反馈
在本节中,我们考虑状态反馈增益的设计,直接基于被满足假设3的扰动扰动的测量数据。首先,我们利用单一开环数据轨迹推导出不确定闭环的数据驱动特性。然后,我们将已知的鲁棒控制方法应用到该参数化中,以设计状态反馈控制器,保证所有闭环矩阵的稳定性和性能与测量数据一致。最后,我们将提出的框架扩展到混合了数据驱动和基于模型的组件的系统。
A.不确定闭环参数化
在下文中,我们通过使用噪声测量表征(1)在状态反馈下的闭环动力学来扩展[12]。设 { x k , u k } k = 0 N \{x_k,u_k\}_{k=0}^N {xk,uk}k=0N是(1)的测量轨迹,设{xk,uk}Nk=0是(1)的测量轨迹,对应于未知扰动实现ˆW。
引用
[1] Z.-S. Hou and Z. Wang, “From model-based control to data-driven control: Survey,classification and perspective,” Information Sciences,vol. 235, pp. 3–35, 2013,
[2] B. Recht, “A tour of reinforcement learning: The view from continuous control,” Annual Review of Control, Robotics, and AutonomousSystems, 2018.
[3] N. Matni and S. Tu, “A tutorial on concentration bounds for system identification,” arXiv preprint arXiv:1906.11395, 2019.
[4] N. Matni, A. Proutiere, A. Rantzer, and S. Tu, “From self-tuning regulators to reinforcement learning and back again,” arXiv preprint arXiv:1906.11392, 2019.
[5] R. Boczar, N. Matni, and B. Recht, “Finite-data performance guarantees for the output-feedback control of an unknown system,” in Proc.57th IEEE Conf. on Decision and Control, 2018, pp. 2994–2999.
[6] S. Dean, H. Mania, N. Matni, B. Recht, and S. Tu, “On the sample complexity of the linear quadratic regulator,” F oundations of Computa-tional Mathematics, 2019, https://doi.org/10.1007/s10208-019-09426-y.
[7] M. Milanese and A. Vicino, “Optimal estimation theory for dynamic systems with set membership uncertainty: an overview,” Automatica,vol. 27, no. 6, pp. 997–1009, 1991.
[8] R. L. Kosut, “Uncertainty model unfalsification for robust adaptive control,” Annual Reviews in Control, vol. 25, pp. 65–76, 2001.
[9] J. C. Willems, P . Rapisarda, I. Markovsky, and B. De Moor, “A note on persistency of excitation,” Systems & Control Letters, vol. 54, pp.325–329, 2005.
[10] A. Romer, J. Berberich, J. Köhler, and F. Allgöwer, “One-shot verification of dissipativity properties from input-output data,” IEEE Control Systems Letters, vol. 3, no. 3, pp. 709–714, 2019.
[11] J. Berberich and F. Allgöwer, “A trajectory-based framework for data-driven system analysis and control,” in Proc. European Control Conference, 2020, to appear, preprint online: arXiv:1903.10723.
[12] C. De Persis and P . Tesi, “Formulas for data-driven control: Stabilization, optimality and robustness,” arXiv:1903.06842, 2019.
[13] H. J. van Waarde, J. Eising, H. L. Trentelman, and M. K. Camlibel,“Data informativity: a new perspective on data-driven system analysis and control,” arXiv:1908.00468, 2019.
[14] K. Zhou, J. C. Doyle, and K. Glover, Robust and optimal control.Prentice-Hall, Inc., Englewood Cliffs, N.J., 1996.
[15] C. Scherer and S. Weiland, Linear Matrix Inequalities in Control,3rd ed. New Y ork: Springer-V erlag, 2000.
[16] C. Scherer, “Robust mixed control and linear parameter-varying control with full-block scalings,” in Advances in Linear Matrix Inequality Methods in Control. SIAM: Philadelphia, 2000, pp. 187–207.
[17] M. G. Safonov and T.-C. Taso, “The unfalsified control concept and learning,” IEEE Transactions on Automatic Control, vol. 42, no. 6, pp.843–847, 1997.