OFDM——PAPR减小
文章目录
- 前言
- 一、PAPR 减小
- 二、MATLAB 仿真
-
- 1、OFDM 信号的 CCDF
-
- ①、MATLAB 源码
- ②、仿真结果
- 2、单载波基带/通频带信号的 PAPR
-
- ①、MATLAB 源码
- ②、仿真结果
- 3、时域 OFDM 信号和幅度分布
-
- ①、MATLAB 源码
- ②、仿真结果
- 4、Chu 序列和 IEEE802.16e 前导的 PAPR
-
- ①、MATLAB 源码
- ②、仿真结果
-
- 1) Chu 序列经 IFFT 之后的幅度
- 2) IEEE 802.16e 前导的 PAPR
- 5、基于限幅和滤波的 OFDM 信号
-
- ①、MATLAB 源码
- ②、仿真结果
-
- 1)基带信号及通频带信号功率谱、PDF、功率
- 2)限幅信号、滤波信号的 PDF 和功率谱
- 3)等波纹通频带 FIR 滤波器的特点
- 6、采用限幅和滤波后的 PAPR 分布和 BER 性能
- 7、部分传输序列(PTS)
- 8、DFT 扩频
- 9、采用脉冲成型的 DFT 扩频的 PAPR 分析
- 三、资源自取
前言
本文对减小 OFDM 峰值平均功率比(PAPR—Peak to Average Power Ratio)的内容以思维导图的形式呈现,有关仿真部分进行了讲解实现。
一、PAPR 减小
减小 OFDM 峰值平均功率比思维导图如下图所示,如有需求请到文章末尾端自取。

二、MATLAB 仿真
1、OFDM 信号的 CCDF
互补累积分布函数(CCDF,CF超过Z的概率):
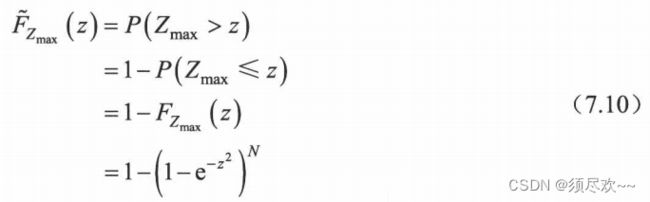
简化了的 累积分布函数(CDF,CF未超过Z的概率):

![]()
①、MATLAB 源码
mapper.m
function [modulated_symbols,Mod] = mapper(b,N)
% If N is given, it generates a block of N random 2^b-PSK/QAM modulated symbols.
% Otherwise, it generates a block of 2^b-PSK/QAM modulated symbols for [0:2^b-1].
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
M=2^b; % Modulation order or Alphabet (Symbol) size
if b==1, Mod='BPSK'; A=1; mod_object=comm.PSKModulator('ModulationOrder', M);
elseif b==2, Mod='QPSK'; A=1;
mod_object = comm.PSKModulator('ModulationOrder', M, 'PhaseOffset', pi/4);
else Mod=[num2str(2^b) 'QAM']; Es=1; A=sqrt(3/2/(M-1)*Es);
mod_object = comm.RectangularQAMModulator('ModulationOrder', M, 'SymbolMapping', 'Gray');
end
if nargin==2 % generates a block of N random 2^b-PSK/QAM modulated symbols
modulated_symbols = A * mod_object(randi([0 M-1], N, 1));
else
modulated_symbols = A * mod_object((0:M-1)');
end
PAPR.m
function [PAPR_dB, AvgP_dB, PeakP_dB] = PAPR(x)
% PAPR_dB : PAPR[dB]
% AvgP_dB : Average power[dB]
% PeakP_dB : Maximum power[dB]
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
Nx=length(x); xI=real(x); xQ=imag(x);
Power = xI.*xI + xQ.*xQ;
PeakP = max(Power); PeakP_dB = 10*log10(PeakP);
AvgP = sum(Power)/Nx; AvgP_dB = 10*log10(AvgP);
PAPR_dB = 10*log10(PeakP/AvgP);
plot_CCDF.m
% plot_CCDF.m
% Plot the CCDF curves of Fig. 7.3.
clear all; clc; clf
Ns = 2.^[6:10]; % OFDM系统中的子载波数量
b=2; % 指定每个符号的比特数
M=2^b; % 根据 b 计算调制阶数
Nblk = 1e3; % 设置仿真的块数
%mod_object = modem.qammod('M',M, 'SymbolOrder','gray');
%Es=1; A=sqrt(3/2/(M-1)*Es);
zdBs = [4:0.1:10];
N_zdBs = length(zdBs);
%Ray_fnc = inline('z/s2*exp(-z^2/(2*s2))','s2','z');
CCDF_formula=inline('1-((1-exp(-z.^2/(2*s2))).^N)','N','s2','z'); % Eq.(7.9) % 代码使用内联函数 inline 定义了函数 CCDF_formula
for n = 1:length(Ns) % 循环遍历 Ns 中的值
N=Ns(n); % 设置当前的子载波数量
x = zeros(Nblk,N); % 初始化一个数组 x,用于存储OFDM时域信号
sqN=sqrt(N); % 计算 N 的平方根
for k = 1:Nblk % 进行 OFDM 块的仿真
%msgint=randint(1,N,M); X=A*modulate(mod_object,msgint);
X = mapper(b,N); % 使用 QPSK 调制方案生成 N 个调制符号
x(k,:) = ifft(X,N)*sqN; % 对 X 执行逆快速傅里叶变换(IFFT),并乘以 sqN 进行能量归一化
CFx(k) = PAPR(x(k,:)); % 计算时域信号 x 的峰均比(PAPR)
end
s2 = mean(mean(abs(x)))^2/(pi/2); % 计算时域信号 x 的平均功率以估计方差 s2。
% 使用 CCDF_formula 函数和 PAPR 值计算理论和仿真的 CCDF 值
CCDF_theoretical=CCDF_formula(N,s2,10.^(zdBs/20)); % 使用公式 Eq.(7.9) 中指定的参数 N、s2 和 zdBs 计算理论 CCDF
for i = 1:N_zdBs
%zdB=zdBs(i); %z=10^(zdB/20); %CCDF_theoretical(i)=CCDF_formula(N,s2,z);
CCDF_simulated(i) = sum(CFx>zdBs(i))/Nblk; % 通过计数大于阈值 zdBs(i) 的 PAPR 值的数量并将其除以总块数 Nblk,估计仿真的 CCDF
end
semilogy(zdBs,CCDF_theoretical,'k-'); hold on; grid on; % 使用对数坐标绘制理论 CCDF 曲线
semilogy(zdBs(1:3:end),CCDF_simulated(1:3:end),'k:*'); % 使用对数坐标绘制仿真 CCDF 曲线
end
axis([zdBs([1 end]) 1e-2 1]);
title('OFDM system with N-point FFT');
xlabel('PAPR0[dB]');
ylabel('CCDF=Probability(PAPR>PAPR0)');
legend('Theoretical','Simulated');
②、仿真结果
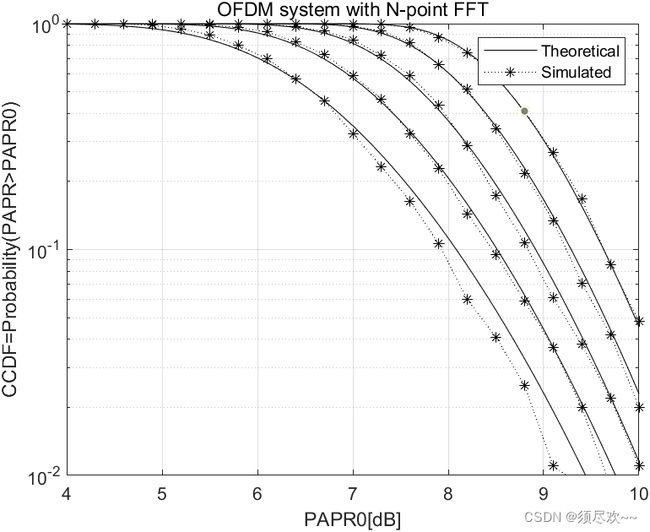
上图显示了当 N = 64,128,256,512,1024 时,OFDM 信号的理论 CCDF 和仿真 CCDF,当 N 变小时,仿真结果偏离理论值,这说明只有 N 足够大时,式(7.11)才是精确的。
2、单载波基带/通频带信号的 PAPR
①、MATLAB 源码
mapper.m
function [modulated_symbols,Mod] = mapper(b,N)
% If N is given, it generates a block of N random 2^b-PSK/QAM modulated symbols.
% Otherwise, it generates a block of 2^b-PSK/QAM modulated symbols for [0:2^b-1].
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
M=2^b; % Modulation order or Alphabet (Symbol) size
if b==1, Mod='BPSK'; A=1; mod_object=comm.PSKModulator('ModulationOrder', M);
elseif b==2, Mod='QPSK'; A=1;
mod_object = comm.PSKModulator('ModulationOrder', M, 'PhaseOffset', pi/4);
else Mod=[num2str(2^b) 'QAM']; Es=1; A=sqrt(3/2/(M-1)*Es);
mod_object = comm.RectangularQAMModulator('ModulationOrder', M, 'SymbolMapping', 'Gray');
end
if nargin==2 % generates a block of N random 2^b-PSK/QAM modulated symbols
modulated_symbols = A * mod_object(randi([0 M-1], N, 1));
else
modulated_symbols = A * mod_object((0:M-1)');
end
modulation.m
function [s,time] = modulation(x,Ts,Nos,Fc)
% Ts : Sampling period
% Nos: Oversampling factor
% Fc : Carrier frequency
Nx=length(x); offset = 0;
if nargin<5
scale = 1;
T=Ts/Nos; % Scale and Oversampling period for Baseband
else
scale = sqrt(2);
T=1/Fc/2/Nos; % Scale and Oversampling period for Passband
end
t_Ts = [0:T:Ts-T];
time = [0:T:Nx*Ts-T]; % One sampling interval and whole interval
tmp = 2*pi*Fc*t_Ts+offset;
len_Ts=length(t_Ts);
cos_wct = cos(tmp)*scale;
sin_wct = sin(tmp)*scale;
%s = zeros(N*len_Ts,1);
for n = 1:Nx
s((n-1)*len_Ts+1:n*len_Ts) = real(x(n))*cos_wct-imag(x(n))*sin_wct;
end
PAPR.m
function [PAPR_dB, AvgP_dB, PeakP_dB] = PAPR(x)
% PAPR_dB : PAPR[dB]
% AvgP_dB : Average power[dB]
% PeakP_dB : Maximum power[dB]
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
Nx=length(x); xI=real(x); xQ=imag(x);
Power = xI.*xI + xQ.*xQ;
PeakP = max(Power); PeakP_dB = 10*log10(PeakP);
AvgP = sum(Power)/Nx; AvgP_dB = 10*log10(AvgP);
PAPR_dB = 10*log10(PeakP/AvgP);
single_carrier_PAPR.m
%%%%%%%%%%%%%%%%%%%%% 计算单载波基带/通频带信号的PAPR %%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%% single_carrier_PAPR.m %%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%程序说明
%%%%分析单载波下的PAPR,可画出图
%%%%%% 仿真环境
%软件版本:MATLAB R2019a
clear
Ts = 1; % 采样时间间隔
L = 8; % 每个符号的采样点数
Nos = 8; % 过采样因子
Fc = 1; % 载波频率
b = 2; % 比特数
M = 2^b; % 调制方案中的符号数
[X,Mod] = mapper(b); % 返回一个长度为 M 的复数向量 X,表示调制方案的符号集合;Mod 表示调制方案的名称
L_ = L*4;
i_b = 1;
[xt_pass_,time_] = modulation(X,Ts,L_,Fc); % 执行连续时间调制
[xt_pass,time] = modulation(X,Ts,L,Fc); % 执行过采样调制:
for i_s = 1:M
xt_base(L*(i_s-1)+1 : L*i_s) = X(i_s)*ones(1,L); % 生成基带信号
end
PAPR_dB_base = PAPR(xt_base); % 计算基带信号的 PAPR
figure(1);
% clf;
subplot(311);
stem(time,real(xt_base),'k.'); % 绘制离散时间信号的实部
hold on;
ylabel('S_{I}(n)');
%title([Mod ', ' num2str(M) ' symbols, Ts=' num2str(Ts) 's, Fs=' num2str(1/Ts*2*Nos) 'Hz, Nos=' num2str(Nos) ', baseband, g(n)=u(n)-u(n-Ts)']);
subplot(312);
stem(time,imag(xt_base),'k.'); % 绘制离散时间信号的虚部
hold on;
ylabel('S_{Q}(n)');
subplot(313);
stem(time,abs(xt_base).^2,'k.'); % 绘制离散时间信号的幅度平方
hold on;
title(['PAPR = ' num2str(round(PAPR_dB_base(i_b)*100)/100) 'dB']);
xlabel ('samples');
ylabel('|S_{I}(n)|^{2}+|S_{Q}(n)|^{2}');
figure(2);
clf;
PAPR_dB_pass(i_b) = PAPR(xt_pass);
subplot(211);
stem(time,xt_pass,'k.');
hold on;
plot(time_,xt_pass_,'k:');
title([Mod ', ' num2str(M) ' symbols, Ts=' num2str(Ts) 's, Fs=' num2str(1/Ts*2*Nos) 'Hz, Nos=' num2str(Nos) ', Fc=' num2str(Fc) 'Hz, g(n)=u(n)-u(n-Ts)']);
ylabel('S(n)');
subplot(212)
stem(time,xt_pass.*xt_pass,'r.');
hold on;
plot(time_,xt_pass_.*xt_pass_,'k:');
title(['PAPR = ' num2str(round(PAPR_dB_pass(i_b)*100)/100) 'dB']);
xlabel('samples');
ylabel('|S(n)|^{2}');
%bb_I = zeros(1,M*Nos*2); bb_Q = zeros(1,M*Nos*2);
disp('PAPRs of baseband/passband signals');
PAPRs_of_baseband_passband_signals=[PAPR_dB_base; PAPR_dB_pass]
②、仿真结果
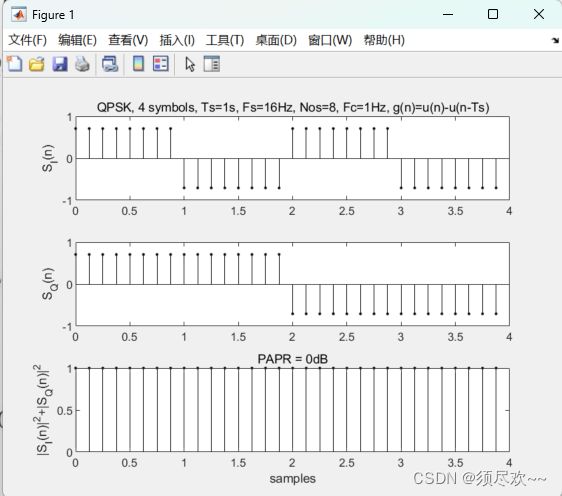
基带信号的平均功率和峰值功率相同,因此它的 PAPR 是 0dB
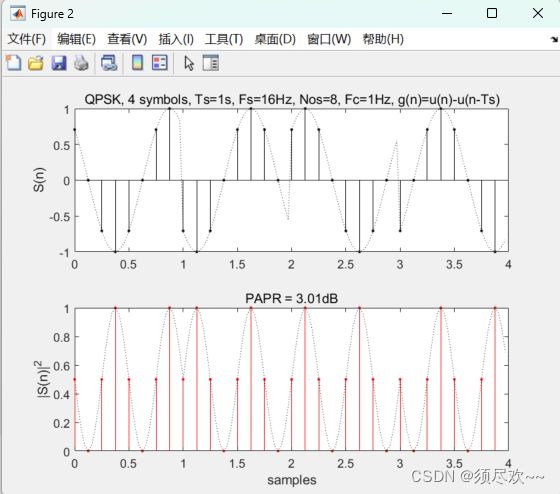
通频带信号的 PAPR 是 3.01dB
注意:单载波信号的 PAPR 随载波频率 f c f_c fc 的变化而变化,因此,为了准确测量单载波系统的 PAPR,必须考虑通频带信号的载波频率。总之,单载波系统的 PAPR 可以由调制方案直接预测,而且不会很大,这与 OFDM 系统不同。
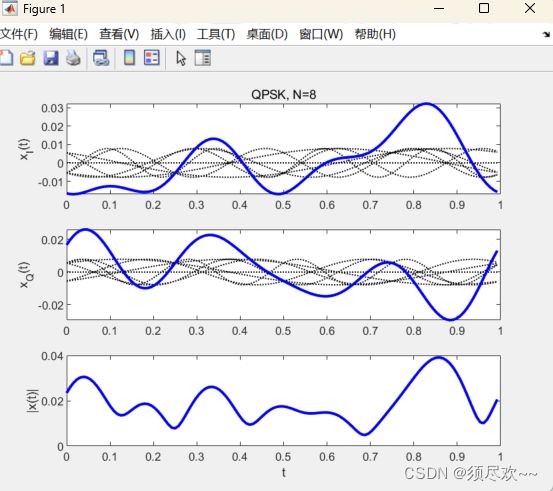
3、时域 OFDM 信号和幅度分布
①、MATLAB 源码
% OFDM_signal.m
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
clear all; clc; clf;
N=8; % 子载波数量
b=2; % 每个子载波的比特数
M=2^b; % 每个子载波的调制阶数
Nos=16; % 每个OFDM符号中的子载波数量
NNos=N*Nos; % 总的子载波数量
T=1/NNos; % 每个OFDM符号的持续时间
time = [0:T:1-T]; % 时间序列,从0到1,步长为T
[X,Mod] = mapper(b,N); % 返回已调制符号X和调制方式Mod
X(1)=0+1i*0; % A block of 16 QPSK symbols with no DC-subcarrier
% 使用ifft函数生成OFDM符号x。根据子载波的索引i,分为两个分支,分别对应于前N/2个子载波和后N/2个子载波。根据索引i和NNos的值,使用ifft函数生成不同的输入序列x。
for i = 1:N
if i<=N/2, x = ifft([zeros(1,i-1) X(i) zeros(1,NNos-i+1)],NNos);
else x = ifft([zeros(1,NNos-N+i-1) X(i) zeros(1,N-i)],NNos);
end
xI(i,:) = real(x); xQ(i,:) = imag(x);
end
sum_xI = sum(xI); sum_xQ = sum(xQ);
figure(1), clf, subplot(311)
plot(time,xI,'k:','linewidth',1),hold on, plot(time,sum_xI,'b','linewidth',2)
title([Mod ', N=' num2str(N)]); ylabel('x_{I}(t)'); axis([0 1 min(sum_xI) max(sum_xI)]);
subplot(312)
plot(time,xQ,'k:','linewidth',1); hold on, plot(time,sum_xQ,'b','linewidth',2)
ylabel('x_{Q}(t)'); axis([0 1 min(sum_xQ) max(sum_xQ)]);
subplot(313), plot(time,abs(sum_xI+j*sum_xQ),'b','linewidth',2); hold on;
ylabel('|x(t)|'); xlabel('t');
clear('xI'), clear('xQ')
N=2^4; NNos=N*Nos; T=1/NNos; time=[0:T:1-T];
Nhist=1e3; % 历史记录数
for k = 1:Nhist
[X,Mod] = mapper(b,N); X(1)=0+j*0; % A block of 16 QPSK symbols with no DC-subcarrier
for i = 1:N
if (i<= N/2) x = ifft([zeros(1,i-1) X(i) zeros(1,NNos-i+1)],NNos);
else x = ifft([zeros(1,NNos-N/2+i-N/2-1) X(i) zeros(1,N-i)],NNos);
end
xI(i,:) = real(x); xQ(i,:) = imag(x);
end
HistI(NNos*(k-1)+1:NNos*k) = sum(xI); HistQ(NNos*(k-1)+1:NNos*k) = sum(xQ); % 将xI和xQ的总和保存在矩阵HistI和HistQ中
end
N_bin = 30;
figure(2), clf, subplot(311)
[xI_dist,bins] = hist(HistI,N_bin); bar(bins,xI_dist/sum(xI_dist),'k'); %#ok②、仿真结果
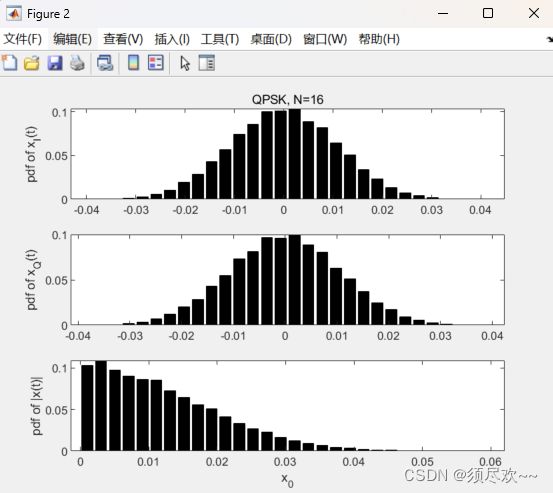
从图中可以看出, x [ n ] x[n] x[n] 的实部和虚部服从高斯分布,而 ∣ x [ n ] ∣ |x[n]| ∣x[n]∣ 或 ∣ x [ t ] ∣ |x[t]| ∣x[t]∣ 服从瑞利分布
对于具有 N 个子载波的OFDM符号,当每个子载波分量具有相同的相位,且恰好出现最大幅度时, OFDM 信号具有最大功率。最大功率随着 N 的增大而增大,而且出现最大功率的概率随着 N 的增大而降低。
4、Chu 序列和 IEEE802.16e 前导的 PAPR
①、MATLAB 源码
PAPR_of_Chu.m
% PAPR_of_Chu.m
% Plot Fig. 7.10(a)
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
clear, clf
N=16; L=4; i=[0:N-1];
k = 3; X = exp(j*k*pi/N*(i.*i));
[x,time] = IFFT_oversampling(X,N);
PAPRdB = PAPR(x);
[x_os,time_os] = IFFT_oversampling(X,N,L); %x_os=x_os*L;
PAPRdB_os = PAPR(x_os);
subplot(221), plot(x,'o');
hold on, plot(x_os,'k*');
legend('L=1','L=4');
axis([-0.4 0.4 -0.4 0.4]), axis('equal');
plot(0.25*exp(j*pi/180*[0:359])); % circle with radius 0.25
subplot(222), plot(time,abs(x),'o', time_os,abs(x_os),'k:*');
xlabel('时间(由符号间隔归一化)');
ylabel('|IFFT(u1(k))|');
title('IFFT(X1(k)),k=3,N=16,L=1,4');
legend('L=1','L=4');
PAPRdB_without_and_with_oversampling=[PAPRdB PAPRdB_os];
PAPR_of_preamble.m
% PAPR_of_preamble.m
% Plot Fig. 7.10(b) (the PAPR of IEEE802.16e preamble)
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
clear, clf
N=1024; L=4; Npreamble=114; n=0:Npreamble-1; % Mod='BPSK';
%PAPR = zeros(N_preamble,1); PAPR_os = zeros(N_preamble,1);
for i = 1:Npreamble
X=load(['D:\Work\MIMO-OFDM无线通信技术及MATLAB实现\MIMO_OFDM-master\第7章 PAPR\Chu序列和IEEE802.16e前导的PAPR\Wibro-Preamble\Preamble_sym' num2str(i-1) '.dat']);
X = X(:,1); X = sign(X); X = fftshift(X);
x = IFFT_oversampling(X,N); PAPRdB(i) = PAPR(x);
x_os = IFFT_oversampling(X,N,L); PAPRdB_os(i) = PAPR(x_os);
end
plot(n,PAPRdB,'-o', n,PAPRdB_os,':*'),
xlabel('前导编码[0~113]');
ylabel('|IFFT(X1(k))|');
title('IEEE 802.16e前导,L=1,4');
legend('L=1','L=4');
②、仿真结果
1) Chu 序列经 IFFT 之后的幅度
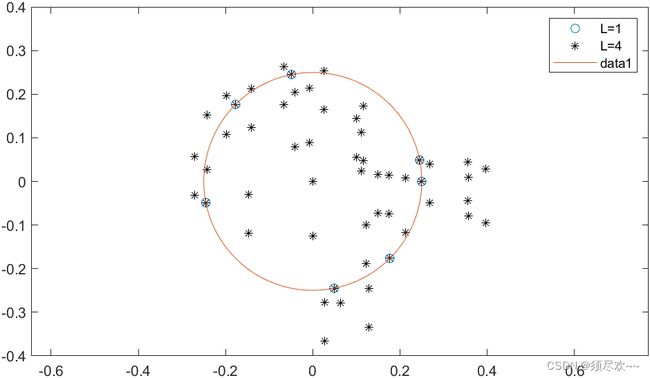

该图显示了在没有采样和 L=4 过采样的情况下,Chu 序列经过 16 点 IFFT 之后的幅度,有过采样和没有过采样的 PAPR 分别为 0dB 和 4.27dB,这说明不同的采样速度会导致 PAPR 具有明显的差异
2) IEEE 802.16e 前导的 PAPR
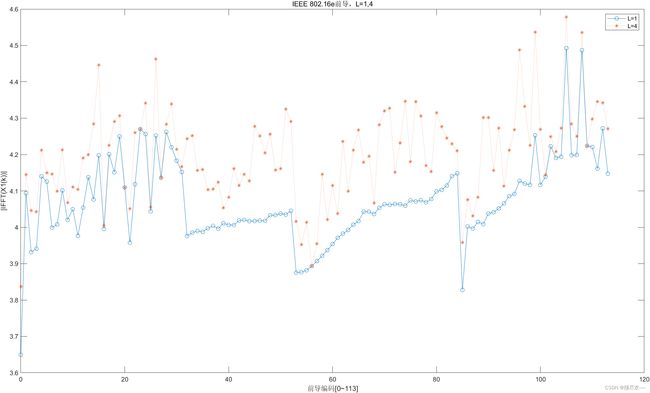
该图显示了 IEEE802.16e 标准中定义的 114 个前导的 PAPR,有过采样的PAPR比没有过采样的 PAPR 大 0.4dB 左右。事实上,由于前导码存在放大功率的问题,因此最初设计的这些前导码具有低的 PAPR。这就是为什么不同的采样速率并没有使这些序列的 PAPR 明显不同。然而,对于 Chu 序列,采样速率的不同通常导致 PAPR 的明显变化。因此,为了在基带对 PAPR 进行精确的测量,需要过采样过程。
5、基于限幅和滤波的 OFDM 信号
①、MATLAB 源码
mapper.m
function [modulated_symbols,Mod] = mapper(b,N)
% If N is given, it generates a block of N random 2^b-PSK/QAM modulated symbols.
% Otherwise, it generates a block of 2^b-PSK/QAM modulated symbols for [0:2^b-1].
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
M=2^b; % Modulation order or Alphabet (Symbol) size
if b==1, Mod='BPSK'; A=1; mod_object=comm.PSKModulator('ModulationOrder', M);
elseif b==2, Mod='QPSK'; A=1;
mod_object = comm.PSKModulator('ModulationOrder', M, 'PhaseOffset', pi/4);
else Mod=[num2str(2^b) 'QAM']; Es=1; A=sqrt(3/2/(M-1)*Es);
mod_object = comm.RectangularQAMModulator('ModulationOrder', M, 'SymbolMapping', 'Gray');
end
if nargin==2 % generates a block of N random 2^b-PSK/QAM modulated symbols
modulated_symbols = A * mod_object(randi([0 M-1], N, 1));
else
modulated_symbols = A * mod_object((0:M-1)');
end
IFFT_oversampling.m
function [xt, time] = IFFT_oversampling(X,N,L)
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
if nargin<3, L=1; end
NL=N*L; T=1/NL; time = [0:T:1-T]; X = X(:).';
xt = L*ifft([X(1:N/2) zeros(1,NL-N) X(N/2+1:end)], NL);
add_CP.m
function y=add_CP(x,Ncp)
% Add cyclic prefix
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
y = [x(:,end-Ncp+1:end) x]; % CP 循环前缀
clipping.m
function [x_clipped,sigma]=clipping(x,CL,sigma)
% CL : Clipping Level
% sigma: sqrt(variance of x)
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
if nargin<3
x_mean=mean(x); x_dev=x-x_mean; sigma=sqrt(x_dev*x_dev'/length(x)); % 计算标准差
end
CL = CL*sigma; % 限幅比 = 输入限幅比 × 标准差
x_clipped = x;
ind = find(abs(x)>CL); % Indices to clip % 找到大于限幅比的索引
x_clipped(ind) = x(ind)./abs(x(ind))*CL; % 进行限幅
PDF_of_clipped_and_filtered_OFDM_signal.m
% PDF_of_clipped_and_filtered_OFDM_signal.m
% Plot Figs. 7.14 and 7.15
%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd
clear
CR = 1.2; % 限幅比
b=2; % 每一QPSK符号的比特数
N=128; % FFT大小
Ncp=32; % CP大小
fs=1e6; % 采样频率
L=8; % 过采样因子
Tsym=1/(fs/N); % 符号周期。它是指每个OFDM符号的持续时间。 Tsym = 1.28e-4
Ts=1/(fs*L); % 采样周期 Ts = 1.25e-7
fc=2e6; wc=2*pi*fc; % 载波频率 wc = 1.2566e+7
t=[0:Ts:2*Tsym-Ts]/Tsym; % 时间向量 t = [0:9.7656e-4:1.999]_{2048}
t0=t((N/2-Ncp)*L); % t0 = t((64-32)*8) = 0.249
f=[0:fs/(N*2):L*fs-fs/(N*2)]-L*fs/2; % -L*fs/2 ~ L*fs/2 的频率向量 [-4e+6, 3.9961e+6]_{2048}
Fs=8; % 滤波器的采样频率 8 MHz
Norder=104; % 滤波器的阶数
dens=20; % 滤波器的密度因子 大于16即可
FF=[0 1.4 1.5 2.5 2.6 Fs/2]; % 阻带/通带/阻带频率边缘向量 [0 Fstop1 Fpass1 Fpass2 Fstop2 Fs/2]
WW=[10 1 10]; % 阻带/通带/阻带加权向量 阻带中的纹波比通带中的纹波小10倍
h = firpm(Norder,FF/(Fs/2),[0 0 1 1 0 0],WW,{dens}); % BPF 系数
X = mapper(b,N); X(1) = 0; % QPSK 调制
x=IFFT_oversampling(X,N,L); % IFFT 和过采样 x = 8*[x(1:64), (0...0)_{1024-128}, x(65:128)]_{1024}
x_b=add_CP(x,Ncp*L); % 加 CP x_b = [(CP)_{256}, x]_{1280}
x_b_os=[zeros(1,(N/2-Ncp)*L), x_b, zeros(1,N*L/2)]; % 多采样 x_b_os = [(0)_{256}, (x_b)_{1280}, (0)_{512}]_{2048}
x_p = sqrt(2)*real(x_b_os.*exp(j*2*wc*t)); % 从基带到通频带
x_p_c = clipping(x_p,CR); % Eq.(7.18) 限幅公式
X_p_c_f= fft(filter(h,1,x_p_c)); % norm(X_p_c_f-X_p_c_f1)
x_p_c_f = ifft(X_p_c_f);
x_b_c_f = sqrt(2)*x_p_c_f.*exp(-j*2*wc*t); % 从通频带到基带
figure(1); clf % Fig. 7.15(a), (b)
nn=(N/2-Ncp)*L+[1:N*L]; nn1=N/2*L+[-Ncp*L+1:0]; nn2=N/2*L+[0:N*L]; % nn =[257:1280]_{1024} nn1 = [257:512]_{256} nn2=[512:1536]_{1025}
subplot(221)
plot(t(nn1)-t0, abs(x_b_os(nn1)),'k:'); hold on; % 循环前缀
plot(t(nn2)-t0, abs(x_b_os(nn2)),'k-'); % 基带信号 + 512个0
axis([t([nn1(1) nn2(end)])-t0 0 max(abs(x_b_os))]);
title(['Baseband signal, with CP']);
xlabel('t (normalized by symbol duration)'); ylabel('abs(x''[m])');
subplot(223)
XdB_p_os = 20*log10(abs(fft(x_b_os)));
plot(f,fftshift(XdB_p_os)-max(XdB_p_os),'k');
xlabel('frequency[Hz]'); ylabel('PSD[dB]'); axis([f([1 end]) -100 0]);
subplot(222)
[pdf_x_p,bin]=hist(x_p(nn),50); bar(bin,pdf_x_p/sum(pdf_x_p),'k');
xlabel('x'); ylabel('pdf'); title(['Unclipped passband signal']);
subplot(224)
XdB_p = 20*log10(abs(fft(x_p)));
plot(f,fftshift(XdB_p)-max(XdB_p),'k');
xlabel('frequency[Hz]'); ylabel('PSD[dB]'); axis([f([1 end]) -100 0]);
figure(2); clf % Fig. 7.15(c), (d)
subplot(221)
[pdf_x_p_c,bin] = hist(x_p_c(nn),50); % 限幅后的通频带信号
bar(bin,pdf_x_p_c/sum(pdf_x_p_c),'k');
title(['Clipped passband signal, CR=' num2str(CR)]);
xlabel('x'); ylabel('pdf');
subplot(223)
XdB_p_c = 20*log10(abs(fft(x_p_c))); % 限幅后的通频带信号功率
plot(f,fftshift(XdB_p_c)-max(XdB_p_c),'k');
xlabel('frequency[Hz]'); ylabel('PSD[dB]'); axis([f([1 end]) -100 0]);
subplot(222)
[pdf_x_p_c_f,bin] = hist(x_p_c_f(nn),50);
bar(bin,pdf_x_p_c_f/sum(pdf_x_p_c_f),'k');
title(['Passband signal after clipping and filtering, CR=' num2str(CR)]);
xlabel('x'); ylabel('pdf');
subplot(224)
XdB_p_c_f = 20*log10(abs(X_p_c_f));
plot(f,fftshift(XdB_p_c_f)-max(XdB_p_c_f),'k'); % 限幅后的基带信号功率
xlabel('frequency[Hz]'); ylabel('PSD[dB]');
axis([f([1 end]) -100 0]);
figure(3); clf % Fig. 7.14
subplot(221)
stem(h,'k'); xlabel('tap'); ylabel('Filter coefficient h[n]'); % 滤波器抽头和系数
axis([1, length(h), min(h), max(h)]);
subplot(222)
HdB = 20*log10(abs(fft(h,length(X_p_c_f)))); % 通频带限幅滤波后经过 FFT 的信号再经过 FFT 后的功率
plot(f,fftshift(HdB),'k');
xlabel('frequency[Hz]'); ylabel('Filter freq response H[dB]');
axis([f([1 end]) -100 0]);
subplot(223)
[pdf_x_p_c_f,bin] = hist(abs(x_b_c_f(nn)),50); % 限幅滤波后基带信号
bar(bin,pdf_x_p_c_f/sum(pdf_x_p_c_f),'k');
title(['Baseband signal after clipping and filtering, CR=' num2str(CR)]);
xlabel('|x|'); ylabel('pdf');
subplot(224)
XdB_b_c_f = 20*log10(abs(fft(x_b_c_f))); % 限幅滤波后基带信号功率
plot(f,fftshift(XdB_b_c_f)-max(XdB_b_c_f),'k');
xlabel('frequency[Hz]'); ylabel('PSD[dB]'); axis([f([1 end]) -100 0]);
②、仿真结果
1)基带信号及通频带信号功率谱、PDF、功率
2)限幅信号、滤波信号的 PDF 和功率谱
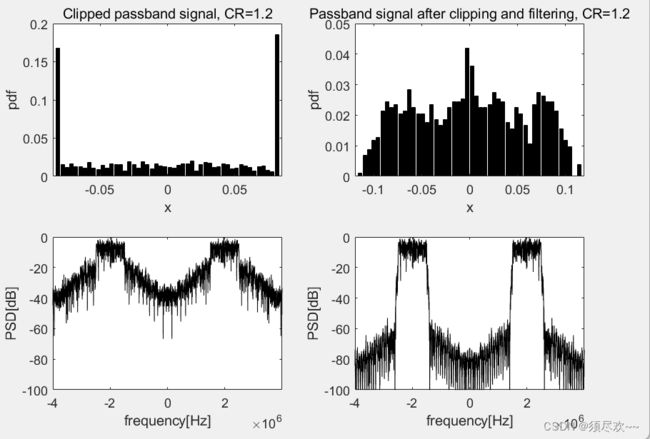
可以看到限幅后的信号幅度低于限幅电平,也可以看到限幅后的带外频谱增大了,但滤波后的带外频谱减小了
3)等波纹通频带 FIR 滤波器的特点
6、采用限幅和滤波后的 PAPR 分布和 BER 性能
因为 CF 是 PAPR 的平方根,所以 CF 的 CCDF 可以看做 PAPR 的分布,从(a)图中可以看出,OFDM 信号的 PAPR 在限幅后显著降低,而在滤波后有所上升。CR 越小,PAPR 降低得越多。(b)图显示了使用限幅和滤波技术的 BER 性能,图中 “C” 表示只有限幅的情况,“C&F” 表示限幅和滤波都有的情况,从(b)可以看出,当 CR 减小时,BER 性能变差。
7、部分传输序列(PTS)
参考我之前的博客:减小PAPR——PTS技术
8、DFT 扩频
参考我之前的博客:减小PAPR——DFT扩频
9、采用脉冲成型的 DFT 扩频的 PAPR 分析
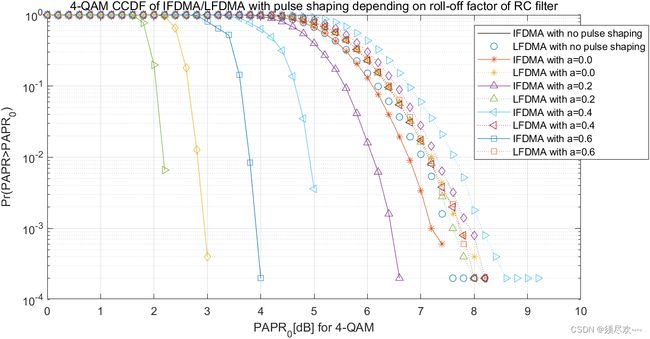
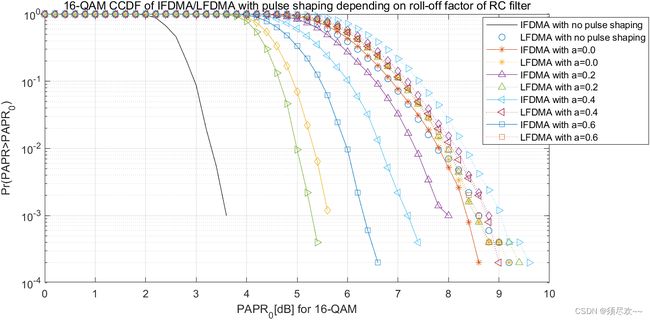
从上面仿真图可以看出,当滚降系数 a 从 0 变到 1 时 IFDMA 的 PAPR 性能显著提升,而 LFDMA 受脉冲成形的影响没有那么大。由于滚降系数增大时剩余带宽增加,IFDMA 可以在剩余带宽和 PAPR 性能之间进行折中
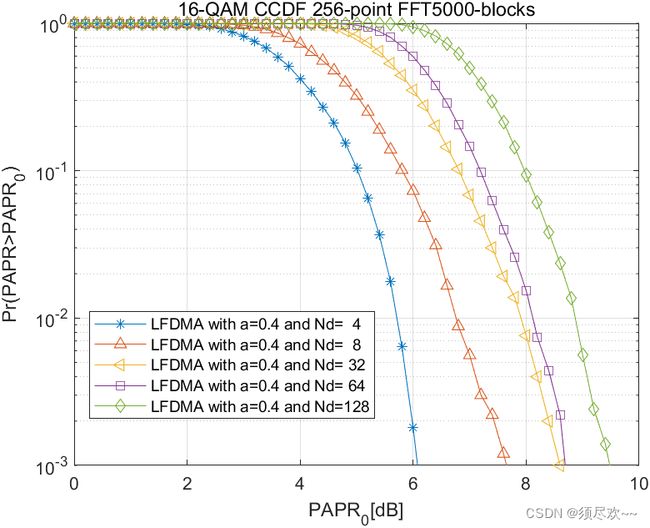
从上面仿真图可以看出,滚降系数 a=0.4 的 LFDMA 中的 DFT 扩频技术的 PAPR 性能随着 M 的增大而降低。
源码下载地址:采用脉冲成型的 DFT 扩频的 PAPR 分析
三、资源自取
OFDM PAPR减小思维导图
我的qq:2442391036,欢迎交流!