python 实现粒子群算法（带绘制)

本文章用python实现了粒子群算法，

标准PSO的算法流程如下：

1. 初始化一群微粒（群体规模为m），包括随机的位置和速度；
2. 评价每个微粒的适应度；
3. 对每个微粒，将它的适应值和它经历过的最好位置pbest的作比较，如果较好，则将其作为当前的最好位置pbest；
4. 对每个微粒，将它的适应值和全局所经历最好位置gbest的作比较，如果较好，则重新设置gbest的索引号；
5. 根据方程变化微粒的速度和位置；
6. 如未达到结束条件（通常为足够好的适应值或达到一个预设最大代数Gmax），回到2）。

 公式为：

# 速度 = 速度 + 学习因子(c1)*rand(0~1)*(最好位置-当前位置)+学习因子(c2)*rand(0~1)*(群体最好位置-当前位置)
# 位置 = 位置+速度

代码如下：

import math
import random
import matplotlib.pyplot as plt
import numpy as np


def initialization(n, v_m, x_1, x_2):  # 初始化粒子群（鸟群）
    p = []
    for i in range(n):
        p.append([random.uniform(-5, 5), random.uniform(-0.5, 0.5), 0, 0, -float('Inf')])  # 位置，速度，当前值，最好位置，最好值
    return p


def fun(x):  # 适应度，这里求最大值
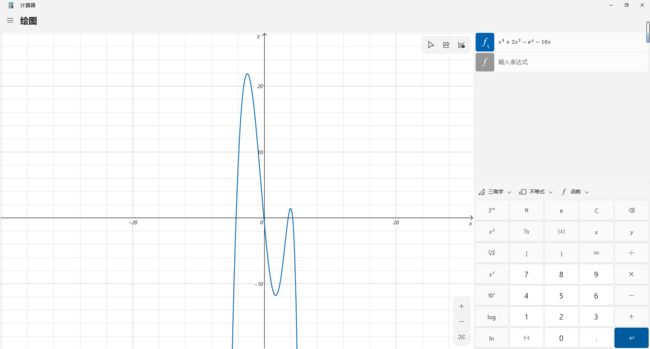
    # ⁅^3+2^2−^−10⁆        可以扔win10计算器里看看长什么样（-5~5）
    return pow(x, 3) + 2 * pow(x, 2) - pow(math.e, x) - 10 * x


def PSO(particle, p_number, v_max, x_max, x_min, loop_max, c1, c2, fig):
    all_good = 0  # 群体最好值的粒子索引
    loop = 0
    while True:
        # 计算所有粒子的值，并更新最好结果
        for i in range(p_number):
            particle[i][2] = fun(particle[i][0])
            if particle[i][2] > particle[i][4]:
                particle[i][3] = particle[i][0]
                particle[i][4] = particle[i][2]
                if particle[i][4] > particle[all_good][4]:  # 超过自己的最优值才能超越群体的最优值
                    all_good = i
        Plt_PSO(fig, particle, x_max, x_min, all_good)  # 绘制图形
        if loop >= loop_max:  # 循环终止条件
            break
        loop += 1
        # 更新速度和位置
        # 速度 = 速度 + 学习因子(c1)*rand(0~1)*(最好位置-当前位置)+学习因子(c2)*rand(0~1)*(群体最好位置-当前位置)
        # 位置 = 位置+速度
        for i in range(p_number):
            particle[i][1] += c1 * random.random() * (particle[i][3] - particle[i][0]) + c2 * random.random() * (
                    particle[all_good][3] - particle[i][0])
            if particle[i][1] > v_max:  # 限制最大速度
                particle[i][1] = v_max
            elif particle[i][1] < -v_max:
                particle[i][1] = -v_max
            particle[i][0] += particle[i][1]
            if particle[i][1] > x_max:  # 限制位置范围
                particle[i][1] = x_max
            elif particle[i][1] < x_min:
                particle[i][1] = x_min
    pass


def Plt_PSO(fig, particle, x_max, x_min, all_good):  # 绘制训练过程
    # 清除上次绘图
    fig.clf()
    # 设置显示范围
    plt.xlim(x_min, x_max)
    scatter_x = [i[0] for i in particle]
    scatter_y = [i[2] for i in particle]
    plt.scatter(scatter_x, scatter_y, c='b', alpha=0.5)  # 绘点散点
    plt.scatter(particle[all_good][3], particle[all_good][4], c='r', alpha=0.8)  # 最好的结果
    plot_x = np.linspace(x_min, x_max, (x_max - x_min) * 20)
    plot_y = [fun(x) for x in plot_x]
    plt.plot(plot_x, plot_y)    # 曲线
    # 刷新图形
    plt.draw()
    plt.pause(0.5)


v_max = 0.25  # 粒子最大速度
x_max = 5  # 最右边界
x_min = -5  # 最左边界
p_number = 10  # 粒子数目
loop_max = 20  # 循环轮数
c1 = 2  # 个体经验系数
c2 = 2  # 群体经验系数
particle = initialization(p_number, v_max, x_max, x_min)
fig = plt.figure()
plt.pause(1)  # 方便录像用，开窗口后等1秒再出图，你们建议删去
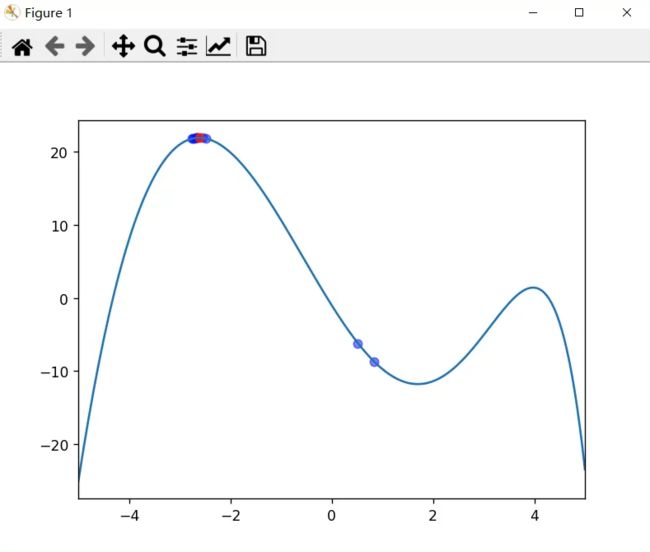
# 结果中，蓝色点就是粒子点，红色的是整个群体到达过的最佳点。
PSO(particle, p_number, v_max, x_max, x_min, loop_max, c1, c2, fig)
plt.show()

所用函数形状为：

这里取-5~5的部分

结果如下：

粒子群算法过程