score-based model介绍

score-based model介绍

参考：https://www.bilibili.com/video/BV1VP411u71p/

论文原文：Generative Modeling by Estimating Gradients of the Data Distribution

引言

宋飏博士的这篇 Generative Modeling by Estimating Gradients of Data Distribution 是第一篇 score-based model 的工作，甚至可以说是近几年第一篇 diffusion 模型的工作。通过预测数据分布的对数梯度（即 score 分数）来构建一个生成模型。score-based model 的核心无疑就是 score，怎么估计 score，求得 score 之后如何进行图片生成，这是理解 score-based model 的两个核心问题。

在当时，主流的生成模型有两个分支，分别是基于似然的模型（likelihood-based model）和隐式的生成模型（implicit generative model）：

• 基于似然的模型
  • 直接建模数据分布
  • 代表方法：VAE、flow-based model
  • 缺点：由于理论推导上的原因，对网络结构有很大的限制（如 VAE 中间隐变量需为高斯分布，flow-based model 网络结构需可逆）
• 隐式的生成模型
  • 间接拟合（如对通过抗训练）数据分布
  • 代表方法：GAN
  • 缺点：训练困难，容易崩

本文提出了一种新的生成模型，即 score-based model。该方法首先通过 score-matching 来估计数据的对数梯度（即 score），然后使用基于退火的朗之万动力学的方法来进行采样，进行数据生成。由于在数据分布比较稀疏的低密度区域，对 score 的估计不是很准，作者提出使用不同强度的高斯噪声对真实数据分布进行扰动，从而提高 score 估计的准确性。在采样时，作者提出了一种退火的朗之万动力学采样方法，加入强度不断递减的噪声扰动，最终逼近真实的数据分布。

score-based model 改善了之前两类方法的缺点。首先，score-based model 对网络结构基本没有限制，任何图到图的网络都可以，其次，score-based model 也不需要对抗训练，优化形式简洁，训练稳定。

方法

score-based model 不是直接学习数据的概率分布 $p_{\theta }(x)$，而是学习 score，即数据分布的对数梯度 ${\nabla }_x\log p_{\theta }(x)$。

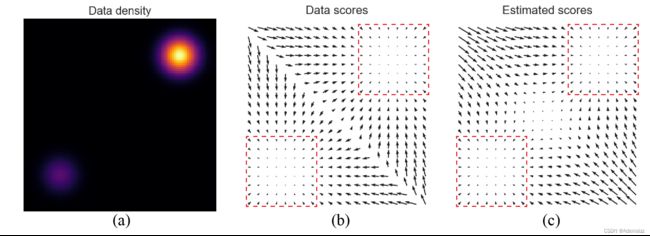
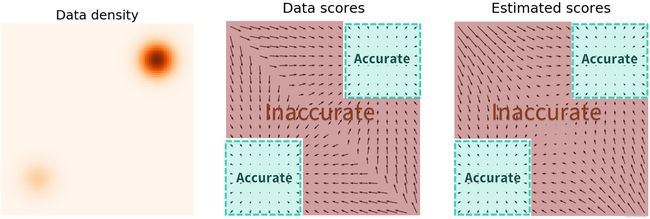
下图分别展示了数据分布的密度，越亮的地方数据密度越高，数据分布的真实 score，和估计的 score，score 是一种梯度，即图中箭头所指的方向。

我们接下来围绕之前提到的 score-based model 中的两个核心问题来进行介绍：如何求 score；求得 score 之后如何采样。我们先看第二个问题。

求得score之后，如何进行采样生成

假设我们已经能够通过某个模型 $s_{\theta }(x)$ 来估计空间中每一个位置的 score（后面会讲究竟如何估计 score），即知道当前位置朝什么方向走能抵达高数据密度区域，那我们就可以按照这个方向走，最终抵达数据分布密集的区域，从而完成采样。具体来说，有如下采样公式：
$$x_{i+1}\leftarrow x_i+ϵ\log p(x)+\sqrt{2ϵ}{z}_i,i=0,1,...,K$$
注意其中 $z_i$ 是一个随机噪声，score-based model 的采样过程是存在随机性的。

看起来很简单，前提是我们已经能够准确地求 score 了。然而问题是，我们并不能准确地估计 score，至少在低数据密度区域，不够准。

在低数据密度区域，模型 $s_{\theta }(x)$ 对于 score 的估计是不准的。而且不幸的是，在整个空间中，高数据密度区域一定是稀疏的。也就是说，刚开始我们随机一个起始位置，几乎必定是落在低数据密度区域的。那么我们采样初期的几步，几乎就是乱走的，而初期乱走，由于高数据密度区域的稀疏性，基本就不可能走到高数据密度区域了，就会一直在低数据密度区域打转。

未加入噪声扰动

为了解决这个问题，使得模型在采样初期，在低数据密度区域，也能够相对较准地估计 score，作者提出对真实数据分布加噪声扰动。在加入噪声扰动之后，数据分布密度较高的位置就会大很多，从而使得模型在前期随机选择的位置，也能够对 score 有较准地估计。极端情况下，如果加的噪声足够大，整个分布几乎成了高斯分布，此时 score 甚至是可以解析的，那么我们当然能准确地求出 score。

加入噪声扰动

然而，加入噪声之后，分布还是我们想要的真实数据分布吗？当然不是，如果加入过强的噪声，最终采样出来的也就是一个噪声了。

这里我们就面临一个两难的问题：如果不加噪声，虽然数据分布是真实的，但对 score 的估计不准，造成我们在低密度数据区域乱转；而如果加入噪声过强，虽然对噪声的估计准了，但最终采样不到我们想要的数据分布。因此，我们需要在准确估计 score 和维持原始分布之间进行权衡。

其实权衡思路也很明确，在采样初期，一定落在低密度区域，score 估计极其不准，这时需要加高强度的噪声扰动，使我们能大致按照正确的方向走，而到了采样的后期，我们已经来到中高密度数据区域，此时就要加较小的噪声扰动，使得我们最终能够采样到真实的数据分布附近。

最终，作者提出了如下退火朗之万动力学的采样算法。在该采样算法中，有两个循环，其中外层循环 i 遍历从 1 到 L，表示不同的噪声级别，级别越高，噪声强度越小；而内层循环 t 从 1 到 T，表示该噪声强度下采样的时间步，总的步数就是 L * T。特别的，如果 T = 1，即在每个噪声强度只采样一步，就类似 DDPM 了。

到这里，我们已经回答了问题 (2)：求得 score 之后如何进行采样生成。即通过在采样不同阶段添加不同程度的噪声扰动，权衡 score 估计的准确性和数据分布的真实性，依据退火的朗之万动力学采样方法，一步一步逼近真实数据的分布。

当然，这一切都是建立在我们已经能够求 score 的前提下，那么 score-based model 究竟是怎么求 score 的呢？

如何求score

求 score 的方法就是之前提到的 score-matching。

这里我们套用 DDPM 的噪声假设，和 score-based model 原文的表示略有出入：
$$x_t\sim \mathcal{N}(\sqrt{{\bar{\alpha }}_t}{x}_0,(1-{\bar{\alpha }}_t)I)$$
该多元高斯分布的分布函数为：
$$p(x_t)\propto \exp \{-\frac{(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0{)}^{\top }(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0)}{2(1-{\bar{\alpha }}_t)}\}$$
我们要求的 score 是：
$${\nabla }_x\log p(x_t)$$
带入得：
$${\nabla }_x\log p(x_t)=-\frac{x_t-\sqrt{{\bar{\alpha }}_t}{x}_0}{1-{\bar{\alpha }}_t}=-\frac{\sqrt{1-{\bar{\alpha }}_t}ϵ}{1-{\bar{\alpha }}_t}$$
可以看到，我们要估计的 score，与噪声 $ϵ$ 实际就差了一个系数。所以说，估计噪声，就相当于估计 score，也就是估计数据分布的对数梯度。DDPM、score-based model 这类扩散模型实际上都是去训练一个去噪网络。

至此，我们就回答了问题 (1)：如何估计 score。答案就是训练一个去噪网络。估计噪声，就是估计 score。

理解这两个问题，就理解了 score-based model 的核心思想。

总结

同为扩散模型。score-based model 在很多地方与 DDPM 非常相近（yang song 后来的文章 也通过 SDE 统一了这两种形式）。通过理解两个关键问题。score-based model 的许多做法似乎有更好的解释性。

如何采样？通过加不同程度的高斯噪声来权衡 score 估计准确性和数据分布真实性。

如何估计 score？估计加入的噪声就是估计 score。