m数据结构 day11 树（五） 霍夫曼树（最优二叉树），霍夫曼编码（压缩编码鼻祖算法）

最基本的压缩编码方法：霍夫曼编码

计算机和网络技术中，文本，图像，音频数据的压缩是非常重要的技术。压缩之后，数据占用的磁盘空间减少，在网络中传输的时间也能减少。但是文本的压缩决不能出错，图像和音频可以进行有损压缩，但是文本必须是无损压缩。

现在已经有很多更新的更好的压缩技术，但这都来源于技术的积累，压缩编码的鼻祖，是霍夫曼编码。

David Huffman,美国数学家，1952年发明了霍夫曼编码。霍夫曼树是他在编码中用到的特殊的二叉树。现在平时用到的压缩和解压技术都是基于霍夫曼68年前的研究发展而来的，实在是伟人一个。

用一个例子引入霍夫曼树：成绩的等级评定

现在很多学校都把学科成绩改为了优秀，良好，中等，及格，不及格这种模糊的评定，而不是直接给出精确的百分制分数。

朴素法，效率感人

但是考试还是要先拿到分数，然后根据分数范围评定成绩等级，下面的代码就可以实现：

这种不断if分支的方式，就是决策树，画出来长这样：

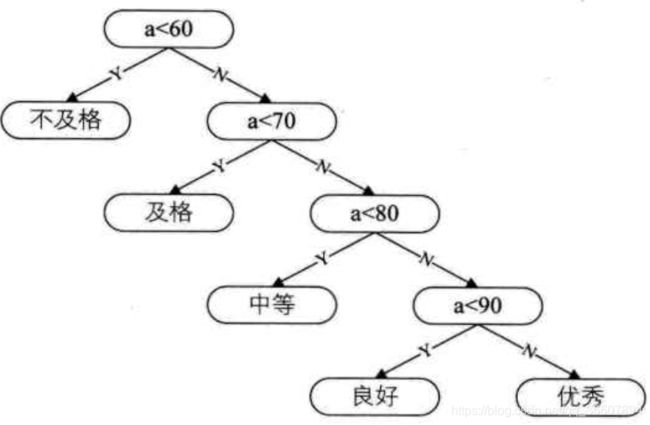
看起来问题是解决了，但是由于问题分析的不够深入，这个办法虽然可行，但是效率很低下。到底是哪里没有想到呢？

考虑一下成绩分布规律，优化效果立竿见影

是没想到成绩的实际分布规律。一般，实际学习中，学生的成绩在这5个等级的分布并不是均等的，而是小部分人是不及格或优秀，大部分人是及格，中等，比如下面的数据：

如果一般都是这种分数分布的话，那么用上面的决策树就可以很快发现导致效率低下的原因：中等占了40%，但是每次需要判断三次才能确定；成绩为良好的概率也有30%，但是需要4次才能判定。而不及格明明只占了5%，却只需要一步就判定了。这样一来，明显平均下来的总判定次数就很多。

怎么解决这个问题呢？学过霍夫曼编码的人可能能想到，霍夫曼编码的思想是，出现概率越大的值的编码越短，出现概率越小的元素的编码越长，这样可以使得最终平均码长最短。我们这里也是一样的道理，出现概率最大的是中等，那么他的判断次数应该最少，出现概率第二的是良好，则良好的判断次数也应该尽量少，而优秀，不及格出现的概率很小，所以需要使用的判定次数多一点也没关系。

基于这样的思想，我们把上面的“朴素决策树”改为：

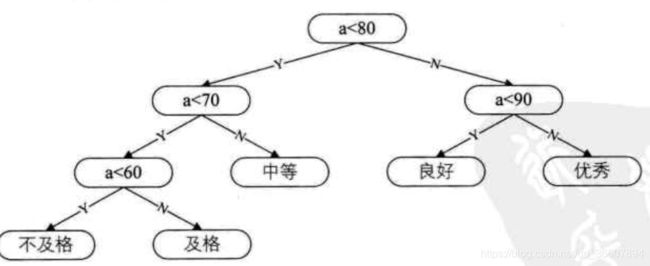
这时候中等和良好需要2次判定，不及格需要三次判定。稍微运用了一点霍夫曼编码思想了，但是还不够，所以这颗树还要继续优化。这时候需要引入更多概念去量化，便于我们找到最优的那颗树，即霍夫曼树。

最优二叉树（霍夫曼树）：带权路径长度WPL最小的二叉树

引入什么概念呢？

需要引入的第一个概念是叶子结点的权值。用ABCDE分别表示不及格，及格，中等，良好，优秀。他们的权值分别是日常比例。

则之前的朴素决策树就可以画为下面这样的二叉树，只有叶子结点带权：

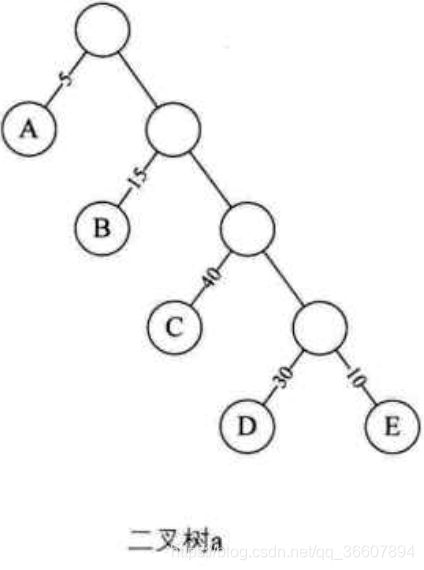
而稍微改进后的决策树的叶子带权后成为：

引入的第二个概念是：路径长度，即从一个结点到另一个结点之间的分支的数目。二叉树a的根结点到A的路径长度是1。

引入的第三个概念是：树的路径长度，即树根到每一个结点的路径长度之和。二叉树a的路径长度是1+1+2+2+3+3+4+4=20，二叉树b的路径长度是1+1+2+2+2+2+3+3= 16。可以看到，经过改进后，二叉树b的路径长度更短了。

引入的第四个概念是：结点的带权路径长度，即树根到该结点之间的路径长度和结点的权的乘积。比如，二叉树a的A结点的带权路径长度是5，B结点的带权路径长度是2*15=30。

引入的第五个概念是：树的带权路径长度WPL，即所有叶子结点的带权路径长度之和。比如，二叉树a的带权路径长度是$5\ast 1+15\ast 2+40\ast 3+30\ast 4+10\ast 4=315$，二叉树b的带权路径长度是$5\ast 3+15\ast 3+40\ast 2+30\ast 2+10\ast 2=220$

可见二叉树b的WPL确实有所改善。改善到什么程度呢？如果有10000个学生的分数需要被评定等级，则二叉树a需要判定31500次，二叉树b只需要判定22000次，少了接近三分之一的判定量，优化地不是一丁点。

带权路径长度WPL最小的二叉树是最优二叉树，被称为霍夫曼树。

如何构造一棵霍夫曼树

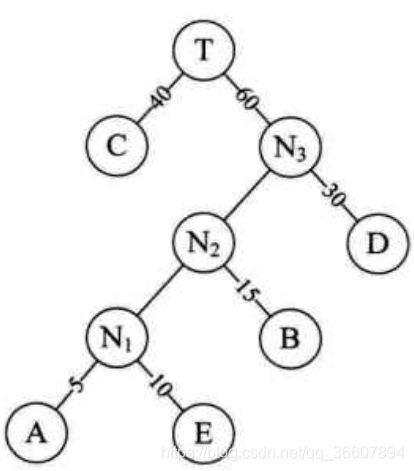
1. 把带权叶子结点们按照权值从小到大的顺序排列。比如上面的成绩等级评定，叶子结点被排序为：A(5),E(10),B(15),D(30),C(40)
2. 取前两个权值最小的结点作为一个新结点N1的两个孩子结点，权值较小者为左孩子。新结点N1的权值为俩孩子结点的权值之和，15。
   
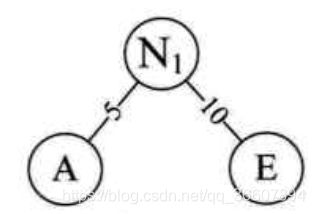
3. 用N1替代A,E，进入有序序列：N1(15),B(15),D(30),C(40)
4. 重复步骤2，即把N1和B作为新结点N2的俩孩子，N2权值为30。
   
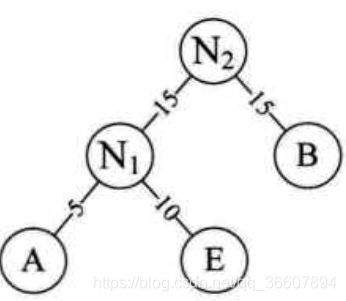
5. N2进入有序序列，N2(30),D(30),C(40),不详述了，直接上图，注意权值小的作为左孩子就好了
   

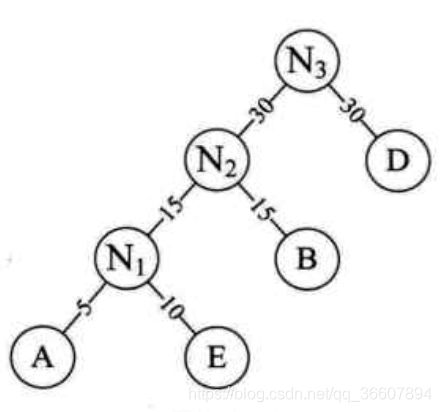
这就是最优的二叉树，即霍夫曼树，我们算一下他的带权路径长度$WPL=40\ast 1+30\ast 2+15\ast 3+10\ast 4+5\ast 4=205$，确实小于刚才的二叉树b哦。

注意如果构造霍夫曼树的过程中，遇到新排列序列中前两个元素不是由相加得到的，就重新开始一颗树。比如：

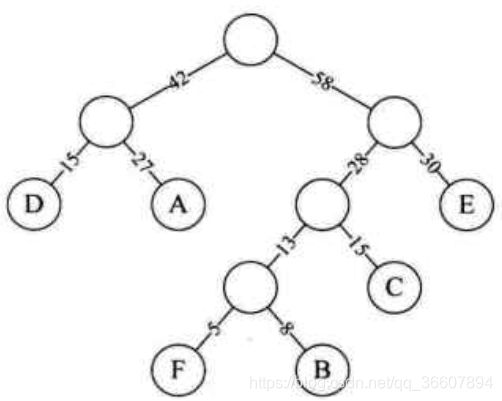
霍夫曼编码：变长编码，前缀编码

霍夫曼研究最优二叉树，是为了解决那个时代的远距离通信（主要是电报）中的数据传输中的最优化问题。

举个例子

一共有6个字母，可以用3位二进制编码表示，即：

如果我们知道了每个字母的出现频率，那么又可以优化了：

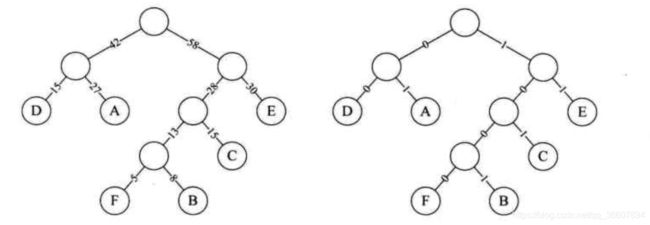
下图左边是构造的霍夫曼树，右图是把权值改为01后的树

于是就得到了每一个字母的霍夫曼编码：

即数据被压缩了，节约了大约六分之一（17%）的存储成本和传输成本。传输字符增多，则这种优势会更大。

接收端怎么解码

一个小前提：霍夫曼编码轻松满足

变长编码必须是前缀编码，即要求每一个字符的编码都不能是另一个字符的编码的前缀！

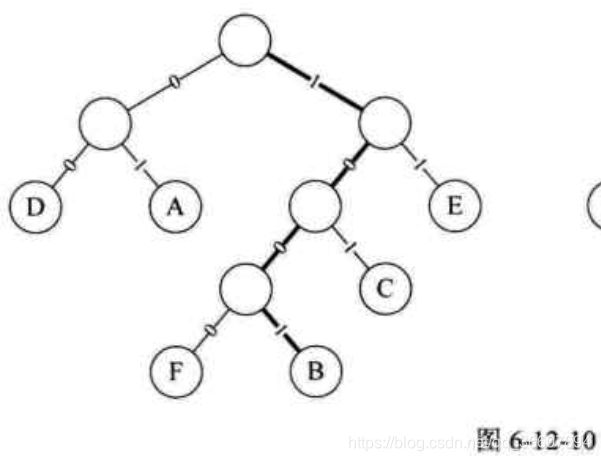
仔细看上面的霍夫曼编码你会发现，霍夫曼编码就是一种前缀编码。F的编码是1000，则不会有结点的编码是1，10，100等。这是因为霍夫曼编码都是叶子结点，前缀编码都是分支结点，不会成为任何字符的编码，从上图的编码树中可以很显然看到。

解码还要用霍夫曼树，发方和收方必须约定好同样的霍夫曼编码规则

总结

霍夫曼树最关键的几个概念是带权叶子结点，结点的路径长度，结点的带权路径长度，树的带权路径长度等。有了这些概念，就可以轻松构建霍夫曼树了，于是就可以要么进行编码，要么进行某种操作，这种最优二叉树都会使得操作次数大大减少，效率大大提高。

示例