FrankMocap

摘要

问题：目前存在的动作捕捉方法要么只聚焦在身体动作捕捉，要么只聚焦在手部动作捕捉。
方法：提出了FrankMocap动作捕捉系统，既可以捕捉身体动作，也可以捕捉手部动作，在速度（9.5 fps）和准确率上都达到SOTA。

介绍

1. 动作捕捉的应用：人机交互，社交人工智能和机器人。
2. 当前存在的问题：
   • 人体姿势估计准确率高但手指姿势被忽略。
   • 手部姿势估计不适合更具挑战性的野外场景。
   • 最近表达手和身体的3D模型相对较慢且不适合实时应用。
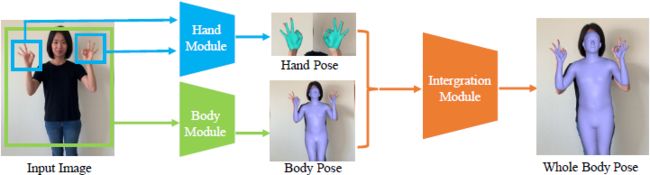
3. 解决方法：提出一个快速准确的运动捕捉方法，单眼RGB.该方法由两个预测身体和手部3D姿势的回归模块和一个集成身体和手部姿势的模块组成。方法的主要思想是使身体姿势模块和手部姿势模块的输出尽可能地兼容，以便更有效地将两者集成一起。身体模块和手部模块基于SMPLX模型贡献了相同输出结构的不同部分，从而实现近实时性能人体3D运动捕捉。

相关工作

3D参数化人体模型

1. SCAPE：解决了形状变化和姿势变化的问题。
2. SMPL：在线性混合蒙皮的顶部学习局部姿势相关的混合形状，以实现整体网格变形和形状变化。
3. MANO：手形变模型。
4. SMPL+H：统一的身体手模型。
5. Adam：身体，手和脸的统一模型。
6. SMPL-X：统一的身体，手和脸模型。

单图像3D人体姿势估计

1. 直接从单个图像中预测3D身体关键点位置-缺少3D关节角度并且不保存身体各部分的长度。
2. 采用参数3D人体模型（SMPL或Adam）-将3D模型拟合到2D观测值，重构3D人体姿势。参数利用深度学习框架直接回归得到。
3. 混合框架-先通过深度学习得到2D和深度的热点图，然后将其拟合到骨骼模型去重建关节角度。
4. 数据集：混合数据集=室内数据集（Human3.6M）+野外数据集（COCO或3DPW）
5. 输入：大多数为单帧图像，少数为序列图像（视频）。

单图像3D手姿势估计

1. 基于深度图像的姿势估计-无法轻松应用于野生RGB图像和视频。
2. 基于单眼RGB的姿势估计-关注3D关节位置而非关节角度。
3. 使用OpenPose预测2D姿势并回归到MANO模型。
4. 使用2D热点图预测模块，同样回归到MANO模型。
5. 预测2D热点图，使用图卷积网络回归手模型顶点。

身体和手的联合3D姿势估计

缺乏用于全身捕捉的数据集-现有方法均采用优化方法，计算时间长。

1. 使用SMPL-X代表整个身体姿势，通过拟合增加约束（身体姿势先验和碰撞惩罚器）的2D关键点优化模型参数。
2. MTC：采用深度神经网络获得2.5D姿势，通过优化获得Adam模型参数。

方法

SMPL-X模型概述

SMPL-X模型可以通过低维形状和姿势参数的组合表示人体的形状变化和于姿势有关的变形。
SMPL-X模型公式：$${\mathbf{V}}_w=W({\varphi }_w,{\theta }_w,{\beta }_w),$$
其中${\varphi }_w\in {\mathbb{R}}^3$为整个人体的整体旋转，${\theta }_w\in {\mathbb{R}}^{(21+15+15)\times 3}$为整个人体姿态相关的变形参数，${\beta }_w\in {\mathbb{R}}^{10}$为人体和手形状的相关参数。将${\theta }_w$分解，${\theta }_w=\{{\theta }_w^b,{\theta }_w^{lh},{\theta }_w^{rh}\}$，其中${\theta }_w^b\in {\mathbb{R}}^{21\times 3}$为身体姿势参数，${\theta }_w^{lh}\in {\mathbb{R}}^{15\times 3}$为左手姿势参数，${\theta }_w^{rh}\in {\mathbb{R}}^{15\times 3}$为右手姿势参数。最后SMPL-X模型输出$V_w\in {\mathbb{R}}^{10475\times 3}$,代表mesh的10475个点。3D关节点位置采用回归函数$R$获得：$${\mathbf{J}}_w^{3D}=R_w({\mathbf{V}}_w)，$$其中${\mathbf{J}}_w^{3D}\in {\mathbb{R}}^{(21+15+15)\times 3}$。
手模型-通过摘取SMPL-X的手部零件定义：$${\mathbf{V}}_h=H({\varphi }_h,{\theta }_h,{\beta }_h),$$其中${\varphi }_h\in {\mathbb{R}}^3$为手的整体旋转，${\theta }_h\in {\mathbb{R}}^{3\times 15}$为手的姿势参数，${\beta }_h$为手的形状参数。最后输入${\mathbf{V}}_h\in {\mathbb{R}}^{778\times 3},$代表手mesh的778个点。通过回归函数得到3D手关节位置：$${\mathbf{J}}_h^{3D}=R_h({\mathbf{V}}_h),$$其中${\mathbf{J}}_h^{3D}\in {\mathbb{R}}^{21\times 3}$。

3D手估计模块

提出单眼3D手姿势估计模块-与最新的单眼身体姿势估计方法相似，用其预测SMPL-X手模型的输入。

手模块结构

该模块是将HMR模型用手姿势估计数据集训练得到的，$M_H$即手模型是端到端的深度神经网络，其定义如下：$$[{\varphi }_h,{\theta }_h,{\beta }_h,c_h]=M_H({\mathbf{I}}_H),$$其中${\mathbf{I}}_H$为裁剪的手部区域RGB图像，$c_h=(t_h,s_h)$为弱透视相机参数，可以将姿势3D手模型投影到输入图像。其中，$t_h\in {\mathbb{R}}^2$用于图像平面上的2D平移，$s_h\in \mathbb{R}$为缩放因子。第$i$个3D手部关节可以被映射如下：$${\mathbf{J}}_{h,i}^{2D}=s_h\Pi ({\mathbf{J}}_{h,i}^{3D})+t_h,$$，其中$\Pi$为正射投影。
手模块结构由一个编码器和一个解码器组成，编码器网络为ResNet-50,从输入图像中获取图像特征，解码器为全连接网络，用来从图像特征中回归手姿势参数。在训练时，使用右手作为训练数据,将左手的图像和标注使用垂直翻转后（相当于右手）进行训练。在测试时，左手先被翻转成右手，然后将输出再翻转回左手空间。

训练方法

三种不同类型标注的损失函数：
$$\begin{gathered} L_{\theta }={\Vert \begin{array}{c}{\theta }_h-{\hat{\theta }}_h\end{array}\Vert }_2^2, \\ {L}_{3D}={\Vert \begin{array}{c}{\mathbf{J}}_h^{3D}-{\hat{\mathbf{J}}}_h^{3D}\end{array}\Vert }_2^2, \\ {L}_{2D}=\Vert \begin{array}{c}{\mathbf{J}}_h^{2D}-{\hat{\mathbf{J}}}_h^{2D}\end{array}\Vert , \end{gathered}$$其中$L_{\theta }$为手姿势参数的损失函数，$L_{3D}$为3D关键点标注的损失函数，$L_{2D}$为2D关键点标注的损失函数。${\hat{\theta }}_h$为真实整体旋转标注，${\hat{\mathbf{J}}}_h^{3D}$为真实3D关键点标注，${\hat{\mathbf{J}}}_h^{2D}$真实2D关键点标注。
手部形状参数的正则项：$$L_{reg}={\Vert \begin{array}{c}{\beta }_h\end{array}\Vert }_2^2，$$用于惩罚不自然的手部形状。
总的损失函数：$$L={\lambda }_1{L}_{\theta }+{\lambda }_2{L}_{3D}+{\lambda }_3{L}_{2D}+{\lambda }_4{L}_{reg}.$$

数据集预处理

3D手势姿势数据集存在的问题：各种数据集的注释类型各不相同。
预处理：1.使用中指的指关节长度作为参考，将所有3D关键点注释缩放到与手模型相兼容。2.重新排序3D关键点，使其与手模型的骨架层次结构相同。

训练数据增强

数据增强策略：随机缩放、随机转换、颜色抖动和随机旋转。
使用模糊核在图像上增加运动模糊以增强模型在野外的表现能力。

3D身体估计模块

通过在训练管道用SMPL-X替换SMPL对SOTA方法进行微调，在训练时，仅使用与SMPL-X模型兼容的姿势参数和2D关键点标注。
身体模块公式：
$$[{\varphi }_b,{\theta }_b,{\beta }_b,c_b]=M_B({\mathbf{I}}_b)，$$其中${\mathbf{I}}_b$是人整个身体的裁剪图像，${\varphi }_b\in {\mathbb{R}}^3$为身体整体旋转，${\theta }_b\in {\mathbb{R}}^{21\times 3}$为身体姿势参数，${\beta }_b\in {\mathbb{R}}^{10}$和${\beta }_w$共享参数。弱透视相机参数$c_b=(t_b,s_b)$和手模型的参数类似。
由于不正确或不充足的标注，存在的身体姿势估计以及本文的身体模块都不能准确的估计手腕和手臂的旋转。

整个身体集成模块

集成模块的作用：将手模块和身体模块的输出集成到SMPL-X模型。

快速的身体和手组成通过复制和粘贴

由于手模块和身体模块输出的手腕格式不同，因此做如下处理：${\theta }_b={\tilde{\theta }}_b\cup \{{\theta }_b^{\mathbf{r}\mathbf{w}\mathbf{r}\mathbf{i}\mathbf{s}\mathbf{t}},{\theta }_b^{\mathbf{l}\mathbf{w}\mathbf{r}\mathbf{i}\mathbf{s}\mathbf{t}}\}$，其中$\tilde{\theta }$为身体模型除手腕之外的姿势参数。整个身体集成表示如下：$$\begin{gathered} {\varphi }_w={\varphi }_b, \\ {\beta }_w={\beta }_b, \\ {c}_w=w_b, \end{gathered}$$$$\begin{gathered} ({\tilde{\theta }}_w^b,{\theta }_w^{lh},{\theta }_w^{rh})=({\tilde{\theta }}_b,{\theta }_{lh},{\theta }_{rh}), \\ ({\theta }_w^{\mathbf{l}\mathbf{w}\mathbf{r}\mathbf{i}\mathbf{s}\mathbf{t}},{\theta }_w^{\mathbf{r}\mathbf{w}\mathbf{r}\mathbf{i}\mathbf{s}\mathbf{t}})=({\Gamma }_l({\theta }_b,{\varphi }_{lh}),{\Gamma }_r({\theta }_b,{\varphi }_{rh})), \end{gathered}$$其中${\Gamma }_l$和${\Gamma }_r$是将手模块获得的整体手腕方向转换为SMPL-X骨架层次结构中父关节局部手腕姿势参数的函数。

手和身体组成通过优化

$$\mathcal{F}([{\varphi }_w,{\theta }_w,{\beta }_w,c_w])={\mathcal{F}}^{2d}+{\mathcal{F}}^{pri},$$其中，${\mathcal{F}}^{2d}$为二维关键点重构三维关键点的代价项，${\mathcal{F}}^{pri}$即先验项，它是三维姿势和形状参数保持在一个可信的空间。

实验

不同模型的速度

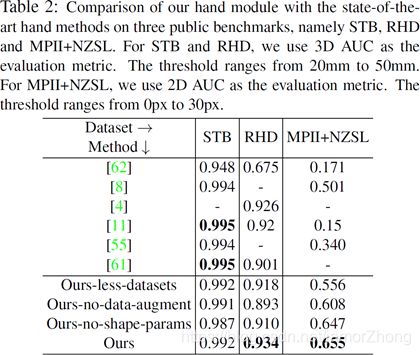
不同手模型的估计精度

数据集消融实验

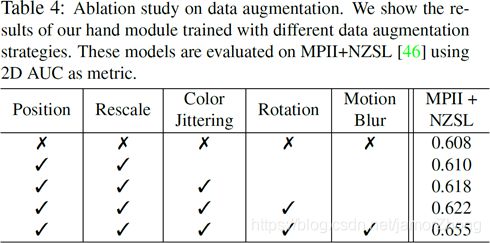
数据增强消融实验

结论

• 设计了一个专业的同时捕捉身体和手的模型
• 提出两种集成策略
• 在手模型上精度达到的了SOTA，且提出的捕捉模型速度快于其他方法。

未来工作

• 双手交互时，手姿势估计效果不佳。
• 在估计人体姿势和手部姿势的时候，人体和手的边界框是需要的。
• 多人交互

附

论文
github