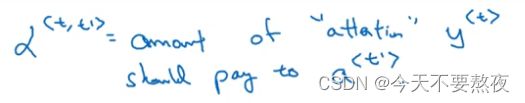一文搞懂Transformers—01（Transformers机制）

Transformer是一种神经网络架构，最初应用在机器翻译领域，但事实证明现在已经可以运用在图像、文本、语音和一些图结构数据，都显示出了这个模型的强大能力。我们通过介绍其机制（01）和变体（02），对Transformer有个大致的了解。（本文参考资料来自邱锡鹏老师和吴恩达老师）

Transformer结构

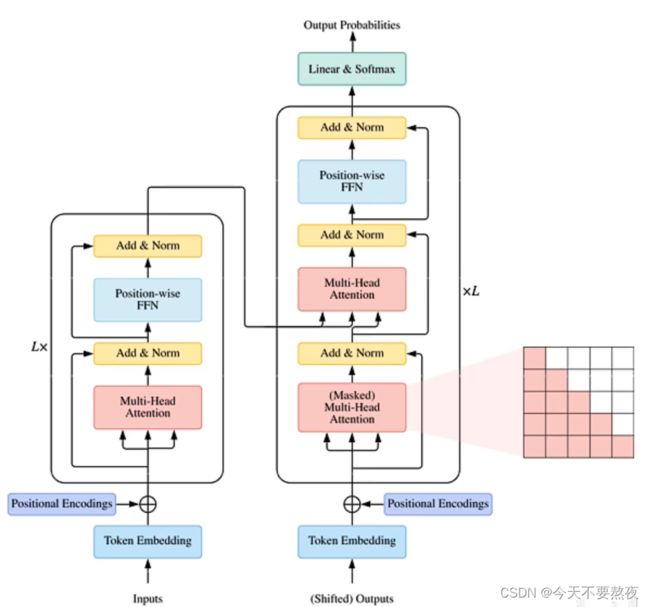
编码器encoder 当输入feed之后，将每一个词映射到一个向量上面（高维到低维称之为嵌入embedding），在此基础上利用Position representation加入位置信息得到含有位置信息的表达，feed到多头自注意力模型，之后利用Layer-Norm、残差、逐位的FFN、Layer-Norm和残差，这样组成Transformer的（一个block），这个block再重复L次（在机器翻译和语言等问题上L一般取12或24，实际上可以任意取）

解码器decoder 实际上在训练中它也是一种特殊的encoder，也是一个上下文编码器，只不过输入呢是shifted outputs（右移的输出），加入位置信息feed到多头自注意力模型（这里注意Self-Attention进行feed的时候是所有词都可以看到的，但是这里我们让他只看到现在及之前位置上的词，屏蔽后面的词，因此需要使用Masked机制）之后利用Layer-Norm、残差，这里我们是机器翻译也需要encoder端的信息，作为K和V，而decoder端作为查询Q，之后就一样了，构成了另外一个block，和编码器一样重复L次

最终通过分类器得到我们要预测的那个值，下面我们依次介绍其中的模块。

Self-Attention（核心模块Module）

我们在下方详细介绍

Position representations

在自注意力模型中所有连接上的权重只和词的内容有关，而与位置无关，但在语言建模中虽然词和词的绝对位置不是很重要，但是相对位置还是需要考虑的，所以在Transformer中运用了位置表示，也很简单，就是将每一个词的绝对位置（1,2,3....）用向量的形式表达出来，和词的嵌入embedding直接加到一起，这样就得到了包含位置信息的词的表示

Layer Normalization

Skip connection（残差连接）

Position-wise FFN（逐位的FFN）

在得到每一个词的上下文表示之后，需要对它进行一个特征变换（通常使用一个两层的MLP来构成，它在所有位置上是共享的，在某种程度上可以认为它是一个窗口为1的卷积）

Attention Model Intuition—和人类一样看一部分翻译一部分

虽然Attention是在机器翻译领域中提出，但现在也已经推广到其他众多领域

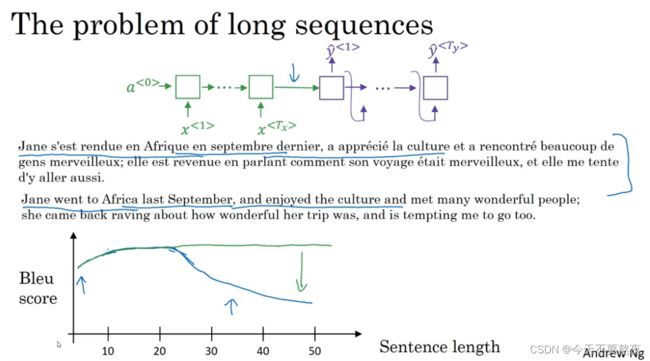
在encoder-decoder结构下，进行机器翻译工作，对于长序列而言需要把整个序列都memorize下来然后再去翻译，而记下很长的序列是我们不想看到的也是效率比较低的，可以看到Bleu score在短序列时较高，当序列越来越长时分数就会降低

而Attention模仿我们人类进行翻译的方式，看一部分翻译一部分，所以不管序列的长度其Bleu score都不会出现明显的下跌（绿色线），这个下跌的程度其实也反映了神经网络记忆一个长序列的能力

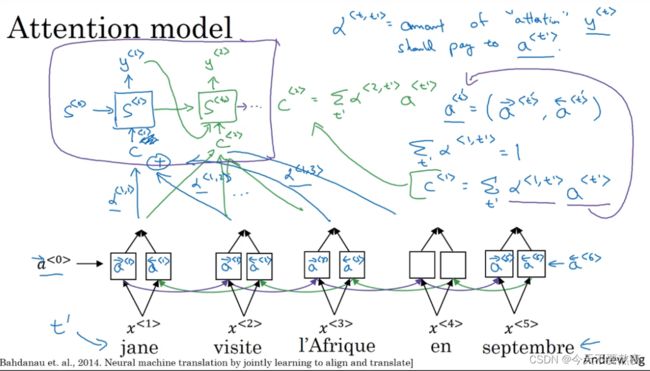
我们先假设有一个输入的法语句子（用t'表示法语句子里面的词）然后利用一个双向的RNN或者双向的GRU或双向的LSTM（LSTM和GRU经常使用在此处）并使用一个RNN，通过下面的双向RNN提供的上下文C去输出英语翻译的每一个词，而这个C来自于注意力参数α，我们定义上下文的方式实际上是将不同时间步的特征相加的方法，这些特征由这些注意力权重加权。

α实际上就是指当我们要翻译出第t个英文词时，需要对t'个法语词pay多少注意力（the amount of attention y should pay to a）

为了简化表示，用a一起来表示t'的前向和后向的特征，于是a就是时间步t'上的特征向量

对于固定一个t值，比如α<1,t'>，要求其加和等于1，这就要利用Softmax，使得其加和等于1

于是接下来就变成了计算e，利用一个小的神经网络，feed s和a，让它自动学习函数

但这个函数有一个缺点就是它要花费quadratic二次方时间（即时间复杂度为O(n^2）），当输入词T_x个，输出词为T_y个，参数总数为T_x * T_y，但是对于机器翻译而言，其输入序列的长度不会太长所以二次方的时间复杂度也是可以接受的。

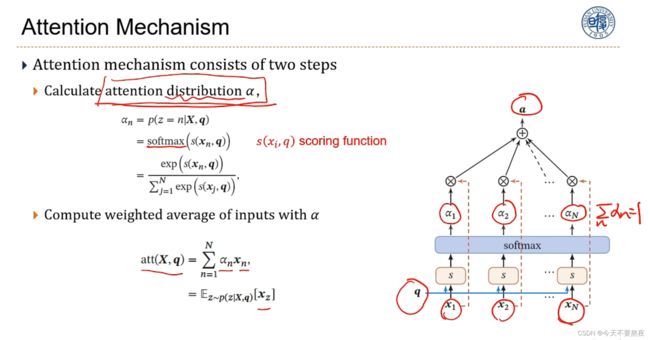
Attention Mechanism

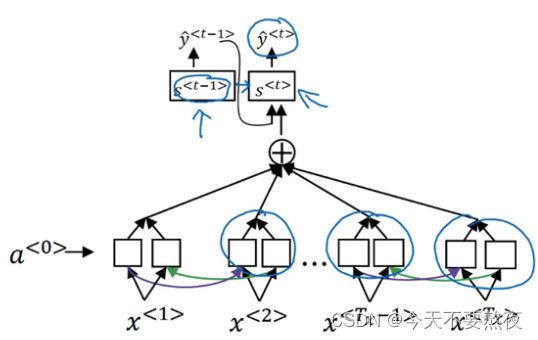
注意力机制包括两步：第一步计算注意力分布（注意力参数），这里的s()函数也就是上面所提到的需要通过小型神经网络学习的，理解它为打分函数，简单一点的可以是做内积或计算相似度，然后利用Softmax归一；第二步就是计算输入x的权重a（也就是上面的c），利用注意力参数和输入x乘积后加和，因为这里的α是注意力分布，相当于计算x的期望

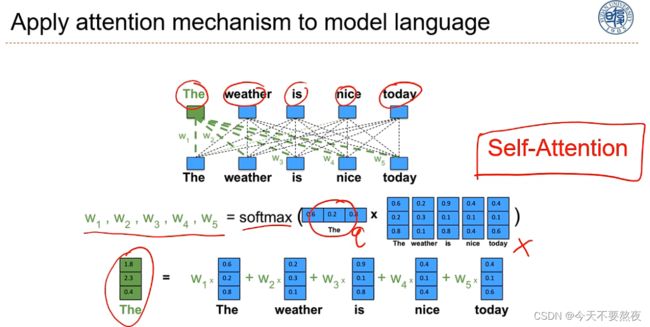
self-attention

当我们计算The的上下文表示，此时就把The作为查询向量q，其他的设为x，通过打分函数s之后过Softmax，再分别加权得到The的上下文表示，同理可以得到其他词的上下文表示，这就完美地解决了全连接中出现的两个问题：1.变长问题，这个机制它和长度没有关系；2.两个词之间的依赖关系要大多数看他的内容而不是位置（因为全连接中，当你改变词的位置时，其对应的关系也会改变）

但这种方式没有外部的查询向量q，查询向量都来自它内部的词，自己attention到自己，所以称之为Self-attention，Self-attention通常是作为大型神经网络的一层，或与其他模型（CNN、RNN等）配合使用，只不过在Transformer中比较独立地使用。

自注意力模型就可以直接建模不同词之间的长程依赖关系，但是在实际使用中显得比较简单，因为他没有可以学习的参数（模型的容量就会很小），一个词既当Query又当候选信息来用

Query-Key-Value（QKV）Model

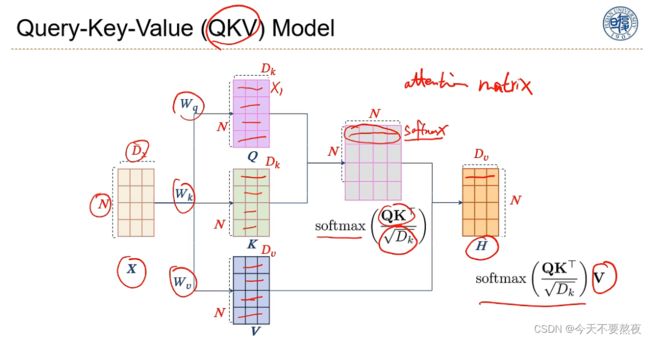
为了提高自注意力模型的能力，我们一般会使用变体—QKV模型：

对于输入X，有N个词，每个词都是Dx维，通过和矩阵Wq、Wk和Wv分别相乘得到Q（每一行就是每一个词，每个词用来表示一个查询）、K、V（K就是索引，V对应了索引K的内容/值），这里的Q和K的维度是一样的（N x Dk）

当Q中的一个词x1要进行查询时，就需要和K里面的（索引）每一行进行内积，就会得到后面这个矩阵的第一行，利用Softmax归一，这也就得到了第一个词对于每一个词的注意力分布了

其实Q乘K转置就会得到注意力矩阵attention matrix，但是由于Softmax的特性：在输入的一组数中当某些数比其他数显著地大时就会使得这个分布变得sharp，所以要对注意力矩阵进行特征缩放，除以一个sqrt（Dk），使得分布更加平滑，然后再过一个Softmax，这样也使得我们的效率提高

因为具有了可以学习的三个参数，Wq、Wk、Wv，所以QKV模型的能力就会变得更强

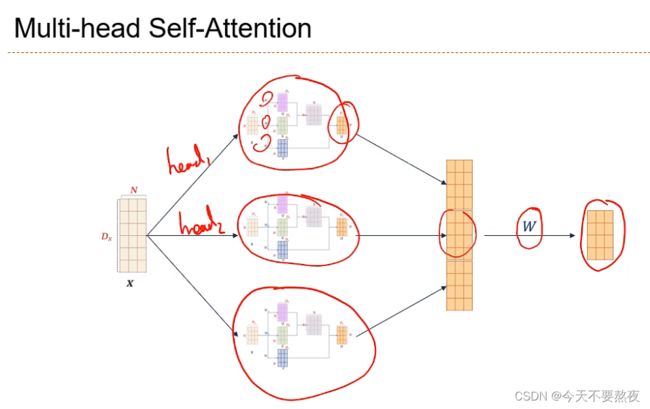
Multi-head Self-Attention

当输入一个X时，通过QKV映射到一个空间，然后在这个空间中计算他们的依赖关系，而这个映射其实可以做多种不同的映射，这里我们做三次不同的映射，在不同的映射中QKV是不同的，每次的映射都是在某种特定的空间中，建立他们的某种特定的语义交互关系，在某种程度上就像我们在卷积中multi-channel的概念（RGB表示的三个channel）得到不同的特征图feature map

在经过不同的映射后把他们组合在一起，然后通过矩阵W映射回到原来的维度

不同的映射称为一个head

Multi-Layer Self-Attention

在多头自注意力机制上，我们可以把它堆叠起来，形成多层的这种注意力结构（以图来看他们的交互关系）在每一个层Layer中每一个点都会收到来自其他所有点的信息，然后再进行下一次的传递

Model Analysis（对模型的复杂度进行分析）

自注意力模型不擅长处理长序列，自然语言处理一般把文档长度限制于512，大于512就视为过于复杂而没法处理

权重矩阵DxD，输入序列长度为T

Self-Attention需要Q（矩阵维度TxD）和K转置乘（DxT），这里有TxT，而后与V（TxD）乘，所以复杂度是TxTxD；Wq、Wk、Wv和最后的W映射回原维度，所以是4

position-wise FNN是对每一个位置上的词进行全连接（维度为DxD）的变化，有T个位置所以复杂度是DxDxT；需要升维再降维，通常是三层，最下层3升维到4，降维回3，所以是（4+4）8

（在经典的应用中是4，事实上不确定，取决于中间这一层升维的这个维度数）