基于遗传算法解决流水车间调度问题

基于简单遗传算法解决流水车间调度问题（FSP）

流水车间调度问题（FSP）

问题描述

n 个工件要在 m 台机器上加工，每个工件需要经过 m 道工序，每道工序要求不同的机器，n 个工件在 m 台机器上的加工顺序相同。工件在机器上的加工时间是给定的，设为
$$t_{ij}(i=\mathrm{1....},n;j=1,...,m)$$

问题的目标

确定 n 个工件在每台机器上的最优加工顺序，使最大流程时间达到最小。

假设（约束条件）

• 每个工件在机器上的加工顺序是给定的
• 每台机器同时只能加工一个工件
• 一个工件不能同时在不同的机器上加工
• 工序不能预定
• 工序的准备时间与顺序无关，且包含在加工时间中
• 工件在每台机器上的加工顺序相同，且是确定的

问题的数学模型

遗传算法原理

基因交换、变异

遗传算法模拟生物学染色体配对过程中基因交换、基因变异对问题进行求解。

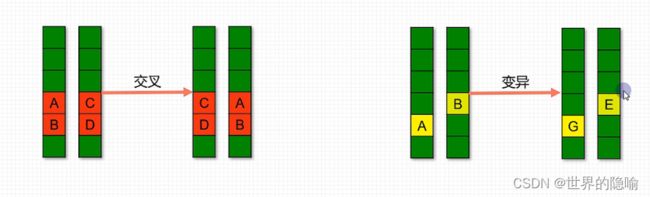
在遗传算法中，可以将问题的一个可行解看成一条染色体，染色体在配对时发生基因交换或者发生基因变异生成新的染色体，即新的可行解。

而新产生的可行解（染色体）参与到下一次基因配对中，产生另一些新的可行解。

比如对于某一个问题的可行解有【1，2，3，4，5】，【2，3，4，5，1】，两个可行解交叉配对之后生成的新可行解可以是【1，3，4，5，5】和【2，2，3，4，1】，然后产生的新可行解在进行配对生成新的可行解。

染色体编码

将问题的可行解抽象化为适用于遗传算法的形式

• 二进制编码，将数值转换为二进制串，用以基因的配对交换、变异
• 旅行商问题，比如 10 个城市，某个解可以表示为【3，2，1，4，5，7，6，8，9，0】
• 根据不同的问题进行不同的抽象实现

适应度

遗传算法模拟生物学染色体配对过程。

以生物学简单理解，适应度可以理解为新生成的染色体的存活能力——一般来说，两个优秀染色体生成的新染色体也是优秀的——所以适应度越高，该染色体留下来（不被淘汰）的概率越大。

以旅行商问题为例，如果问题目标是要求路径最短，那么我们可以认为路径越短的可行解适应度越高，如果要用数值表示适应度，我们可以选择用 1/可行解表示的路径 的方式表示适应度，这样越小的路径表示的适应度数值表示就越大。

染色体配对（复制）

遗传算法的本质是对问题部分的可行解进行交换、变异产生新的可行解，并且希望在这个过程中可以通过较少次数得出该问题的最优解——如果次数过多或者直接产生所有可行解去寻找最优解那么实际上这样的方法和枚举法没有什么区别，反而会浪费时间和资源。

所以遗传算法中选择可行解（染色体）配对交换、变异是很重要的一步，也是算法优化的关键。

遗传算法配对选择的方式多种多样。

• 轮盘赌法——将个体适应度大小映射为概率进行复制：适应度高的个体有更大概率复制，且复制的分数越多。
  1. 将适应度大小映射为概率——比如此时有20个可行解，那么就有20个适应度（比如说 1/路程 ），那么每个可行解映射后的概率为 该可行解的适应度 / 20个可行解的总和
  2. 轮盘赌法的详细介绍（个人理解）—— 比如一开始问题的可行解有20个，即20个染色体，在第一次俩俩配对后生成 N 个可行解，此时问题的可行解有 20+N 个（其中可能有重复的可行解），然后对这 20+N 个可行解的适应度进行降序排序，选择 20+N 个可行解中适应度前 20 的可行解进行下一次染色体配对
• 精英产生精英——对适应度高的前 N/4 的个体纪念性复制，然后用这些个体把后 N/4 个体替换掉
• 不一定要将当前个体的复制体将下一个个体替换掉，可以选择随机选择个体进行配对
• 也不一定把适应度低的个体替换掉——从生物学理解，两个优秀（适应度高）的个体不一定生成的子代一定优秀（适应度高）—— 即遗传算法有很大概率只能找到局部最优解而不是全局最优解
• 还有很多。。。

染色体变异

和染色体配对一样，选择哪个染色体发生变异，或者发生变异的位置选择的策略也是多种多样的

• 每个个体都发生变异
• 只对适应度低的后 N/4 的，或者 N/2 个个体变异
• 按适应度大小映射为概率变异
• 可以选择多个位点进行变异
• 还有很多。。。

适应度映射为概率之后的归一化处理

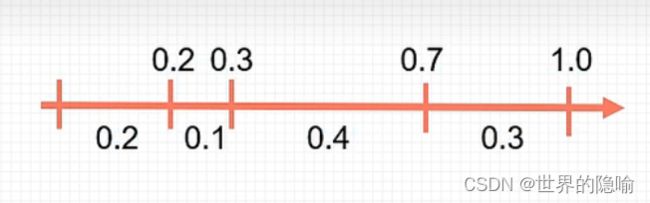
比如此时有 4 个 可行解，根据 适应度 / 适应度的总和 计算映射后的概率，比如此时 4 个可行解适应度映射后的概率为 【0.2，0.1，0.4，0.3】。

面对【0.2，0.1，0.4，0.3】的概率，在选择染色体时我们一般选择 【0.2，0.1，0.4，0.3】长度的 if 判断选择染色体，伪代码如下：

概率 = random.random()
if 概率 < 0.2:
    选择 0.2 对应的染色体
if 0.2 <= 概率 <= 0.2+0.1:
    ...
 ...

理论上这样的代码不报错也是可行的，但实际上这种代码是不合理的，因为假设此时可行解的规模大小是 1万，那么我们就需要写 1万 个 if 条件判断，这显然是不可能的，所以解决办法就是对这些概率进行归一化处理——这样就可以用 循环+if 条件判断解决要写 1万 个 if 判断的麻烦。

伪代码如下：

此时概率列表为 [0.2, 0.3, 0.7, 1.0]
概率 = random.random()
for i in 列表：
	if 概率 < i:
        选择 i 对应的染色体
        break 退出循环
        
'''
解释
如果此时随机的概率为 0.1，那么 0.1<0.2,选择 0.2 所对应的染色体

如果此时随机的概率为 0.5，那么 0.5>0.2, 0.5>0.3, 0.5<0.7, 选择 0.7 所对应的染色体——在判断 0.5和0.7的关系之前，循环已经判断了 0.5 和 0.2，0.3 之间的大小关系，所以在判断0.5 和0.7的关系时，我们已经保证了此时 随机的概率（0.5）不在0.2和0.3的概率范围之内
'''

另一种判断方式的伪代码：

此时概率列表为 [0.2, 0.3, 0.7, 1.0]
概率 = random.random()
概率差值列表 = [概率 - i for i in 概率列表]
for i in 概率差值列表:
    if i < 0: # 选择第一个差值 < 0 的 i 对应的染色体
        选择 i 对应的染色体
        break 退出循环
    continue
 '''
 解释
 随机概率为 0.1
 差值列表为 【-0.1，-0.2，-0.6，-0.9】
 -0.1 是第一个小于0的差值，所以选择 0.2 所对应的染色体
 '''

将流水车间调度问题（FSP）转换成遗传算法模型

染色体编码

每个染色体编码成工件号序列，比如5个工件的一个编码为序列：[5 1 3 4 2]——表示为加工顺序为工件5，工件1，工件3，工件4，工件2

基因交换、变异

在遗传算法中，可以将问题的一个可行解看成一条染色体，染色体在配对时发生基因交换或者发生基因变异生成新的染色体，即新的可行解。

而新产生的可行解（染色体）参与到下一次基因配对中，产生另一些新的可行解。

基因交换

'''
如果交换前的解为
【1 2 3 4 5】 解1
【4 2 5 1 3】 解2

要交换部分为
【2 3 4】
【2 5 1】

交换后解为
【1 2 5 1 5】 解3
【4 2 3 4 3】 解4

我们发现此时两个解加工工件有重复，需要进一步约束
下面就是进一步约束
此时 解1 的 头（head） 为 【1】，被交换过来的部分为 【2 5 1】，交换给解2的部分为 【2 3 4】，其中 1 重复，所以将重复的 解1 的 头（head） 更改为 被交换过来的部分1和交换过去的部分同一位置的数，所以 解3 的头（head） 为 4
解1 的 尾（tail）也一样，改为 3
所以最后的 解3 为 【4 2 5 1 3】
          解4 为 【1 2 3 4 5】
'''

基因突变

# 基因突变，相当于内部相关值进行交换
# 如：原来的解为 【1，2，3，4，5】，基因突变后 【1，3，2，4，5】

适应度

由于问题目标是：确定 n 个工件在每台机器上的最优加工顺序，使最大流程时间达到最小。

所以在该问题中时间越小可行解的适应度就越高，有适应度公式
$$适应度=1/最大流程时间$$

适应度映射为概率之后的归一化处理

适应度映射为概率

$$适应度/适应度的总和=计算映射后的概率$$

归一化处理

选择第二种伪代码

此时概率列表为 [0.2, 0.3, 0.7, 1.0]
概率 = random.random()
概率差值列表 = [概率 - i for i in 概率列表]
for i in 概率差值列表:
    if i < 0: # 选择第一个差值 < 0 的 i 对应的染色体
        选择 i 对应的染色体
        break 退出循环
    continue

具体代码如下

# 适应度概率归一化处理
choice = [choiceList[j] / sum(choiceList) for j in range(len(choiceList))]
# print(choice)
sum_choice = []
for p in range(len(choice)):
	if p == 0:
		sum_choice.append(choice[p])
	else:
		sum_choice.append(choice[p] + sum_choice[p - 1])
		# print(sum_choice)
         # print(rand_num)

'''
选择配对的个体，选择 self.N 个
'''
choice_three = []
for i in range(self.N):
	rand_num = random.random()
	three_change_list = [rand_num - sum_choice[i] for i in range(len(sum_choice))]
	change_index = self.where_change(three_change_list)
	choice_three.append(N_group[change_index])

染色体配对（复制）

遗传算法配对选择的方式多种多样，对该问题我们选择轮盘赌法进行染色体选择。

• 轮盘赌法——将个体适应度大小映射为概率进行复制：适应度高的个体有更大概率复制，且复制的分数越多。
  1. 将适应度大小映射为概率——比如此时有20个可行解，那么就有20个适应度（比如说 1/路程 ），那么每个可行解映射后的概率为 该可行解的适应度 / 20个可行解的总和
  2. 轮盘赌法的详细介绍（个人理解）—— 比如一开始问题的可行解有20个，即20个染色体，在第一次俩俩配对后生成 N 个可行解，此时问题的可行解有 20+N 个（其中可能有重复的可行解），然后对这 20+N 个可行解的适应度进行降序排序，选择 20+N 个可行解中适应度前 20 的可行解进行下一次染色体配对

遗传算法代码

染色体类

# data
# fitness 适应度
class Node:
    def __init__(self,data,fitness):
        self.data = data
        self.fitness = fitness

参数介绍

N = 20  # 群体大小，即进行染色体配对时，染色体规模，配对时只考虑其中 20个 可行解
T = 50  # 终止进化代数
Pc = 0.6 # 交叉概率
Pm=0.1 # 变异概率
n = 5 # 工件个数
machine = 4 # 机器个数

实例化参数

def __init__(self,pc=0.6,pm=0.1,N=5,T=2,n=work_num,machine=machine_num):
    '''
    N = 20  # 群体大小
    T = 50  # 终止进化代数
    Pc = 0.6 # 交叉概率
    Pm=0.1 # 变异概率
    n = 5 # 工件个数
    machine = 4 # 机器个数
    '''

    self.pc = pc
    self.pm = pm
    self.N = N
    self.T = T
    self.n = n
    self.machine = machine

生成初始解

# 生成 N 个（种群规模）的初始解
def init_list(self):
    N_group = []
    for i in range(self.N):
        order_list = [p for p in range(1, self.n + 1)]
        random.shuffle(order_list)
        # node = Node(order_list,fitness(order_list))
        N_group.append(order_list)
    # print(N_group)
    return N_group

计算最大流程时间和适应度

def fitness(self,order_list):
    '''
    根据列表顺序调整整体数据。
    '''
    # 复制 order_list
    three_init_data = copy.deepcopy(order_list)
    # print(three_init_data)

    # 输出
    for j in range(len(order_list)):
        i = order_list[j]
        order_i = str(i)
        three_init_data[j] = source_data[order_i]

    init_data = np.array(three_init_data)
    # print(init_data)

    # k = init_data.shape[0]
    # j = init_data.shape[1] - 1
    # print(k,j)

    def find_time(k, j):
        if k == 1 and j == 1:
            return init_data[0, 1]
        elif k >= 2 and j == 1:
            return find_time(k - 1, 1) + init_data[k - 1, 1]
        elif k == 1 and j >= 2:
            return find_time(1, j - 1) + init_data[0, j]
        else:
            time = max(find_time(k - 1, j), find_time(k, j - 1)) + init_data[k - 1, j]
        return time
    time = find_time(self.n, self.machine)
    # print(time)
    fitness = 1 / time
    print(time)
    return fitness, time

基因交换

def cross_change(self,choice_three):
    changed_list = []
    '''
    函数：两点交叉 传入数据为node列表 长度20
    '''
    def change_main(a1,a2):
        '''
        两点交叉
        传入数据为两个个体
        '''

        a1_copy = copy.deepcopy(a1)
        a2_copy = copy.deepcopy(a2)

        random_1 = random.randint(0, self.n - 1)
        random_2 = random.randint(0, self.n - 1)

        # 确保 random_1 < random_2
        while random_1 > random_2 or random_1 == random_2:
            random_1 = random.randint(0,self.n-1)
            random_2 = random.randint(0,self.n-1)
        # 交换,因为是无脑交换，所以需要考虑交换之后的工件顺序是否有重复，即不能出现交换之后的解为 [1, 4, 3, 1, 5] [4, 2, 2, 3, 5] 的情况
        a1_copy.data[random_1:random_2], a2_copy.data[random_1:random_2] = a2_copy.data[random_1:random_2], a1_copy.data[random_1:random_2]

        intermediate1 = a1.data[random_1:random_2]
        intermediate2 = a2.data[random_1:random_2]

        head1 = []
        head2 = []
        tail1 = []
        tail2 = []

        '''
        如果交换前的解为
        【1 2 3 4 5】 解1
        【4 2 5 1 3】 解2
        要交换部分为
        【2 3 4】
        【2 5 1】
        交换后解为
        【1 2 5 1 5】 解3
        【4 2 3 4 3】 解4
        我们发现此时两个解加工工件有重复，需要进一步约束
        下面子代头尾的代码就是进一步约束
        此时 解1 的 头（head） 为 【1】，被交换过来的部分为 【2 5 1】，交换给解2的部分为 【2 3 4】，其中 1 重复，所以将重复的 解1 的 头（head） 更改为 被交换过来的部分1和交换过去的部分同一位置的数，所以 解3 的头（head） 为 4
        解1 的 尾（tail）也一样，改为 3
        所以最后的 解3 为 【4 2 5 1 3】
                  解4 为 【1 2 3 4 5】
        '''

        # 子代1头
        for i in a1_copy.data[:random_1]:
            while i in intermediate2:
                i = intermediate1[intermediate2.index(i)]
            head1.append(i)