第二十一周:机器学习和深度学习基础回顾
第二十一周:机器学习和深度学习基础回顾
- 摘要
- Abstract
-
- 1. Transformer原理推导
- 2. GAN
- 3. RMSProp 算法
- 总结
摘要
本周复习回顾了Transformer、GAN、RMSProp优化算法,Transformer 模型由 Vaswani 等人在 2017 年提出,引发了自然语言处理领域的一系列重要突破,相比于传统的循环神经网络(RNN)和卷积神经网络(CNN),Transformer 模型使用了自注意力机制(self-attention mechanism),能够更好地捕捉文本中的长距离依赖关系。Transformer 模型的基本组成部分是多层的自注意力层和前馈神经网络。GAN 由两个神经网络组成:生成器网络(Generator Network)和判别器网络(Discriminator Network)。生成器网络通过学习从一个随机噪声向量生成类似于训练数据的样本。判别器网络则被训练成能够区分生成器生成的样本和真实的训练数据样本。两个网络通过对抗性的训练过程进行迭代学习。本文将详细介绍Transformer、GAN、RMSProp原理细节。
Abstract
This week’s review reviewed the optimization algorithms of Transformer, GAN, and RMSProp. The Transformer model was proposed by Vaswani et al. in 2017, which triggered a series of important breakthroughs in the field of natural language processing. Compared to traditional recurrent neural networks (RNNs) and convolutional neural networks (CNNs), the Transformer model uses a self attention mechanism, which can better capture long-distance dependencies in text. The basic components of the Transformer model are multi-layer self attention layers and feedforward neural networks. GAN consists of two neural networks: the Generator Network and the Discriminator Network. The generator network learns to generate samples similar to training data from a random noise vector. The discriminator network is trained to distinguish between the samples generated by the generator and the real training data samples. Two networks iteratively learn through adversarial training processes. This article will provide a detailed introduction to the principles and details of Transformer, GAN, and RMSProp.
1. Transformer原理推导
RNN模型是分阶段执行的,即第一个时间段执行完后,才开始执行下一个时间点,整体执行过程为串行,输入序列需要一个个输入进模型中,输出序列也是一个个输出,这样的效率和性能较低。而Transformer拥有其强大的完全自注意力机制,能够实现序列处理的并行化,即输入一排向量,输出一排向量。
下面,我们来具体看一下Attention机制的推导过程以及每个词的注意力分数是如何计算的:
我们首先输入四个词向量 x 1 、 x 2 、 x 3 、 x 4 x^1、x^2、x^3、x^4 x1、x2、x3、x4,它们各自会分别乘上 W q 、 W k 、 W v W_q、W_k、W_v Wq、Wk、Wv,生成新向量 q ( q u e r y ) 、 k ( k e y ) 、 v ( v a l u e ) q(query)、k(key)、v(value) q(query)、k(key)、v(value),这里的 W q 、 W k 、 W v W_q、W_k、W_v Wq、Wk、Wv为四个词向量共享的参数,计算公式如下 q i = W q x i q^{i}=W_{q}x^{i} qi=Wqxi k i = W k x i k^{i}=W_{k}x^{i} ki=Wkxi v i = W v x i v^{i}=W_{v}x^{i} vi=Wvxi我们以输出第一个向量 y 1 y^{1} y1为例,来了解一下attention机制的全部流程:
- 首先向量 q 1 q^{1} q1会和每个词向量对应的的 k k k 向量作内积,在本例中, q 1 q^{1} q1 和 k 1 k^{1} k1 内积得到 α 1 , 1 \alpha_{1,1} α1,1, q 1 q^{1} q1 和 k 2 k^{2} k2 内积得到 α 1 , 2 \alpha_{1,2} α1,2, q 1 q^{1} q1 和 k 3 k^{3} k3 内积得到 α 1 , 3 \alpha_{1,3} α1,3, q 1 q^{1} q1 和 k 4 k^{4} k4 内积得到 α 1 , 4 \alpha_{1,4} α1,4,在这里, α \alpha α代表的是每个词的注意力分数,该值越大,就说明这个位置更重要一些。
- 然后所有的 α \alpha α 注意力分数会通过一个softmax层,得到 α ′ \alpha^{'} α′,分别为 α 1 i ′ , i = 1 , 2 , 3 , 4 \alpha^{'}_{1i},i=1,2,3,4 α1i′,i=1,2,3,4,如下图所示:

- 然后我们将得到的 α ′ \alpha^{'} α′与其对应词向量的 v v v 相乘,让 α 1 , 1 ′ \alpha^{'}_{1,1} α1,1′乘上 v 1 v^{1} v1、 α 1 , 2 ′ \alpha^{'}_{1,2} α1,2′乘上 v 2 v^{2} v2、 α 1 , 3 ′ \alpha^{'}_{1,3} α1,3′乘上 v 3 v^{3} v3、 α 1 , 4 ′ \alpha^{'}_{1,4} α1,4′乘上 v 4 v^{4} v4,将所有的乘积结果相加起来,得到最终的输出 y 1 y^{1} y1,如下图所示:

我们可以发现 α ′ \alpha^{'} α′ 相当于是向量 v v v 的权重,假设 α 1 , 2 ′ \alpha^{'}_{1,2} α1,2′的值很大,那么我们在做按权求和的时候, v 2 v^{2} v2就会有更多的信息传入到 y 1 y^{1} y1,即 v 2 v^{2} v2得到了更多的关注。
下面我们用矩阵变换的思维回顾下这一整个过程:
首先是 x x x 向量分别乘上 W q 、 W k 、 W v W_q、W_k、W_v Wq、Wk、Wv,生成 q 、 k 、 v q、k、v q、k、v 向量,这里,我们以生成 q 2 q_2 q2 向量为例,假设目标 q 2 q_2 q2的维度为2,输入向量 x 2 x_2 x2的维度为3,那么我们就需要训练一个2*3的矩阵进行转换,这里的 W q W_q Wq 为两行三列, x 2 x^2 x2为三行一列,这里实现了 x 2 x^2 x2 到 q 2 q^2 q2 的转换,同理,可以依次得到 q 1 、 q 3 、 q 4 q^1、q^3、q^4 q1、q3、q4,然后我们将向量拼接成一个矩阵,同理,按照这种方式,可以得到 K 、 V K、V K、V矩阵
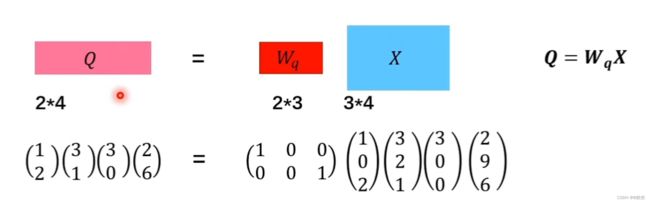
接下来分别让 q 2 q^2 q2与 k 1 、 k 2 、 k 3 、 k 4 k^1、k^{2}、k^3、k^4 k1、k2、k3、k4做内积,分别得到 α 2 , 1 、 α 2 , 2 、 α 2 , 3 、 α 2 , 4 \alpha_{2,1}、\alpha_{2,2}、\alpha_{2,3}、\alpha_{2,4} α2,1、α2,2、α2,3、α2,4,这里得到的 α 2 , 1 、 α 2 , 2 、 α 2 , 3 、 α 2 , 4 \alpha_{2,1}、\alpha_{2,2}、\alpha_{2,3}、\alpha_{2,4} α2,1、α2,2、α2,3、α2,4均是 1 * 1 的向量,由于 q 2 q^2 q2为 2 * 1 的向量, k 1 k^1 k1 为 2 * 1 的向量,此时我们需要将 k k k 进行转置,将其转换成 1 * 2 的向量,最终得到的 α 2 , i \alpha_{2,i} α2,i 均为 1 * 1 的向量,我们可以将这四次矩阵运算整合成一次,将转置后的每个词向量的 k k k 上下堆叠,因此最终得到一个 4 * 1 的 α \alpha α 向量。

同理可以计算出其他词向量的注意力得分,将 α \alpha α 矩阵记为 A A A,将堆叠的 k k k 记为 K T K^{T} KT,将 q q q 记为 Q Q Q, A = K T Q A=K^{T}Q A=KTQ
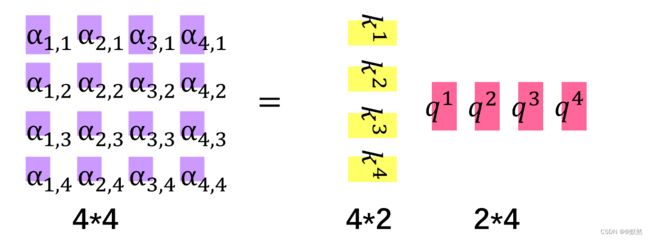
然后将每一列的 α \alpha α 做一次 softmax 的操作,进行归一化,即 A ′ = s o f t m a x ( A ) A^{'}=softmax(A) A′=softmax(A)

最终我们将所有的 α 2 , i \alpha_{2,i} α2,i乘上 v i v^i vi,然后将其相加,得到 y 2 = α 2 , 1 v 1 + α 2 , 2 v 2 + α 2 , 3 v 3 + α 2 , 4 v 4 y^{2}=\alpha_{2,1}v^{1}+\alpha_{2,2}v^{2}+\alpha_{2,3}v^{3}+\alpha_{2,4}v^{4} y2=α2,1v1+α2,2v2+α2,3v3+α2,4v4,按照此思路,我们可以计算出其他词向量的输出值。
从上述推导过程中,我们可以发现,attention机制是忽视序列长度的,无论两个输入向量相隔有多远,q与k做内积,就能知道当前的词需要放多少注意力在序列中的各个词上,做到了通过语境、语意同步,联系了上下文。在处理序列任务的attention模型中,常常会对输入的词向量进行位置编码,对不同位置的词向量,加上不同的位置向量
2. GAN
通俗来说,GAN要做的事情就是根据很多example去进行生成,所谓生成,到底是一个什么样的问题呢?
假设我们现在要生成的是一个图像,我们用x来代表这个图像,即x是一个高维空间的一个向量。在这个例子中,为了画图方便,我们假设每一个x是二维空间上的一个点。我们现在要生成的图像,它其实是有一个固定的distribution,在这里,我们将它写成 P d a t a ( x ) P_{data}(x) Pdata(x),在整个图像所构成的高维空间中,其实只有非常少的部分,它sample出来的图像看起来像是目标图像,在多数的空间中sample出来的图像都不像是目标图像,如下图,可能只有下图中蓝色区域去sample出来的图像才像是目标图像,而我们需要让机器找出这种distribution,而具体这种distribution是什么样子,我们是不知道的。
在有GAN之前,我们通过Maximum Likelihood Estimation(最大似然估计)来找这种distribution。具体步骤如下:
- 首先我们有一个 P d a t a ( x ) P_{data}(x) Pdata(x)的distribution,这个distribution具体是什么,我们是不知道的。我们需要从这个distribution种sample出一些data出来。
- 我们要找一个distribution,这个distribution由 P G ( x ; θ ) P_{G}(x;\theta) PG(x;θ)表示,而 θ \theta θ 是决定这个distribution的参数,我们的目的是为了通过调整 θ \theta θ ,使得 P G ( x ; θ ) P_{G}(x;\theta) PG(x;θ) 和 P d a t a ( x ) P_{data}(x) Pdata(x)越接近越好。这个过程需要我们先从 P d a t a ( x ) P_{data}(x) Pdata(x)种sample出 { x 1 , x 2 , x 3 , . . . , x m {x^1,x^2,x^3,...,x^m} x1,x2,x3,...,xm},而这些sample出来的 x i x^i xi,我们都可以计算它的Likelihood(几率),即假设给定一组 θ \theta θ,我们就知道 P G ( x i ; θ ) P_{G}(x^i;\theta) PG(xi;θ) 的概率分布是什么样子,然后我们就可以计算从这个概率分布里sample出某一个 x i x^i xi 的几率,从而计算出 Likelihood,而接下来要做的就是,我们要找出一组 θ \theta θ,使得 P G ( x ; θ ) P_{G}(x;\theta) PG(x;θ) 和 P d a t a ( x ) P_{data}(x) Pdata(x)越接近越好,即我们需要从 P d a t a ( x ) P_{data}(x) Pdata(x)种sample出 { x 1 , x 2 , x 3 , . . . , x m {x^1,x^2,x^3,...,x^m} x1,x2,x3,...,xm},如果用 P G ( x ; θ ) P_{G}(x;\theta) PG(x;θ)来产生的话,它的Likelihood越大越好。那每个data从 P G ( x ; θ ) P_{G}(x;\theta) PG(x;θ)里产生的Likelihood,我们都是可以计算出来的,我们把所有的Likelihood相乘,得到一个总的Likelihood,在这里我们用 L 来表示,即这个总的Likelihood越大越好,如下公式: L = ∏ i = 1 m P G ( x i ; θ ) L=\prod_{i=1}^{m}P_{G}(x^i;\theta) L=i=1∏mPG(xi;θ)我们需要找一组最佳的参数 θ ∗ \theta^* θ∗ 使得 L 最大化。公式推导如下:

我们寻找一个 θ ∗ \theta^* θ∗ 来最大化这个似然,等价于最大化log似然。因为此时这m个数据是从真实分布中取得,所以也就约等于真实分布中的所有x在 P G P_G PG 分布中的log似然的期望。真实分布中的所有x的期望,等价于求概率积分,可以转化为积分运算,因为减号后面的项和 θ \theta θ 无关,所以添加上之后还是等价的。然后提出共有的项,括号内的反转,max变为min,就可以转化为KL散度的形式了,KL散度描述的是2个向量之间的差异。所以最大化似然,让generator最大概率的生成真实图片,也就是要找一个 θ \theta θ 让 P G P_G PG 更接近于 P d a t a P_{data} Pdata,那如何来找这个最合理的 θ \theta θ 呢?
我们可以假设 P G ( x , θ ) P_G(x,\theta) PG(x,θ)是一个神经网络。首先随机一个向量z,通过G(z)=x这个网络生成图片x,那么如何比较两个分布是否相似呢?z是从高斯分布中sample出来的,那么通过网络就可以生成一个非常复杂的分布,那么这个分布就是所谓的 P G P_G PG,然后来和真实分布 P d a t a P_{data} Pdata比较。下图便是上述的过程。

则有 G ∗ = a r g m i n G D i v ( P G , P d a t a ) G^{*}=argmin_{G}Div(P_{G},P_{data}) G∗=argminGDiv(PG,Pdata)我们要找一个generator G,这个generator G可以让它所定义出来的 P G P_G PG和 P d a t a P_{data} Pdata之间的某种divergence越小越好。那么我们该如何计算这个divergence呢?具体计算过程请参考 第八周:深度学习基础 中的GAN理论部分,这里不过多赘述。根据上周所学习的GAN理论中,我们知道GAN的公式为: V ( G , D ) = E y ∼ P d a t a [ l o g D ( y ) ] + E y ∼ P G [ l o g ( 1 − D ( y ) ) ] V(G,D)=E_{y \sim P_{data}}[logD(y)]+E_{y \sim P_{G}}[log(1-D(y))] V(G,D)=Ey∼Pdata[logD(y)]+Ey∼PG[log(1−D(y))]这个式子的好处在于,固定G,max V(G, D)就表示 P G P_G PG和 P d a t a P_{data} Pdata之间的差异,然后要找一个最好的G,让这个最大值最小,也就是2个分布之间的差异最小。 G ∗ = a r g m i n G m a x D V ( G , D ) G^* = argmin_{G}max_{D}V(G,D) G∗=argminGmaxDV(G,D)表面上看这个的意思是,D要让这个式子尽可能的大,也就是对于x是真实分布中,D(x)要接近与1,对于x来自于生成的分布,D(x)要接近于0,然后G要让式子尽可能的小,让来自于生成分布中的x,D(x)尽可能的接近1。现在我们先固定G,来求解最优的D:
我们现在是目的是为了找一个 D ∗ D^{*} D∗,使得 P d a t a ( x ) l o g D ( x ) + P G ( x ) l o g ( 1 − D ( x ) ) P_data(x)logD(x)+P_{G}(x)log(1-D(x)) Pdata(x)logD(x)+PG(x)log(1−D(x))这个式子最大,在这里,我们用 a a a 表示 P d a t a P_{data} Pdata,用 D D D 表示 D ( x ) D(x) D(x),用 b b b 表示 P G P_{G} PG,因此整个式子可以改写为: f ( D ) = a l o g ( D ) + b l o g ( 1 − D ) f(D)=alog(D)+blog(1-D) f(D)=alog(D)+blog(1−D),接下来便是求 f ( D ) f(D) f(D) 对 D D D 的微分,如上图的计算过程,求出 D ∗ ( x ) D^{*}(x) D∗(x),将 D ∗ ( x ) D^{*}(x) D∗(x)代入 V ( G , D ) = E x ∼ P d a t a [ l o g D ( x ) ] + E x ∼ P G [ l o g ( 1 − D ( x ) ) ] V(G,D)=E_{x \sim P_{data}}[logD(x)]+E_{x \sim P_{G}}[log(1-D(x))] V(G,D)=Ex∼Pdata[logD(x)]+Ex∼PG[log(1−D(x))]中得到: V = E x ∼ P d a t a [ l o g D ∗ ( x ) ] + E x ∼ P G [ l o g ( 1 − D ∗ ( x ) ) ] V=E_{x \sim P_{data}}[logD^{*}(x)]+E_{x \sim P_{G}}[log(1-D^{*}(x))] V=Ex∼Pdata[logD∗(x)]+Ex∼PG[log(1−D∗(x))]即 V = E x ∼ P d a t a [ l o g P d a t a ( x ) P d a t a ( x ) + P G ( x ) ] + E x ∼ P G [ l o g ( 1 − P d a t a ( x ) P d a t a ( x ) + P G ( x ) ) ] V=E_{x \sim P_{data}}[log\frac{P_{data}(x)}{P_{data}(x)+P_G(x)} ]+E_{x \sim P_{G}}[log(1-\frac{P_{data}(x)}{P_{data}(x)+P_G(x)} )] V=Ex∼Pdata[logPdata(x)+PG(x)Pdata(x)]+Ex∼PG[log(1−Pdata(x)+PG(x)Pdata(x))] = ∫ x P d a t a [ l o g P d a t a ( x ) ∗ 1 2 ( P d a t a ( x ) + P G ( x ) ) 1 2 ] d x + ∫ x P G [ l o g P d a t a ( x ) ∗ 1 2 ( P d a t a ( x ) + P G ( x ) ) 1 2 ] d x =\int_{x}^{}P_{data}[log\frac{P_{data}(x)*\frac{1}{2} }{(P_{data}(x)+P_G(x))\frac{1}{2} } ]dx+\int_{x}^{}P_{G}[log\frac{P_{data}(x)*\frac{1}{2} }{(P_{data}(x)+P_G(x))\frac{1}{2} } ]dx =∫xPdata[log(Pdata(x)+PG(x))21Pdata(x)∗21]dx+∫xPG[log(Pdata(x)+PG(x))21Pdata(x)∗21]dx = − 2 l o g 2 + ∫ x P d a t a [ l o g P d a t a ( x ) ( P d a t a ( x ) + P G ( x ) ) 1 2 ] d x + ∫ x P G [ l o g P d a t a ( x ) ( P d a t a ( x ) + P G ( x ) ) 1 2 ] d x =-2log2+\int_{x}^{}P_{data}[log\frac{P_{data}(x) }{(P_{data}(x)+P_G(x))\frac{1}{2} } ]dx+\int_{x}^{}P_{G}[log\frac{P_{data}(x) }{(P_{data}(x)+P_G(x))\frac{1}{2} } ]dx =−2log2+∫xPdata[log(Pdata(x)+PG(x))21Pdata(x)]dx+∫xPG[log(Pdata(x)+PG(x))21Pdata(x)]dx = − 2 l o g 2 + K L ( P d a t a ∣ ∣ P d a t a + P G 2 ) =-2log2+KL(P_{data}||\frac{P_{data}+P_{G}}{2} ) =−2log2+KL(Pdata∣∣2Pdata+PG) = − 2 l o g 2 + 2 J S D ( P d a t a ∣ ∣ P G ) =-2log2+2JSD(P_{data}||P_G) =−2log2+2JSD(Pdata∣∣PG)因此最大化 V ( G , D ∗ ) , 就是求解分布 P d a t a , P G 的 V(G,D^*),就是求解分布P_{data},P_{G}的 V(G,D∗),就是求解分布Pdata,PG的js divergence,所以训练一个判别器,就是通过 P d a t a P_{data} Pdata, P G P_{G} PG sample出来的样本去求这两个分布的差异。
3. RMSProp 算法
RMSProp 是一种优化算法,用于在机器学习中自适应地调整学习率。它是Adagrad算法的改进版本,用于解决Adagrad算法可能出现的学习率过于下降的问题。与Adagrad算法不同,RMSProp算法引入了一个衰减系数 α \alpha α,用来控制梯度平方累加项的贡献程度。具体而言,给定一个优化目标和一组参数。
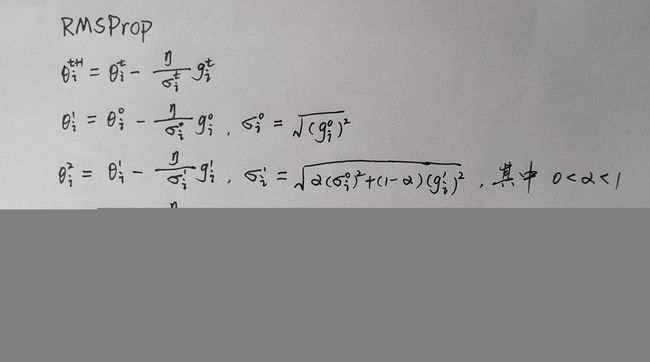

RMSProp算法的步骤如下:
- 初始化累计梯度平方的初始值为零,记为 σ i t − 1 \sigma^{t-1}_{i} σit−1。
- 初始化衰减系数 α \alpha α 为一个小的常数(如0.9)。
- 对于每个训练样本,计算参数的梯度 g i t g^{t}_{i} git。
- 更新累计梯度平方: σ i t \sigma^{t}_{i} σit = α \alpha α × σ i t − 1 \sigma^{t-1}_{i} σit−1 + (1 - α \alpha α) × ( g i t ) 2 (g^{t}_{i})^{2} (git)2。
- 根据公式计算每个参数的学习率:学习率 = η σ t \frac{\eta}{\sigma^{t}} σtη,其中 σ t \sigma^{t} σt是为了数值稳定性而加入的小值,随梯度的改变而改变。
- 根据学习率和梯度更新参数的值:参数 = 参数 - 学习率 × 梯度。
RMSprop代码实现
def _single_tensor_rmsprop(
params: List[Tensor],
grads: List[Tensor],
square_avgs: List[Tensor],
grad_avgs: List[Tensor],
momentum_buffer_list: List[Tensor],
*,
lr: float,
alpha: float,
eps: float,
weight_decay: float,
momentum: float,
centered: bool,
maximize: bool,
differentiable: bool,
):
for i, param in enumerate(params):
grad = grads[i]
grad = grad if not maximize else -grad
square_avg = square_avgs[i]
if weight_decay != 0:
grad = grad.add(param, alpha=weight_decay)
is_complex_param = torch.is_complex(param)
if is_complex_param:
param = torch.view_as_real(param)
grad = torch.view_as_real(grad)
square_avg = torch.view_as_real(square_avg)
square_avg.mul_(alpha).addcmul_(grad, grad, value=1 - alpha)
if centered:
grad_avg = grad_avgs[i]
if is_complex_param:
grad_avg = torch.view_as_real(grad_avg)
grad_avg.mul_(alpha).add_(grad, alpha=1 - alpha)
avg = square_avg.addcmul(grad_avg, grad_avg, value=-1).sqrt_()
else:
avg = square_avg.sqrt()
if differentiable:
avg = avg.add(eps)
else:
avg = avg.add_(eps)
if momentum > 0:
buf = momentum_buffer_list[i]
if is_complex_param:
buf = torch.view_as_real(buf)
buf.mul_(momentum).addcdiv_(grad, avg)
param.add_(buf, alpha=-lr)
else:
param.addcdiv_(grad, avg, value=-lr)
总结
学习 Transformer 让我深刻认识到了注意力机制的重要性,可以帮助模型更好地处理文本序列中的长距离依赖关系。相比于传统的循环神经网络和卷积神经网络,Transformer 在处理自然语言处理任务的时候得到了很好的效果。除了注意力机制,Transformer 还使用了残差连接、层归一化和位置编码等技术,这些技术在提高模型的性能和稳定性方面发挥了很大的作用。此外,Transformer 的模型结构非常清晰、简洁,便于理解和实现。此外,Transformer 还有许多变体和扩展,如 GPT 系列、BERT、Transformer-XL 等,它们不断推动着自然语言处理领域的发展。
总之,学习 Transformer 让我对自然语言处理、深度学习和模型设计等方面有了更深的理解和认识,也让我对今后的学习和研究有了更多的启示。