矩阵快速幂学习笔记

其实会用快速幂已经有好长一阵子了，但是一直没有写一篇入门快速幂的笔记。

据说，在递推式优化上具有神奇的效果（效率很高）

 

两矩阵相乘，朴素算法的复杂度是O(N^3)。如果求一次矩阵的M次幂，

按朴素的写法就是O(N^3*M)。既然是求幂，不免想到快速幂取模的算法，

这里有快速幂取模的介绍，a^b %m 的复杂度可以降到O(logb)。

如果矩阵相乘是不是也可以实现O(N^3 * logM)的时间复杂度呢？答案是肯定的。

　　先定义矩阵数据结构：　

struct Mat {

    double mat[N][N];

};

　　O(N^3)实现一次矩阵乘法

Mat operator * (Mat a, Mat b){

    Mat c;

    memset(c.mat, 0, sizeof(c.mat));

    for(int k = 0; k < n; ++k){

        for(int i = 0; i < n; ++i){

            if(a.mat[i][k] <= 0)    continue;   //

            for(int j = 0; j < n; ++j){

                if(b.mat[k][j] <= 0)    continue;   //

                c.mat[i][j] += a.mat[i][k] * b.mat[k][j];

            }

        }

    }

    return c;

}

　　矩阵的幂运算（非常简短）

Mat operator ^ (Mat a, int k){

    Mat c;

    for(int i = 0; i < n; ++i){

        for(int j = 0; j < n; ++j){

            c.mat[i][j] = (i == j); //init

        }

    }

    for(; k; k >>= 1){

        if(k & 1)   c = c * a;  //key, 这里需要理解一下为什么奇数时候要乘

        a = a * a;

    }

    return c;

}

　　

如果还不太懂的话， 可以举个例子:

　　求第n个Fibonacci数模M的值。如果这个n非常大的话，普通的递推时间复杂度为O(n)，

　　这样的复杂度很有可能会挂掉。这里可以用矩阵做优化，复杂度可以降到O(logn * 2^3)

如图：

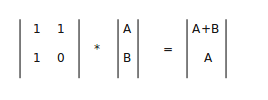 A = F(n - 1), B = F(N - 2)，

这样使构造矩阵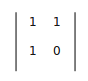的n次幂乘以初始矩阵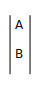得到的结果就是。

因为是2*2的据称，所以一次相乘的时间复杂度是O(2^3)，总的复杂度是O(logn * 2 ^ 3 + 2 * 2 * 1 )

 

接下来贴一道题目：zoj 2853 Evolution.