深度学习 PyTorch_Week1【任务2】张量操作与线性回归

一、张量的操作：拼接、切分、索引和变换

张量拼接与切分

1.1 torch.cat()

功能：将张量按维度dim进行拼接

• tensors：张量序列
• dim：要拼接的维度

代码实现：

t = torch.ones((2, 3))

t_0 = torch.cat([t, t], dim=0)
t_1 = torch.cat([t, t, t], dim=1)

print("t_0:{} shape:{}\nt_1:{} shape:{}".format(t_0, t_0.shape, t_1, t_1.shape))

结果：

t_0:tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]]) shape:torch.Size([4, 3])
t_1:tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1., 1.]]) shape:torch.Size([2, 9])

1.2 torch.stack()

功能：在新创建的维度dim上进行拼接

• tensors：张量序列
• dim：要拼接的维度
  

1.1与1.2皆为将张量拼接起来的方法，但两者稍稍不同的地方是.cat不会扩张张量的维度，而.stack会扩张张量的维度

代码实现：

t = torch.ones((2, 3))
t_stack = torch.stack([t, t], dim=2)
print("\nt_stack:{} shape:{}".format(t_stack, t_stack.shape))

结果：

我们创建一个2*‘3的张量，由于我们指定第二维度进行拼接，即dim=2，而我们的张量只有0与1两个维度，所以会在第二维度上创建一个维度，然后在这个维度上进行拼接，如图，即得到了2*3‘*2的张量。

实现代码：

t = torch.ones((2, 3))
t_stack = torch.stack([t, t, t], dim=0)
print("\nt_stack:{} shape:{}".format(t_stack, t_stack.shape))

结果：

我们创建一个2 *3的张量，若指定第0维度，由于已经有了第0维度，所以其会把原有的维度往后挪一个维度，在第0维度创建了一个新的维度，在其上进行拼接，生成3 *2 *3维张量。

1.3 torch.chunk()

功能：将张量按维度dim进行平均切分

返回值:张量列表

注意事项：若不能整除，最后一份张量小于其他张量

• input：要切分的张量
• chunks：要切分的份数
• dim：要切分的维度
  

代码实现：

a = torch.ones((2, 5))  # 7
list_of_tensors = torch.chunk(a, dim=1, chunks=2)   # 3

for idx, t in enumerate(list_of_tensors):
    print("第{}个张量：{}, shape is {}".format(idx+1, t, t.shape))

结果：

把第1维度切分成两份，由于5除以2不能整除，故且分为3与2，最后一份为2
具体计算为5除2向上取整
若是7分为3份，则为3，3，1

1.4 torch.split()

功能：将张量按维度dim进行切分（比chunk更强大一些，可以指定切分的长度）

返回值：张量列表

• tensor：要切分的张量
• split_ size_ or_ sections：为int时，表示每一份的长度；为list时， 按list元素切分
• dim：要切分的维度
  
  int代码实现：

t = torch.ones((2, 5))

list_of_tensors = torch.split(t, 2, dim=1)  # [2 , 1, 2]

for idx, t in enumerate(list_of_tensors):
    print("第{}个张量：{}, shape is {}".format(idx+1, t, t.shape))

结果：

list代码实现：

t = torch.ones((2, 5))

list_of_tensors = torch.split(t, [2, 1, 2], dim=1)
for idx, t in enumerate(list_of_tensors):
    print("第{}个张量：{}, shape is {}".format(idx, t, t.shape))

结果：

张量索引

2.1 torch.index_ select()

功能：在维度dim上，按index索引数据

返回值：依index索引数据拼接的张量

• input：要索引的张量
• dim：要索引的维度
• index：要索引数据的序号
  
  代码实现：

t = torch.randint(0, 9, size=(3, 3))  # 创建3*3均匀分布
idx = torch.tensor([0, 2], dtype=torch.long)    # 注意这里是长整型数据类型，使用float会报错
t_select = torch.index_select(t, dim=0, index=idx)  # 索引t中维度0的第0和第2个张量
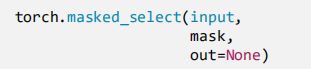
print("t:\n{}\nt_select:\n{}".format(t, t_select))

结果：

2.2 torch.masked_select()

功能：按mask中的True进行索引 （通常这个方法用来筛选数据）

返回值：一维张量（因为不能确定mask中True元素的个数，所以不能确定返回的张量的形状，因此返回一维张量）

• input：要索引的张量
• mask：与input同形状的布尔类型张量
  

代码实现：

t = torch.randint(0, 9, size=(3, 3))
mask = t.ge(5)  # ge is mean greater than or equal/   gt: greater than  le  lt
t_select = torch.masked_select(t, mask)
print("t:\n{}\nmask:\n{}\nt_select:\n{} ".format(t, mask, t_select))

ge(5)表示大于等于5，gt表示大于，le表示小于等于 lt表示小于
结果：

张量变换

3.1 torch.reshape()

功能：变换张量形状
注意事项：当张量在内存中是连续时，新张量与input共享数据内存

• input：要变换的张量
• shape：新张量的形状
  

代码实现：

t = torch.randperm(8)   # 生成0-7的随机排列
t_reshape = torch.reshape(t, (2, 4))    # 与t_reshape = torch.reshape(t, (-1, 4))等价
print("t:{}\nt_reshape:\n{}".format(t, t_reshape))

# 验证内存共享
t[0] = 1024
print("t:{}\nt_reshape:\n{}".format(t, t_reshape))
print("t.data 内存地址:{}".format(id(t.data)))
print("t_reshape.data 内存地址:{}".format(id(t_reshape.data)))

结果：

过程中，常常遇到t_reshape = torch.reshape(t, (-1, 4))中 -1这个参数，它表示这个维度不需要关心具体是多长，它是根据别的维度去计算而来。
t_reshape = torch.reshape(t, (-1, 2, 2))与t_reshape = torch.reshape(t, (2, 2, 2))等价

3.2 torch.transpose()

功能：交换张量的两个维度 （经常在图像前期的预处理中运用，有时我们读入的图像是chanel * h * w，需要把它变换成h *w *c）

• input：要变换的张量
• dim0：要交换的维度
• dim1：要交换的维度
  

代码实现：

t = torch.rand((2, 3, 4))
t_transpose = torch.transpose(t, dim0=1, dim1=2)    # c*h*w     h*w*c
print("t shape:{}\nt_transpose shape: {}".format(t.shape, t_transpose.shape))

结果：

3.3 torch.t()

功能：2维张量转置，对矩阵而言，等价于torch.transpose(input, 0，1)

3.4 torch.squeeze()

功能：压缩长度为1的维度(轴)

• dim：若为None，移除所有长度为1的轴；若指定维度，当且仅当该轴长度为1时，可以被移除；
  

代码实现：

t = torch.rand((1, 2, 3, 1))
t_sq = torch.squeeze(t)
t_0 = torch.squeeze(t, dim=0)   # 去掉指定维度
t_1 = torch.squeeze(t, dim=1)
print(t.shape)
print(t_sq.shape)
print(t_0.shape)
print(t_1.shape)

结果：

3.5 torch.unsqueeze()

功能：依据dim扩展维度

• dim：扩展的维度
  

二、张量的数学运算

加减乘除，对数 指数 幂函数，三角函数

torch.add()

功能：逐元素计算input+alpha*other

• input：第一个张量
• alpha：乘项因子
• other：第二个张量
  

Pythonic：
这两种方法在优化时会使用到
torch. addcdiv()

torch.add cmul()

代码实现：

t_0 = torch.randn((3, 3))
t_1 = torch.ones_like(t_0)
t_add = torch.add(t_0, 10, t_1)

print("t_0:\n{}\nt_1:\n{}\nt_add_10:\n{}".format(t_0, t_1, t_add))

结果：

三、线性回归

线性回归是分析一个变量与另外一(多)个变量之间关系的方法

因变量：y
自变量：x
关系：线性
y=wx+b
分析：求解w, b

求解步骤：
1.确定模型 Model: y=wx + b
2.选择损失函数 MSE:

3.求解梯度并更新w,b
w=w-LR* w.grad LR为学习率 步长
b=b-LR* w.grad
不断地迭代更新w,b 使得损失函数达到最小，停止迭代更新

一元线性回归模型的更新迭代过程：蓝色是数据点，x轴是自变量，因变量就是y轴，红色是线性回归模型。由于这里是一元线性回归，所以它是一条直线。
更新过程，首先，初始化参数w,b，得到一条原始的直线，之后计算Loss，根据Loss来更新w,b，最终红色直线接近蓝色点。
可以看到，随着迭代次数不断更新，在迭代第100次时，Loss是0.7，是比较低的，得到一条接近蓝点的曲线，也就是我们的线性模型。

代码实现：

import torch
import matplotlib.pyplot as plt
torch.manual_seed(10)

lr = 0.05  # 学习率    20191015修改

# 创建训练数据
x = torch.rand(20, 1) * 10  # x data (tensor), shape=(20, 1)  # 创建20个数据点
y = 2*x + (5 + torch.randn(20, 1))  # y data (tensor), shape=(20, 1) # y=2x+5+噪声

# 构建线性回归参数
w = torch.randn((1), requires_grad=True)  # w通过正态分布进行初始
b = torch.zeros((1), requires_grad=True)  # b初始化为0 要用到自动梯度求导，故requires_grad=True

for iteration in range(1000):

    # 前向传播
    wx = torch.mul(w, x)
    y_pred = torch.add(wx, b)  # y为预测值

    # 计算 MSE loss
    loss = (0.5 * (y - y_pred) ** 2).mean()

    # 反向传播
    loss.backward()  # 自动求导系统 可以得到梯度

    # 更新参数
    b.data.sub_(lr * b.grad)  # grad是来存储梯度的
    w.data.sub_(lr * w.grad)

    # 清零张量的梯度   20191015增加
    w.grad.zero_()
    b.grad.zero_()

    # 绘图
    if iteration % 20 == 0:

        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=5)
        plt.text(2, 20, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.xlim(1.5, 10)
        plt.ylim(8, 28)
        plt.title("Iteration: {}\nw: {} b: {}".format(iteration, w.data.numpy(), b.data.numpy()))
        plt.pause(0.5)

        if loss.data.numpy() < 1:   # 设置停止条件 Loss<1时，停止迭代更新
            break

结果：





遇到问题：程序运行出现问题

明明安装了matplotlib，为何运行还是出现错误ModuLeNotFoundError: NO module named ’ matplotlib '？
project用的虚拟环境，而matplotlib包安装在了base的环境里，未在同一环境中
解决方法：
在cmd命令行中先输入activate pytorch_cpu（虚拟环境）进入这个虚拟环境，再pip install matplotlib 如图