Unity3D中的线性插值Lerp()函数解析

介绍

在Unity中，大部分人在做摄像机跟随、人物移动等情况时都会用到Lerp这个函数，**至于底层是怎么实现的呢？**我之前可能还停留在使用的阶段，最近有个刚入门的小白问我引发了我的思考，发现自己只停留在使用的阶段没有真正的理解，当我明白了底层之后发现原来底层并不是那么可怕，看完这篇文章希望你有所收获。

Lerp的方法

1.Mathf.Lerp(float a,float b,float t)

实际上就是对[a,b]值域取t比例算出的差值

举例:

∵取值Math.Lerp(0,10,0.1) 用Unity输出发现是取值1

∴把上述转换成直线取代帮助理解，如图所示：

将Mathf.Lerp(0,10,0.1)理解为 AB线段长为10，已知AC为0.1AB，求线段AC长度

∵AC = AB*0.1
   AB = 10
∴AC = 10 * 0.1 
   AC = 1

如果有负数我们也可以将其值域算出来一样的算法，
总结一下可以推导出
Mathf.Lerp(float a,float b,float t)的底层实现为 a+(b-a)*t

工具类

public static class MathVirtual
	{
    	public static float Lerp(float a,float b,float t)
    	{
    		if (t <= 0)
        	{
            	return a;
        	}
        	else if(t >= 1)
        	{
            	return b;
        	}
        	return a + (b - a) * t;
    	}
	}

2.Vector2.Lerp(Vector2 a,Vector2 b,float t)

实际同Mathf.Lerp(a,b,t)一样，只是将其装换成二维坐标

举例:

把上述转换成二维坐标系取代帮助理解，如图所示：

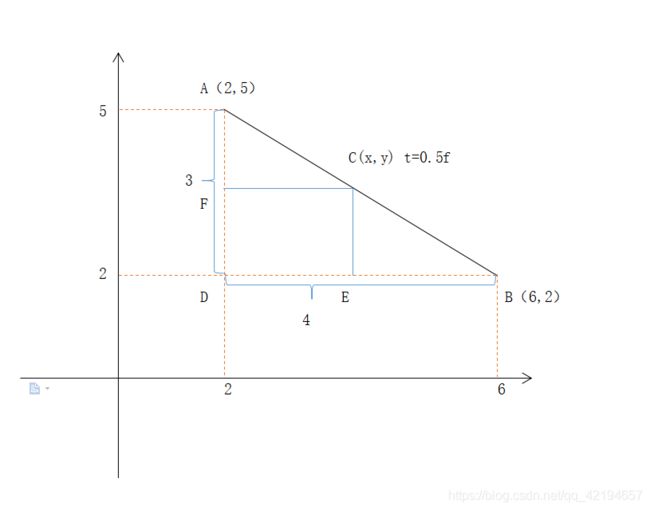
如图所知已知条件 ：AD = 3 ， DB = 4 ，CE⊥DB ，DF⊥AD ，AD⊥DB ，AC = BC

答：

∵CE⊥DB  
AD⊥DB
∴∠ADB = ∠ECB = 90°
∵∠ABC = ∠ABC
∠ADB = ∠ECB = 90°
∴△ADB∽△CEB
∵AC = BC
∴AB=2CB
∵△ADB∽△CEB
AB=2CB
∴DB = 2EB = 4
EB = DE = 2
C点的x = 2 + 2 = 4
同理△AFC  ∽ △ADB
AF=FD = 3/2 = 1.5
∴C点的y = 2 + 1.5 = 3.5
C（4，3.5）

如下图：

由此推理出我们的猜想是正确的。

补充工具类

	/// 

    /// float插值运算
    /// 
    /// 最小值
    /// 最大值
    /// 差值
    /// float
    public static float Lerp(float a,float b,float t)
    {
        if (t <= 0)
        {
            return a;
        }
        else if(t >= 1)
        {
            return b;
        }
        return a + (b - a) * t;
    }
    
    /// 

    /// 二维插值运算
    /// 
    /// 最小值
    /// 最大值
    /// 差值
    /// Vector2
    public static Vector2 Lerp(Vector2 a,Vector2 b,float t)
    {
        return new Vector2(Lerp(a.x,b.x,t),Lerp(a.y,b.y,t));
    }

3.Vector3.Lerp(Vector3 a,Vector3 b,float t)

在Unity开发过程中这个函数可能用到的是最多的，原理其实跟Vector2的原理是一样的，只是从二维坐标转换成三维空间坐标，比Vector2多了一个Z轴而已。

例子就不拿出来了，验证过是没有问题的，直接讲一下原理。
这里的例子直接拿鹏哥的博客中的例子讲解，他的例子说的也是非常明白，看完收获颇多。

求C点坐标X的值

这里的已知条件为A(0,10,0)，B(10,0,-10)，AC/AB = 0.4
根据相似图形对应边成比例的初中几何知识可知

∵⊿ABO中AC/AB=OD/OB
同理在⊿OBF中OD/OB=OE/OF
∴AC/AB=OD/O=OE/OF = 0.4
C点的X坐标值为：OE=0.4*OF=0.4*10=4

求C点坐标Y的值

∵EO/AO=DF/AF=CB/AC=1-0.4=0.6
同理C点的Y坐标值EO=0.6*AO=0.6*10=6。

综上所述，C点的三维坐标为C(4,6,-4)

补充工具类

    /// 

    /// float插值运算
    /// 
    /// 最小值
    /// 最大值
    /// 差值
    /// float
    public static float Lerp(float a,float b,float t)
    {
        if (t <= 0)
        {
            return a;
        }
        else if(t >= 1)
        {
            return b;
        }
        return a + (b - a) * t;
    }
    
    /// 

    /// 二维插值运算
    /// 
    /// 最小值
    /// 最大值
    /// 差值
    /// Vector2
    public static Vector2 Lerp(Vector2 a,Vector2 b,float t)
    {
        return new Vector2(Lerp(a.x,b.x,t),Lerp(a.y,b.y,t));
    }

    /// 

    /// 三维插值运算
    /// 
    /// 最小值
    /// 最大值
    /// 差值
    /// Vector2
    public static Vector3 Lerp(Vector3 a, Vector3 b, float t)
    {
        return new Vector3(Lerp(a.x, b.x, t), Lerp(a.y, b.y, t), Lerp(a.z, b.z, t));
    }

总结

Vector4.Lerp(Vector4 a,Vector4 b,float t)
Color.Lerp(Color a,Color b,float t)
Material.Lerp(Material a,Material b,float t)

原理都是相同的，有兴趣可以自己去尝试一下去补充工具类。