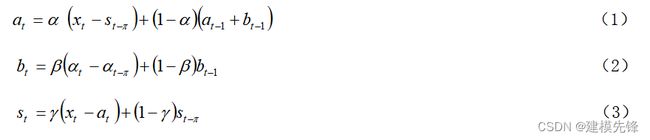时序预测：LSTM、ARIMA、Holt-Winters、SARIMA模型的分析与比较

基于Python的入门级时间序列预测分析

目录

引言

1 数据描述

2 理论模型简述

2.1 Holt-Winters 三参数指数平滑模型表

2.2 ARIMA模型

2.3 SARIMA模型

2.4 LSTM模型

3 数据检验与分解

3.1 单位根检验

3.2 序列分解

4 建立时间序列模型

4.1 模型识别

4.2 ARIAM模型

4.2.1 ARIMA(3,1,3)模型拟合

4.2.2 参数估计和模型检验

5 模型比较与预测

5.1 三参数指数平滑模型拟合

5.2 ARIMA(3,1,3)模型拟合

5.3 SARIMA模型拟合

5.4 LSTM模型拟合

5.5 模型对比

5.6 SARIMA模型预测

5.6.1 参数估计和模型检验

5.6.2 模型预测

5 模型比较与预测

补充：

---

引言

近年来，民航旅客周转量一直是衡量国家或地区民航运输总量的重要指标之一。为了揭示民航旅客周转量背后的规律和趋势，本研究旨在综合分析1990年至2023年的相关数据。

通过单位根检验和序列分解，我们确定了民航旅客周转量数据的非平稳性，并采用ARIMA模型进行建模和拟合。在模型选择过程中，我们比较了Holt-Winters三参数指数平滑模型、SARIMA模型和LSTM模型的拟合效果，以确定最佳的预测模型。

1 数据描述

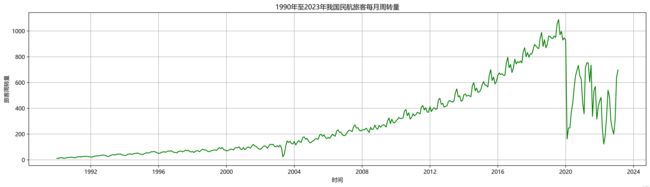
根据1990-2023年的我国民航旅客周转量的月统计资料，绘制其趋势图如图所示。

from dateutil.parser import parse
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei')
import seaborn as sns
import numpy as np
import pandas as pd

 
# 民航旅客周转量_当期
df = pd.read_csv('中国航空数.csv')  # a10
df.head()


date	value
0	1990-01	12.61
1	1990-02	9.67
2	1990-03	16.32
3	1990-04	15.87
4	1990-05	16.47

# Draw Plot
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei')
def plot_df(df, x, y, title="", xlabel='时间', ylabel='旅客周转量', dpi=800):
    plt.figure(figsize=(20,5), dpi=dpi)
    plt.plot(x, y, color='green')
    plt.grid()
    plt.gca().set(title=title, xlabel=xlabel, ylabel=ylabel)
    plt.show()
 
 
plot_df(df, x=df.index, y=df.value, title='1990年至2023年我国民航旅客每月周转量')

为了更好观察民航旅客周转量的季度变化趋势，绘制民航旅客周转量的年度趋势箱线图和月度趋势箱线图如图所示。

我们可以明显地看出旅客周转量具有季节波动趋势，由于第一季中的春运结束，旅客周转量会到第二季度有明显的下降趋势；第三季度的数据7、8月份暑假是旅客周转量的高峰，然后九月又有下降趋势；第四季度的10月为国庆黄金周，旅客周转量有明显上升趋势，然后下降到季度末尾，迎来春运又呈现出上升趋势。

2 理论模型简述

2.1 Holt-Winters 三参数指数平滑模型表

Holt-Winters三参数指数平滑模型通过考虑数据的趋势、季节性和平稳成分来进行预测。它使用三个参数：平滑系数（smoothing coefficients）α、β和γ，分别用于平滑数据的级别（level）、趋势（trend）和季节性（seasonality）。这些平滑操作使得模型能够适应数据的变化，并预测未来的趋势和季节性变动。

基于加法的Holt-Winters季节模型，其三参数指数平滑模型的构造如下所示：

基于乘法的Holt-Winters季节模型，其三参数指数平滑模型的构造如下所示：

2.2 ARIMA模型

ARIMA（Autoregressive Integrated Moving Average）模型是一种常用的时间序列分析和预测方法。它结合了自回归（AR）模型、差分（I）和移动平均（MA）模型的特点，用于捕捉数据的自相关性、趋势性和季节性。具有如下结构的模型成为求和自回归移动平均模型，简记为ARIMA(p,d,q)模型：

ARIMA模型的建立通常包括三个主要步骤：确定模型阶数、估计模型参数和模型诊断。首先，确定模型的阶数。ARIMA模型由p、d和q三个参数组成，分别代表自回归阶数（AR）、差分阶数（I）和移动平均阶数（MA）。通过观察时间序列数据的自相关图（ACF）和偏自相关图（PACF），可以初步确定模型的阶数。第二步是估计模型参数。使用最大似然估计（Maximum Likelihood Estimation）等方法，根据历史数据对AR、I和MA的参数进行估计。这些参数反映了数据的自相关性、趋势性和季节性的影响程度。

最后一步是模型诊断。通过对残差序列进行检验，判断模型的拟合效果和残差序列是否符合模型假设。常用的诊断方法包括检查残差的自相关性、白噪声检验、残差的正态性等。ARIMA模型可以应用于各种类型的时间序列数据，包括经济数据、气象数据、股票价格等。它可以用于预测未来的数值、分析数据的趋势和季节性，并对数据进行平滑处理。

2.3 SARIMA模型

SARIMA（Seasonal Autoregressive Integrated Moving Average）模型是在ARIMA模型的基础上添加了季节性成分的一种时间序列分析和预测方法。它用于处理具有明显季节性模式的数据。其模型的数学表示如下：

其中，小写字母p、d和q分别表示非季节性自回归、差分和移动平均项的阶数，而大写字母P、D、Q和s分别表示季节性自回归、差分、移动平均项的阶数和季节性周期的长度。SARIMA模型的表达式可以分为两个部分：非季节性部分和季节性部分。

非季节性部分：

其中，Yₜ表示时间序列的观测值，B是向后滞后算子（Backshift Operator），εₜ是白噪声误差项，φ₁, φ₂, ..., φₚ和θ₁, θ₂, ..., θq分别是非季节性自回归和移动平均项的系数，p是自回归项的阶数，q是移动平均项的阶数，d是差分次数。

季节性部分：

其中，Bˢ是季节性向后滞后算子，Φ₁, Φ₂, ..., ΦPₚ和Θ₁, Θ₂, ..., ΘQₚ分别是季节性自回归和移动平均项的系数，P是季节性自回归项的阶数，Q是季节性移动平均项的阶数，D是季节性差分次数，s是季节性周期的长度。

2.4 LSTM模型

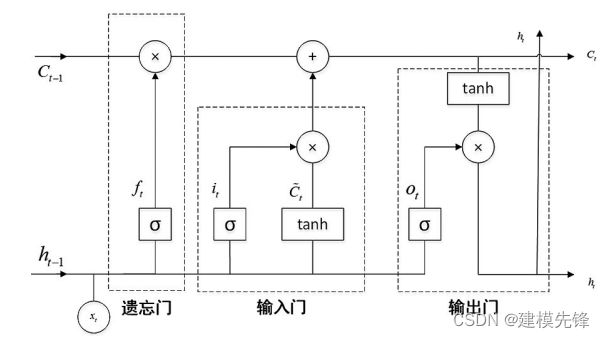
LSTM（Long Short-Term Memory）是一种常用于处理序列数据的深度学习模型，特别适用于处理具有长期依赖性的序列数据。它是一种循环神经网络（RNN）的变体，通过引入门控机制来有效地捕捉和记忆序列数据中的长期依赖关系。

LSTM模型的核心思想是利用门控单元来控制信息的流动和存储。如图所示，它包含三个关键的门控单元：遗忘门、输入门和输出门。

3 数据检验与分解

3.1 单位根检验

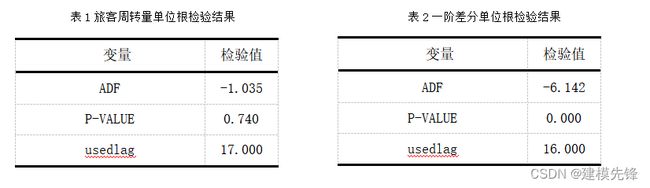
时间序列的平稳性是时间序列建模的重要前提。选用单位根ADF检验来判断民航旅客周转量时间序列的平稳性。

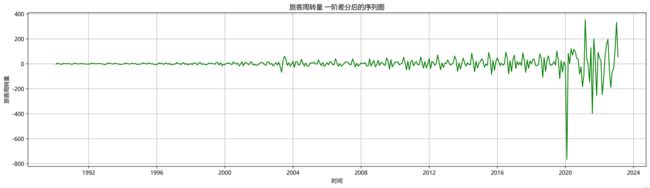
旅客周转量序列的ADF检验结果如表1所示，其P值为0.74，远大于0.05，故原数据为非平稳数据；而其一阶差分后的结果如表2所示，P值远小于0.05，接近0，故拒绝原假设，即一阶差分后的数据是平稳的时间序列数据，即为一阶单整模型，也确定了d=1。其一阶差分后的序列图如图所示。

3.2 序列分解

根据前面旅客周转量趋势图和旅客周转量季度趋势图综合观察，其序列变动随季节变化大致相等，每年有大致相等的增量，所以采用加法模型来分离长期趋势和季节变动。

旅客周转量序列其加法分解如图5所示，将时间序列数据分解为趋势、季节性和残差。可以明显的看出趋势一直处于不断上升的状态，对于季节性，十分明显在规律的间隔后能看出峰值，且频率为12个月，而残差从前期到后期的波动在一定范围。

4 建立时间序列模型

4.1 模型识别

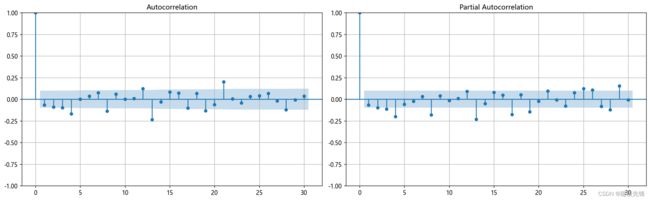
对旅客周转量序列一阶差分后的自相关和偏相关分析进行可视化，ACF图中在1阶后的自相关系数基本上都落在95%的置信区间上，p值取1；PACF图中，也在1阶后的偏相关系数基本上的落在95%的置信区间上，q取1。

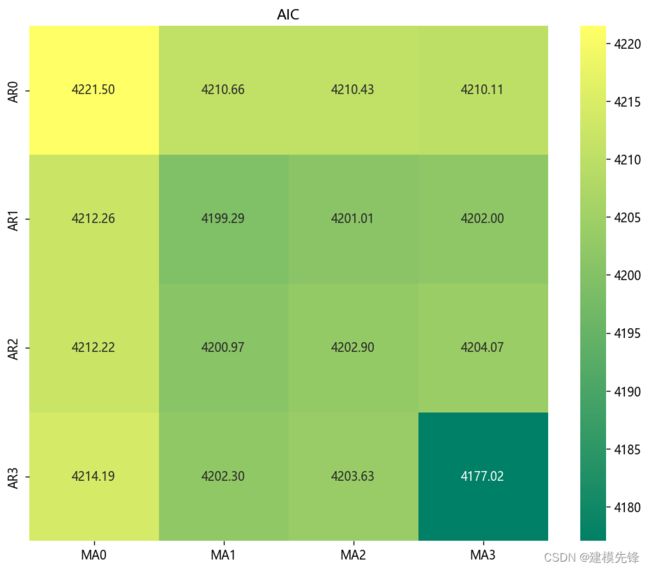
通过看图判断具有一定的主观性，通过遍历可能的参数选择统计量最小的模型相对更适合对数据的分析，把旅客周转量序列数据2021年前的数据划分为训练集，把2022年至今的数据划分为测试集，预测14期的数据，然后选择p从0-3,q从0-3,d=1，进行参数遍历拟合模型，采用AIC指标进行参数评估，得到结果如图所示：

采用AIC指标进行参数选择，得到最小的AIC值的组合为p=3,q=3,选择其作为模型进行拟合,因此针对原数据可知最终确定模型为ARIMA(3,1,3）。

4.2 ARIAM模型

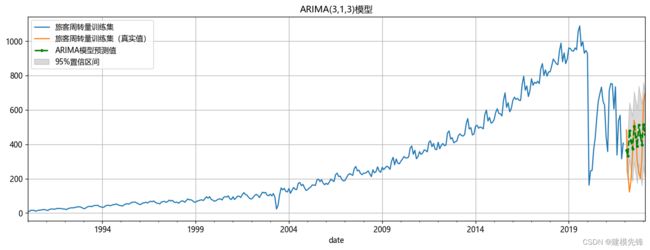
4.2.1 ARIMA(3,1,3)模型拟合

模型拟合效果良好。

4.2.2 参数估计和模型检验

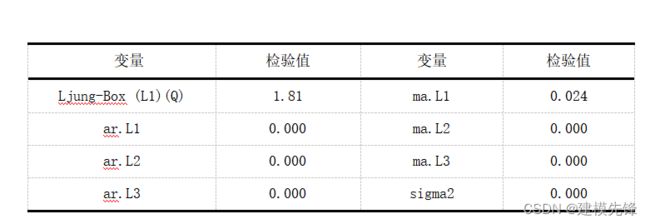
ARIAM(3,1,3)模型结果如表所示，一阶延迟下的LB统计量显著大于0.05，可以认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效。P>|z|列是对每个参数系数的检验。大部分参数的P值均小于0.05，所以在0.05的显著性水平下，拒绝原假设，模型中大部分参数的系数通过显著性检验。

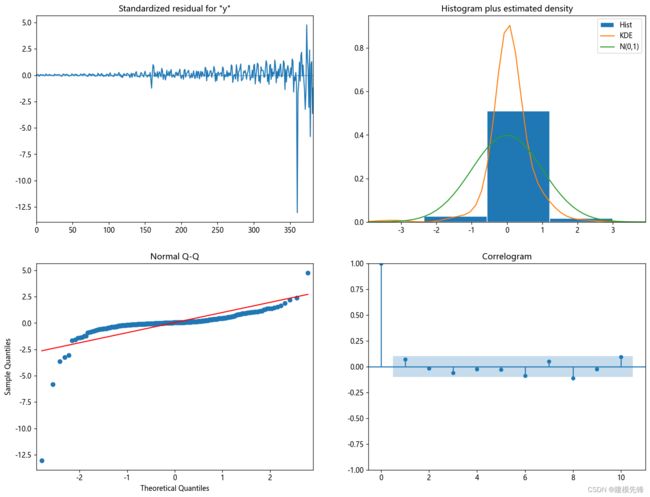
检验模型的残差是否满足均值为0，方差为常数的正太分布，结果如图所示：左上角为残差曲线，右下角为残差自相关图，其一阶后相关系数比较小；右上方的图绿色的线是标准正态分布N(0,1)，橙色的线是残差的分布情况，也可以通过左下方的QQ图来判断，残差趋近于正态分布，可以认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效。

综上分析，ARIMA(3,1,3)模型的拟合效果较好。

5 模型比较与预测

5.1 三参数指数平滑模型拟合

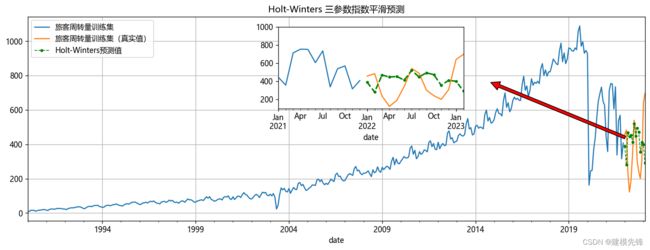
Holt-Winters 三参数指数平滑预测如图所示，其序列变动随季节变化大致相等，每年有大致相等的增量，所以采用加法模型，模型拟合得较好，既考虑了季节性波动，又考虑了趋势变化。

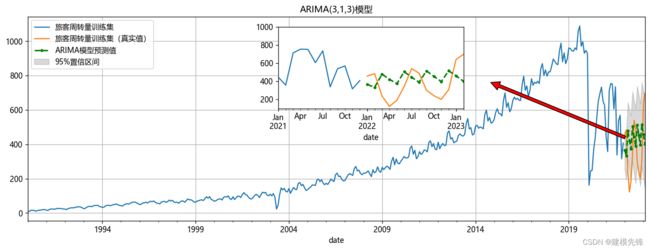
5.2 ARIMA(3,1,3)模型拟合

ARIMA模型在时间序列数据的拟合和预测中被广泛应用，它考虑了数据的自回归、差分和移动平均特性。通过对旅客周转量进行ARIMA(3,1,3)模型的拟合，可以获得较好的拟合效果和预测准确性。

5.3 SARIMA模型拟合

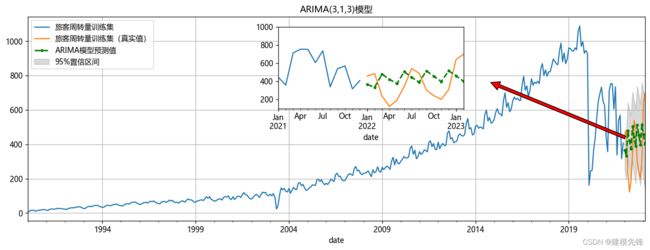为了更好地捕捉旅客周转量序列的季节性变化，引入了SARIMA模型。如图所示，SARIMA模型是ARIMA模型的扩展，加入了季节性因素的考虑。通过调整SARIMA模型的季节性参数，周期性参数设置为12，可以更准确地预测旅客周转量在不同季节的变化趋势。与ARIMA模型相比，SARIMA模型在拟合和预测上表现更加显著，能够更好地适应数据的季节性波动。

5.4 LSTM模型拟合

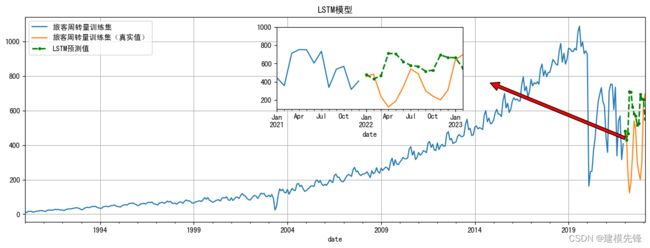旅客周转量的LSTM模型拟合如图所示，LSTM 主要是基于窗口滑动取数据训练来预测滞后数据，LSTM模型在此测试集上的预测较真实值偏高，拟合效果不如传统时间序列模型,其模型参数有待进一步优化。

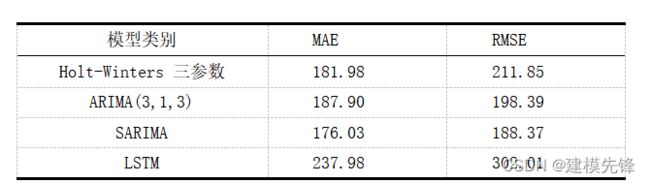
5.5 模型对比

模型对比如表所示，分别用Holt-Winters 三参数模型、ARIMA(3,1,3)模型、SARIMA模型、LSTM模型对旅客周转量序列数据进行拟合分析，加入季节性的SARIMA模型相比ARIMA模型的效果更好，SARIMA模型的AIC、MAE、RMSE均为最小，可见用SARIMA模型来对旅客周转量进行预测的效果最佳。SARIMA模型能够更准确地预测旅客周转量的变化，并提供可靠的决策依据。相比之下，Holt-Winters模型、ARIMA模型和LSTM模型在某些评估指标上表现稍逊一筹，但仍然具有一定的预测能力和应用价值。

5.6 SARIMA模型预测

5.6.1 参数估计和模型检验

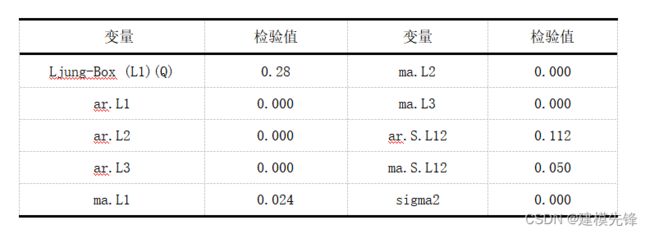
SARIMA模型参数如表所示，一阶延迟下的LB统计量大于0.05，可以认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效。大部分参数的P值均小于0.05，所以在0.05的显著性水平下，拒绝原假设，模型中大部分参数的系数通过显著性检验。

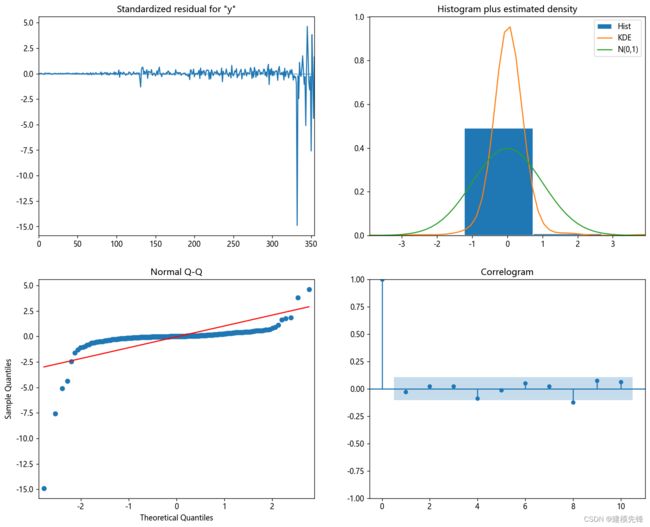
SARIMA模型残差检验结果如图所示：左上角为残差曲线，右下角为残差自相关图，其一阶后相关系数比较小；右上方的图绿色的线是标准正态分布N(0,1)，橙色的线是残差的分布情况，也可以通过左下方的QQ图来判断，残差趋近于正态分布，可以认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效。

由此，可以得出结论，SARIMAX(3，1，3)x(1，1，1，12)模型的拟合效果很好，可以帮助我们理解原始的时间序列数据并对未来的数值做出预测。

5.6.2 模型预测

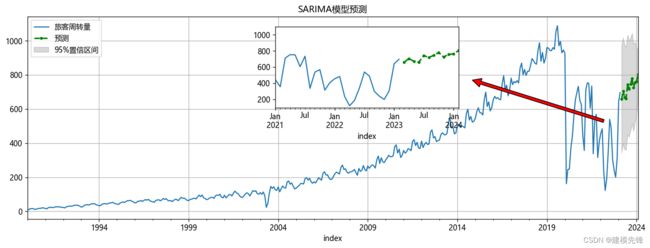
经过前面对民航旅客周转量数据的分析我们得到了SARIMA模型SARIMAX(3，1，3)x(1，1，1，12)，通过建立SARIMA模型对2023年2月后的12期进行预测，预测结果如下所示：

通过预测时序图可知，未来时间序列总体呈季节性波动趋势上升，未来12个月旅客周转量将缓速上升，具体预测数据如下表所示。这一趋势可能受到多种因素的影响，如节假日、旅游季节、经济状况等。

5 结论分析

本文首先对我国民航旅客周转量进行趋势分析，然后用ARIMA模型研究其变动趋势，在不考虑周期的影响下建立了ARIMA(3,1,3)模型，然后考虑其序列数据具有周期性波动，分别建立了Holt-Winters 三参数指数平滑模型和SARIMA模型进行分析，最后建立LSTM模型进行预测分析，通过模型的比较，得出加入周期性SARIMA模型在旅客周转量数据上的预测效果最好，并预测了未来12其的周转量数据。

虽然LSTM模型能够很好的捕捉序列之间的联系，但是可解释性没有传统模型好，传统模型的一个优势是模型参数可以得到不确定性估计，而对于模型预测的泛化能力，SARIMA和LSTM模型仍然有提升的空间，如果进一步优化，对于预测性能的提升，会有不错的效果。首先，可以进一步改进SARIMA模型和LSTM模型，提高它们在预测民航旅客周转量方面的准确性和鲁棒性。

其次，可以考虑使用其他的深度学习模型，如Transformer模型等，来进一步改善预测效果。此外，可以结合其他领域的数据和信息，如经济指标、航空运输政策等，来构建更加综合和准确的预测模型。最后，还可以研究民航旅客周转量与其他相关因素的关系，如旅游业发展、人口迁移等，以便更好地理解和预测旅客周转量的变化趋势。

补充：

AIC 和 BIC 这两个准则的定义与出发点不太一样，AIC是从预测角度，选择一个好的模型来预测，BIC是从拟合角度，选择一个对现有数据拟合最好的模型。

可能 AIC和BIC都计算了，且两个模型中，一个AIC小，另一个BIC小，时间序列参数选择是一门艺术，这种情况下可以比较变量的显著性，如果变量也都显著，那么两个模型都是对的，都可以用。

总的来说，参数的选择不能只评判 某一个指标，应该全方位的进行估评，结合aic bic 以及系数的显著性，结合来考虑，也就是说 存在几组参数都可以用的情况，不唯一，自己能阐明参数选择的理由就行。

理论部分 参考书籍

王燕. 时间序列分析基于R. 中国人民大学出版社.