李宏毅机器学习第二十三周周报 Flow-based model

week 23 Flow-based model

摘要

本文主要讨论了基于流的模型的。本文介绍了在之前介绍的几种模型的缺点，并引出了流模型。在此基础上，本文分别阐述了流模型的数学基础及模型的多种实现方式。其次本文展示了题为Density estimation using Real NVP的论文主要内容。这篇论文提出了Coupling layer以及Real NVP模型，该模型使用实值非体积保持变换（real-valued non-volume preserving transformation）。该文在四个数据集上进行实验，从数据角度证明了该网络的优越性。最后，本文基于pytorch实现了Seq2Seq（LSTM2LSTM）模型并用于预测ETTh数据集的后续结果。

Abstract

This article focuses on flow-based models. This article describes the shortcomings of several models described earlier and introduces the flow model. On this basis, this article expounds the mathematical basis of the flow model and the various implementation methods of the model. Secondly, this paper presents the main content of the paper entitled Density estimation using Real NVP. This paper proposes coupling layer and Real NVP model that uses a real-valued non-volume preserving transformation. This paper carries out experiments on four datasets, and the proves superiority of the network from the perspective of data. Finally, this article implements the Seq2Seq (LSTM2LSTM) model based on pytorch and uses to predict the subsequent results of the ETTh dataset.

一、李宏毅机器学习

1.引言

之前主要介绍了三种模型，component-by-component（Auto-regressive model）、VAE、GAN

component-by-component模型在不确定component顺序的情况下，效果较差，需要使用较长时间生成较短序列。VAE需要从下界开始优化，因此达到收敛的时间较长。GAN的训练过程不够稳定。

GAN：假定生成器G是一个神经网络，该网络定义了一个概率分布$p_G$。生成器G根据输入的简单分布$\pi (z)$生成分布$p_G(x)$，其中$x=G(z)$。其目标是生成尽可能类似真实分布样本$\{x^1,x^2,\dots ,x^{,}\}from{P}_{data}(x)$，即$G^{\ast }=arg{\max }_G{\sum }_{i=1}^m\log P_G(x^i)\approx arg{\min }_{g}KL(P_{data}||P_G)$。让真实分布与生成分布的似然性越大越好，亦即让真实分布与生辰分布之间的KL散度越小越好

但GAN并没有直接优化模型以达到目标函数，而流模型则针对这点进行了优化。

2.数学背景

Jacobian、Determinant、Change of Variable Theorem

2.1Jacobian

假定z通过映射f得到z，则其Jacobian矩阵为$J_f$，该矩阵由其偏导组成。相应的，其反函数的Jacobian矩阵是该矩阵的逆，即$J_f{J}_{f^{-1}}=I$
$$\begin{gathered} z=\left(\begin{array}{c}{z}_1\\ z_2\end{array}\right)x=\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right) \\ x=f(z) \\ {J}_f=\left(\begin{array}{c}\partial x_1/\partial z_1\partial x_1/\partial z_2\\ \partial x_2/\partial z_1\partial x_2/\partial z_2\end{array}\right) \\ {J}_{f^{-1}}=\left(\begin{array}{c}\partial z_1/\partial x_1\partial z_1/\partial x_2\\ \partial z_2/\partial x_1\partial z_2/\partial x_2\end{array}\right) \end{gathered}$$

2.2Determinant

即矩阵的行列式，其物理含义是一个矩阵在高维空间中的“体积”

2.3Change of Variable Theorem

假定有概率分布$\pi (z),p(x)$，映射$x=f(z)$，则如何求$p(x^{\prime }),\pi (z^{\prime })$之间的关系，其中$x^{\prime }=f(z^{\prime })$

首先考虑较为简单的情况，已知概率分布在其分布区间上的积分值为1，以下为两个区间上概率均匀分布的概率分布，若$x=f(z)=2z+1$，因为$p(x)$分布区间变大，那么其相较于$\pi (z)$在同样长度的分布区间上，前者的积分值更小。

以下考虑更复杂的一维情况，两个概率分布如下图，其不再均匀分布，而是由浅色曲线表示。在不知道两个分布的表达式，仅知道其采样的情况下，如何推导出其表达式的近似结果？

最终的目标是在映射关系下两个区间内两个概率分布的积分值相等，即蓝色方块面积等于绿色，$p(x^{\prime })\Delta x=\pi (z^{\prime })\Delta z$。作一定的变换有，拟合分布$p(x^{\prime })$即初始分布$\pi (z^{\prime })$与z对x微分绝对值的乘积。

tips：绝对值的原因是，微分的正负不影响结果，如下图左下角

接下来，考虑二维的情况，两个分布区间如下图所示，其中$p(x^{\prime })$的分布区间是两个二维向量的展开。根据前文，$p(x^{\prime })$分布区间的“体积”可由其变化量$\Delta x$所组成的行列式的值表示，从而有下图中公式

从而有如下推导

3.Flow-based Model

$$\begin{gathered} p(x^{\prime })|det(J_f)|=\pi (z^{\prime }) \\ p(x^{\prime })=\pi (z^{\prime })|det(J_{f^{-1}})| \end{gathered}$$

若使用GAN的框架，则有

为了便于计算，输入向量的size应当与输出向量的size相同，同时限定G的，相应的设置多个G以保证模型的复杂度。

按照上述方式设计神经网络，该网络的目标是将下式最大化
$$\log p_{J}K(x^i)=\log \pi (z^i)+\sum _{h=1}^K\log |det(J_{G_K^{-1}})|$$

首先考虑单个生成器的情况，训练时使用$G^{-1}$，训练完成用于生成时使用G

训练时从真实分布采样出$x^i$，经生成器处理，输出$z^i=G^{-1}(x^i)$

$log{p}_G(x^i)=log\pi (G^{-1}(x^i))+log|det(J_{G^{-1}})|$

当仅考虑第一项时，令$z^i$为零向量会得到最佳结果，但实际上受第二项影响，由于$det(J_{G^{-1}})=0$，第二项为负无穷，故受第二项调节，$z^i$非零向量。

coupling layer：处理前d维数据，使用F将前d维z转换为后续维度相同的向量，称${\beta }_i$，使用H将前d维z转换为后续维度相同的向量，称${\gamma }_i$，并直接将前d维z复制到x。用$\beta_i \odot $后续维度的z，在加上$\gamma_i$，最后得到后续的x。

当使用x进行计算时，前d维直接复制，后续维度$z_{z>d}=\frac{x_i-{\gamma }_i}{{\beta }_i}$

考虑上式的Jacobian矩阵，首先下图中蓝色箭头表示了各部分向量的对应关系，红色实线说明了该矩阵行列式的值为什么和反对角线的部分无关。

而在上图中已知x由z乘以$\beta$加上$\gamma$得到，显然各部分的偏导便是对应的$\beta$。因此右下角的矩阵是对角矩阵，同时Jacobian矩阵的计算如下图右下角。

将所有的coupling layer首尾相连构造一个神经网络，但该网络的前d维是没有发生变动的。因此按照下图中的方式构造神经网络，例如第一次将前d维复制，第二次将后d维复制，从而避免该问题。

当处理图像数据时，可以如下图左下角一样复制偶数部分的、计算奇数部分的；也可以如下图右上角，交替的复制部分的channel。

4.GLOW

[原论文][https://arxiv.org/abs/1807.03039]，[先导][https://arxiv.org/abs/1605.08803]，[论文概述][https://zhuanlan.zhihu.com/p/45732170]

作1*1卷积操作，使用一个可逆矩阵W将z转换为x，W可以用于打乱channel

当考虑仅有一次乘法时，对于$x=f(z)=Wz$，其Jacobian矩阵为W。当考虑整个图片时，其Jacobian矩阵如下图

二、文献阅读

1. 题目

题目：Density estimation using Real NVP

作者：Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio

链接：https://arxiv.org/abs/1605.08803

发布：Accepted at ICLR 2017

2. abstract

设计具有易于处理的学习、抽样、推理和评估模型有利于解决概率模型的无监督学习模型。作者使用实值非体积保持变换扩展了此类模型的空间，并通过抽样、对数似然评估和潜在变量操作证明了它在四个数据集上对自然图像进行建模的能力。

Designing models with tractable learning, sampling, inference and evaluation is crucial in solving unsupervised learning of probabilistic models. Authors extend the space of such models using real-valued non-volume preserving (real NVP) transformations, and demonstrate its ability to model natural images on four datasets through sampling, log-likelihood evaluation and latent variable manipulations.

3. 网络架构

3.1 change of variable formula

已知一观测数据——变量$x\in X$、一简单先验概率分布$p_Z$的采样数据——变量$z\in Z$，以及一双射$f:X\to Zwithg=f^{-1}$，现改变变量公式以定义一个模型分布$X$，如下式
$$p_X(x)=p_Z(f(x))|\text{det}(\frac{\partial f(x)}{\partial x^T})|\text{\hspace{1em}(2)}$$

$$\log (p_X(x))=\log (p_Z(f(x)))+\log (|\text{det}\frac{\partial f(x)}{\partial x^T}|)\text{\hspace{1em}(3)}$$

其中$\frac{\partial f(x)}{\partial x^T}$是f在x上的Jacobian

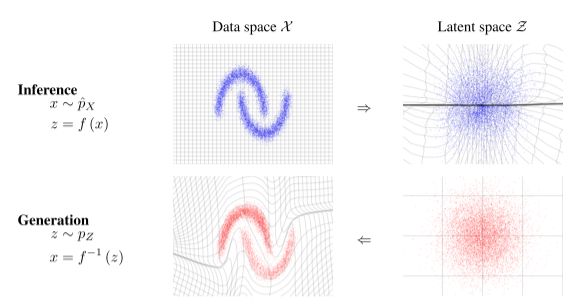
使用反变换规则可从结果分布中生成精确样本。在潜在空间中绘制一个样本$z\sim p_Z$，其逆像$x=f^{-1}(z)=g(z)$生成原始空间中的一个样本。计算点x上的密度是通过计算他的图像$f(x)$的密度并乘以相关的雅可比行列式$\frac{\partial f(x)}{\partial x^T}$完成的，详见图1

函数 f (x) 将左上角数据分布中的样本 x 映射到右上角潜在分布中的近似样本 z。这对应于给定数据的潜在状态的精确推断。反函数 f⁻¹ (z) 将右下角潜在分布中的样本 z 映射到左下角数据分布中的近似样本 x。这对应于从模型中精确生成样本。还针对 f (x) 和 f⁻¹ (z) 说明了 X 和 Z 空间中网格线的变换。

3.2 Coupling layers

直接使用Jacobian计算成本较高，故需要通过仔细设计函数，学习到一个双目标模型，该模型既灵活又易于处理。

建立一个灵活和易于处理的双射函数叠加一系列简单的 bijections。在每个简单的 bijections中，输入向量的一部分会使用一个函数来更新，这个函数的反变换很简单，但它以复杂的方式依赖于输入向量的其余部分，将这些简单的双射称为仿射耦合层。
$$y_{1:d}=x_{1:d}\text{\hspace{1em}(4)}$$

$$y_{d_1:D}=x_{d+1:D}\odot \exp (s(x_{1:d}))+t(x_{1:d})\text{\hspace{1em}(5)}$$

给定D维输入x和d$R^{d}x\to R^{D-d}$的函数，$\odot$是Hadamard乘积或者元素乘积，如下图

上图为正向和反向传播的计算图。耦合层应用一个简单的可逆变换，该变换包括缩放，然后根据输入向量 x1 的剩余部分向输入向量的一部分 x2 添加常量偏移。由于其简单的性质，这种变换既容易逆转，又具有易于处理的行列式。然而，函数 s 和 t 捕获的这种转换的条件性质显着增加了这个弱函数的灵活性。正向和反向传播操作具有相同的计算成本。

3.3Properties

3.4Masked convolution

分区可用二进制mask b实现，并使用下式构造y
$$y=b\odot x+(1-b)\odot (x\odot \exp (s(b\odot x))+t(b\odot x))\text{\hspace{1em}(9)}$$
本文使用了两个利用图像局部相关结构的分区: 空间棋盘图案和通道 mask ，如下图。当空间坐标的和为奇数时，空间棋盘图案 mask 的值为 1，否则为 0。通道 mask 的前半部分为 1，后半部分为 0。对于本文提出的模型， $s(\cdot ),t(\cdot )$是修正卷积网络

上图为仿射耦合层的掩蔽方案。左边是一个空间棋盘图案蒙版。右侧是通道屏蔽。压缩操作将 4 × 4 × 1 张量（左侧）缩小为 2 × 2 × 4 张量（右侧）。在挤压操作之前，使用棋盘图案来耦合层，而之后使用通道方式掩模图案。

3.5Combing coupling layers

可以通过交替模式组合耦合层来实现在不改变框架的情况下在整个过程中更新各部分参数，如下图。在这种交替模式中，在一次转换中保持相同的单元在下一次转换中被修改。

在这种情况下，雅可比行列式仍然是可处理的（式10、11），其逆运算也是可计算的（式12）。
$$\frac{\partial (f_b\circ f_a)}{\partial x_a^T}(x_a)=\frac{\partial f_a}{\partial x_a^T}(x_a)\cdot \frac{\partial f_b}{\partial x_b^T}(x_b=f_a(x_a))\text{\hspace{1em}(10)}$$

$$\text{det}(A\cdot B)=\text{det}(A)\text{det}(B)\text{\hspace{1em}(11)}$$

$$(f_b\circ f_a{)}^{-1}=f_a^{-1}\circ f_b^{-1}\text{\hspace{1em}(12)}$$

3.6Multi-scale architecture

本文使用压缩操作实现了一个多尺度体系结构 : 对于每个通道，它将图像分成形状为 2 × 2 × c 的子方块，然后将它们重塑为形状为 1 × 1 × 4c 的子方块。压缩操作将一个 s × s × c 张量转换成一个 s/2 × s/2 × 4c 张量(如下图)，有效地用空间大小交换通道的数量

在每个尺度上，将几个操作组合成一个序列: 首先应用三个具有交替棋盘 mask 的耦合层，然后执行一个压缩操作，最后再应用三个具有交替信道 mask 的耦合层。选择信道 mask，这样得到的分区就不会与之前的棋盘格 mask 冗余 。对于最终的比例，本文只应用 4 个交替棋盘格 mask 的耦合层。

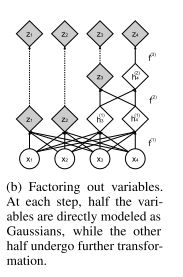
从计算和存储成本以及需要训练的参数数量来看，通过所有耦合层传播一个D维向量将是很麻烦的。出于这个原因，遵循[2]的设计选择，并以规则的间隔提出一半的维度(见公式14)。我们可以递归地定义这个操作(参见下图)

每层都执行上述耦合-挤压-耦合运算的顺序 (式14)。在每一层，随着空间分辨率的降低，s 和 t 中隐藏层特征的数量增加了一倍。将在不同尺度上提出的所有变量连接起来，得到最终的转换输出 (式16)。

因此，模型必须先高斯化在较细尺度上分解的单元 (在较早的一层中)，然后才高斯化在较粗尺度上分解的单元 (在较晚的一层中)。

此外，在较早的层中，高斯化和分解单元具有将损失函数分布到整个网络的实际好处，其原理类似于使用中间分类器引导中间层。它还显著减少了模型使用的计算量和内存，使网络能够训练更大的模型。
$$h^{(0)}=x\text{\hspace{1em}(13)}$$

$$(z^{(i+1)},h^{(i+1)})=f^{(i+1)}(h^{(i)})\text{\hspace{1em}(14)}$$

$$z^{(L)}=f^{(L)}(h^{(L-1)})\text{\hspace{1em}(15)}$$

$$z=(z^{(1)},\dots ,z^{(L)})\text{\hspace{1em}(16)}$$

此外，其在网络中使用批量正则化、权重正则化以正则化s和t。对整个耦合层输出应用批量归一化。批量归一化的影响很容易包含在雅可比行列式计算中，因为它充当每个维度上的线性重新缩放。也就是说，给定估计的批次统计量$\tilde{\mu },{\tilde{\sigma }}^2$，重定标函数
$$x\to \frac{x-\tilde{\mu }}{\sqrt{{\tilde{\sigma }}^2+ϵ}}\text{\hspace{1em}(17)}$$
其雅可比行列式为
$$(\prod _i({\tilde{\sigma }}_i^2+ϵ){)}^{-\frac{1}{2}}\text{\hspace{1em}(18)}$$
该方法除了可以用耦合层训练，还缓解了在通过基于梯度的方法使用尺度参数训练条件分布时经常遇到的不稳定问题

4. 文献解读

4.1 Introduction

无监督学习有潜力利用大量未标记的数据，并将这些进展扩展到其他不切实际或不可能的模式中。生成概率模型作为一种无监督学习方式能够创造新的内容，还具有广泛重建相关应用。本文通过引入real NVP 转换来建模高维、高度结构化的数据以应对该领域的挑战。本文提出的体系结构可以从该模型提取的层次特征中准确高效的重建输入图像。

4.2 创新点

1. 作者分析了过往概率生成模型的相关工作并进行了总结。

   即关于概率模型的相关工作都集中在使用最大似然方法训练模型上。

   • 概率无向模型利用二分结构的条件独立特性进行训练，从而对潜在变量进行有效的精确或者近似的后验推断。但由于潜在变量的相关边际分布的难解性，其在训练过程中所使用平均域推断、马尔科夫链、蒙特卡洛搜索等近似方法的收敛时间相较于复杂度较高的模型具有一定的不确定性，从而阻碍模型性能的提高。
   • 有向图形模型时根据原始抽样过程定义，其计算过程相对简单，但是缺乏无向模型的条件独立结构，这加大了潜在变量精确化和近似厚颜推断的难度。随机变分分析、平摊分析的最新结果允许通过最大化对数似然的变分下界来进行近似推理和深度有向图形模型的学习。

   GAN完全避免了最大似然原则，可以训练任意可微生成网络

2. 通过最大似然来解决在高维连续空间中学习高度非线性模型的问题

3. 引入了一种更灵活的架构——coupling layer，可以使用变量公式的变化来计算连续数据的对数似然

4.3 实验过程

作者在 CIFAR-10、 CelebA 、LSUNs、Imagenet 上进行了训练。 Imagenet上采样到 32 × 32 和 64 × 64 版本上进行训练，LSUN数据集对卧室、塔楼和教堂室外类别进行训练：对图像进行下采样，使最小边为 96 像素，并随机裁剪 64×64。对于 CelebA，使用相同的程序：采用 148 × 148 的近似中心裁剪，然后将其大小调整为 64 × 64。

多尺度架构会递归重复，直到最后一次递归的输入是 4 × 4 × c 张量。对于尺寸为 32 × 32 的图像数据集，使用 4 个残差块和 32 个隐藏特征图作为带有棋盘掩码的第一个耦合层。对于大小为 64 × 64 的图像，仅使用 2 个残差块。批量大小为 64。对于 CIFAR-10，我们使用 8 个残差块、64 个特征图，并且仅缩减一次。使用 ADAM和默认超参数进行优化，并对权重参数使用 L2 正则化，系数为 $5\cdot 10^{-5}$。

将先验 $p_Z$ 设置为各向同性单位范数高斯分布

在表中显示，每个维度的位数虽然没有比 Pixel RNN[3]有所改善，但与其他生成方法相比具有竞争力。

在潜在空间中，我们基于四个验证示例 z(1)、z(2)、z(3)、z(4) 定义流形，并通过两个参数$\varphi ,{\varphi }^{\prime }$进行参数化
$$z=cos(\varphi )(cos({\varphi }^{\prime })z_{(1)}+sin({\varphi }^{\prime })z_{(2)}+sin(\varphi ))(cos({\varphi }^{\prime })z_{(3)}+sin({\varphi }^{\prime })z_{(4)})\text{\hspace{1em}(19)}$$

4.4 结论

在本文中，定义了一类具有易于处理的雅可比行列式的可逆函数，从而实现精确且易于处理的对数似然评估、推理和采样。本文证明了，此类生成模型在样本质量和对数似然方面都实现了有竞争力的性能。

三、实验内容

1.任务概述

使用seq2seq模型预测电力负荷的时间序列，使用ETTh1.csv作为训练集，ETTh2.csv作为测试集。

2.数据集介绍

**数据内容：**该数据集通常包含有关电力系统的多种变量，如电力负荷、价格、天气情况等。这些变量可以用于预测未来的电力需求或价格。

时间范围和分辨率：数据通常按小时或天记录，涵盖了数月或数年的时间跨度。具体的时间范围和分辨率可能会根据数据集的版本而异。

数据集下载地址

3.模型参数

dataloader：

训练集尺寸: 12194 测试集尺寸: 2613 验证集尺寸: 2613
通过滑动窗口共有训练集数据： 12107 转化为批次数据: 756
通过滑动窗口共有测试集数据： 2526 转化为批次数据: 157
通过滑动窗口共有验证集数据： 2526 转化为批次数据: 157

参数设置：

parser = argparse.ArgumentParser(description=‘Time Series forecast’)
parser.add_argument(‘-model’, type=str, default=‘LSTM2LSTM’, help=“模型持续更新”)
parser.add_argument(‘-window_size’, type=int, default=64, help=“时间窗口大小, window_size > pre_len”)
parser.add_argument(‘-pre_len’, type=int, default=24, help=“预测未来数据长度”)

#data

​ parser.add_argument(‘-shuffle’, action=‘store_true’, default=True, help=“是否打乱数据加载器中的数据顺序”)
​ parser.add_argument(‘-data_path’, type=str, default=‘ETTh1.csv’, help=“你的数据数据地址”)
​ parser.add_argument(‘-target’, type=str, default=‘OT’, help=‘你需要预测的特征列，这个值会最后保存在csv文件里’)
​ parser.add_argument(‘-input_size’, type=int, default=7, help=‘你的特征个数不算时间那一列’)
​ parser.add_argument(‘-feature’, type=str, default=‘M’, help=‘[M, S, MS],多元预测多元,单元预测单元,多元预测单元’)

parser = argparse.ArgumentParser(description='Time Series forecast')
parser.add_argument('-model', type=str, default='LSTM2LSTM', help="模型持续更新")
parser.add_argument('-window_size', type=int, default=64, help="时间窗口大小, window_size > pre_len")
parser.add_argument('-pre_len', type=int, default=24, help="预测未来数据长度")

# data
parser.add_argument('-shuffle', action='store_true', default=True, help="是否打乱数据加载器中的数据顺序")
parser.add_argument('-data_path', type=str, default='ETTh1.csv', help="你的数据数据地址")
parser.add_argument('-target', type=str, default='OT', help='你需要预测的特征列，这个值会最后保存在csv文件里')
parser.add_argument('-input_size', type=int, default=7, help='你的特征个数不算时间那一列')
parser.add_argument('-feature', type=str, default='M', help='[M, S, MS],多元预测多元,单元预测单元,多元预测单元')
# learning
parser.add_argument('-lr', type=float, default=0.001, help="学习率")
parser.add_argument('-drop_out', type=float, default=0.05, help="随机丢弃概率,防止过拟合")
parser.add_argument('-epochs', type=int, default=20, help="训练轮次")
parser.add_argument('-batch_size', type=int, default=16, help="批次大小")
parser.add_argument('-save_path', type=str, default='models')
 
# model
parser.add_argument('-hidden_size', type=int, default=128, help="隐藏层单元数")
parser.add_argument('-laryer_num', type=int, default=2)
 
# device
parser.add_argument('-use_gpu', type=bool, default=True)
parser.add_argument('-device', type=int, default=0, help="只设置最多支持单个gpu训练")
 
# option
parser.add_argument('-train', type=bool, default=True)
parser.add_argument('-test', type=bool, default=True)
parser.add_argument('-predict', type=bool, default=True)
parser.add_argument('-inspect_fit', type=bool, default=True)
parser.add_argument('-lr-scheduler', type=bool, default=True)
# 可选部分，滚动预测如果想要进行这个需要你有一个额外的文件和你的训练数据集完全相同但是数据时间点不同。
parser.add_argument('-rolling_predict', type=bool, default=True)
parser.add_argument('-roolling_data_path', type=str, default='ETTh1Test.csv', help="你滚动数据集的地址，此部分属于进阶功能")
args = parser.parse_args()

4.结果展示

训练过程损失率

测试过程误差MAE

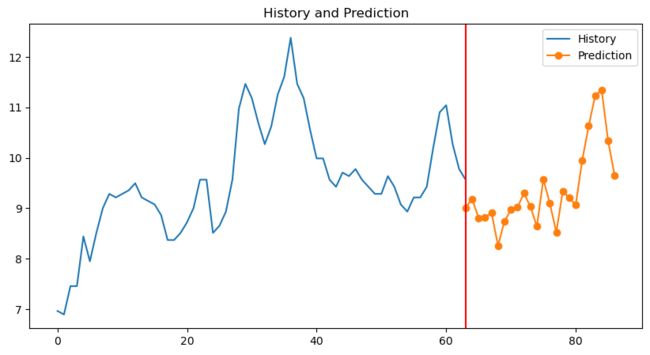
预测结果

5.代码部分

import argparse
import time
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from matplotlib import pyplot as plt
from torch.utils.data import DataLoader
from torch.utils.data import Dataset
from tqdm import tqdm
import torch.nn.functional as F
 
# 随机数种子
np.random.seed(0)
 
 
class StandardScaler():
    def __init__(self):
        self.mean = 0.
        self.std = 1.
 
    def fit(self, data):
        self.mean = data.mean(0)
        self.std = data.std(0)
 
    def transform(self, data):
        mean = torch.from_numpy(self.mean).type_as(data).to(data.device) if torch.is_tensor(data) else self.mean
        std = torch.from_numpy(self.std).type_as(data).to(data.device) if torch.is_tensor(data) else self.std
        return (data - mean) / std
 
    def inverse_transform(self, data):
        mean = torch.from_numpy(self.mean).type_as(data).to(data.device) if torch.is_tensor(data) else self.mean
        std = torch.from_numpy(self.std).type_as(data).to(data.device) if torch.is_tensor(data) else self.std
        if data.shape[-1] != mean.shape[-1]:
            mean = mean[-1:]
            std = std[-1:]
        return (data * std) + mean
 
 
def plot_loss_data(data):
    # 使用Matplotlib绘制线图
    plt.figure()
    plt.figure(figsize=(10, 5))
    plt.plot(data, marker='o')
 
    # 添加标题
    plt.title("loss results Plot")
 
    # 显示图例
    plt.legend(["Loss"])
 
    plt.show()
 
 
class TimeSeriesDataset(Dataset):
    def __init__(self, sequences):
        self.sequences = sequences
 
    def __len__(self):
        return len(self.sequences)
 
    def __getitem__(self, index):
        sequence, label = self.sequences[index]
        return torch.Tensor(sequence), torch.Tensor(label)
 
 
def create_inout_sequences(input_data, tw, pre_len, config):
    # 创建时间序列数据专用的数据分割器
    inout_seq = []
    L = len(input_data)
    for i in range(L - tw):
        train_seq = input_data[i:i + tw]
        if (i + tw + pre_len) > len(input_data):
            break
        if config.feature == 'MS':
            train_label = input_data[:, -1:][i + tw:i + tw + pre_len]
        else:
            train_label = input_data[i + tw:i + tw + pre_len]
        inout_seq.append((train_seq, train_label))
    return inout_seq
 
 
def calculate_mae(y_true, y_pred):
    # 平均绝对误差
    mae = np.mean(np.abs(y_true - y_pred))
    return mae
 
 
def create_dataloader(config, device):
    print(">>>>>>>>>>>>>>>>>>>>>>>>>>>>创建数据加载器<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<")
    df = pd.read_csv(config.data_path)  # 填你自己的数据地址,自动选取你最后一列数据为特征列 # 添加你想要预测的特征列
    pre_len = config.pre_len  # 预测未来数据的长度
    train_window = config.window_size  # 观测窗口
 
    # 将特征列移到末尾
    target_data = df[[config.target]]
    df = df.drop(config.target, axis=1)
    df = pd.concat((df, target_data), axis=1)
 
    cols_data = df.columns[1:]
    df_data = df[cols_data]
 
    # 这里加一些数据的预处理, 最后需要的格式是pd.series
    true_data = df_data.values
 
    # 定义标准化优化器
    scaler = StandardScaler()
    scaler.fit(true_data)
 
    train_data = true_data[int(0.3 * len(true_data)):]
    valid_data = true_data[int(0.15 * len(true_data)):int(0.30 * len(true_data))]
    test_data = true_data[:int(0.15 * len(true_data))]
    print("训练集尺寸:", len(train_data), "测试集尺寸:", len(test_data), "验证集尺寸:", len(valid_data))
 
    # 进行标准化处理
    train_data_normalized = scaler.transform(train_data)
    test_data_normalized = scaler.transform(test_data)
    valid_data_normalized = scaler.transform(valid_data)
 
    # 转化为深度学习模型需要的类型Tensor
    train_data_normalized = torch.FloatTensor(train_data_normalized).to(device)
    test_data_normalized = torch.FloatTensor(test_data_normalized).to(device)
    valid_data_normalized = torch.FloatTensor(valid_data_normalized).to(device)
 
    # 定义训练器的的输入
    train_inout_seq = create_inout_sequences(train_data_normalized, train_window, pre_len, config)
    test_inout_seq = create_inout_sequences(test_data_normalized, train_window, pre_len, config)
    valid_inout_seq = create_inout_sequences(valid_data_normalized, train_window, pre_len, config)
 
    # 创建数据集
    train_dataset = TimeSeriesDataset(train_inout_seq)
    test_dataset = TimeSeriesDataset(test_inout_seq)
    valid_dataset = TimeSeriesDataset(valid_inout_seq)
 
    # 创建 DataLoader
    train_loader = DataLoader(train_dataset, batch_size=args.batch_size, shuffle=True, drop_last=True)
    test_loader = DataLoader(test_dataset, batch_size=args.batch_size, shuffle=False, drop_last=True)
    valid_loader = DataLoader(valid_dataset, batch_size=args.batch_size, shuffle=False, drop_last=True)
 
    print("通过滑动窗口共有训练集数据：", len(train_inout_seq), "转化为批次数据:", len(train_loader))
    print("通过滑动窗口共有测试集数据：", len(test_inout_seq), "转化为批次数据:", len(test_loader))
    print("通过滑动窗口共有验证集数据：", len(valid_inout_seq), "转化为批次数据:", len(valid_loader))
    print(">>>>>>>>>>>>>>>>>>>>>>>>>>>>创建数据加载器完成<<<<<<<<<<<<<<<<<<<<<<<<<<<")
    return train_loader, test_loader, valid_loader, scaler
 
 
class LSTMEncoder(nn.Module):
    def __init__(self, rnn_num_layers=1, input_feature_len=1, sequence_len=168, hidden_size=100, bidirectional=False):
        super().__init__()
        self.sequence_len = sequence_len
        self.hidden_size = hidden_size
        self.input_feature_len = input_feature_len
        self.num_layers = rnn_num_layers
        self.rnn_directions = 2 if bidirectional else 1
        self.lstm = nn.LSTM(
            num_layers=rnn_num_layers,
            input_size=input_feature_len,
            hidden_size=hidden_size,
            batch_first=True,
            bidirectional=bidirectional
        )
 
    def forward(self, input_seq):
 
        ht = torch.zeros(self.num_layers * self.rnn_directions, input_seq.size(0), self.hidden_size, device='cuda')
        ct = ht.clone()
        if input_seq.ndim < 3:
            input_seq.unsqueeze_(2)
        lstm_out, (ht, ct) = self.lstm(input_seq, (ht,ct))
        if self.rnn_directions > 1:
            lstm_out = lstm_out.view(input_seq.size(0), self.sequence_len, self.rnn_directions, self.hidden_size)
            lstm_out = torch.sum(lstm_out, axis=2)
        return lstm_out, ht.squeeze(0)
 
class AttentionDecoderCell(nn.Module):
    def __init__(self, input_feature_len, out_put, sequence_len, hidden_size):
        super().__init__()
        # attention - inputs - (decoder_inputs, prev_hidden)
        self.attention_linear = nn.Linear(hidden_size + input_feature_len, sequence_len)
        # attention_combine - inputs - (decoder_inputs, attention * encoder_outputs)
        self.decoder_rnn_cell = nn.LSTMCell(
            input_size=hidden_size,
            hidden_size=hidden_size,
        )
        self.out = nn.Linear(hidden_size, input_feature_len)
 
    def forward(self, encoder_output, prev_hidden, y):
        if prev_hidden.ndimension() == 3:
            prev_hidden = prev_hidden[-1]  # 保留最后一层的信息
        attention_input = torch.cat((prev_hidden, y), axis=1)
        attention_weights = F.softmax(self.attention_linear(attention_input), dim=-1).unsqueeze(1)
        attention_combine = torch.bmm(attention_weights, encoder_output).squeeze(1)
        rnn_hidden, rnn_hidden = self.decoder_rnn_cell(attention_combine, (prev_hidden, prev_hidden))
        output = self.out(rnn_hidden)
        return output, rnn_hidden
 
 
class EncoderDecoderWrapper(nn.Module):
    def __init__(self, input_size, output_size, hidden_size, num_layers, pred_len, window_size, teacher_forcing=0.3):
        super().__init__()
        self.encoder = LSTMEncoder(num_layers, input_size, window_size, hidden_size)
        self.decoder_cell = AttentionDecoderCell(input_size, output_size,  window_size, hidden_size)
        self.output_size = output_size
        self.input_size = input_size
        self.pred_len = pred_len
        self.teacher_forcing = teacher_forcing
        self.linear = nn.Linear(input_size,output_size)
 
 
    def __call__(self, xb, yb=None):
        input_seq = xb
        encoder_output, encoder_hidden = self.encoder(input_seq)
        prev_hidden = encoder_hidden
        if torch.cuda.is_available():
            outputs = torch.zeros(self.pred_len, input_seq.size(0), self.input_size, device='cuda')
        else:
            outputs = torch.zeros(input_seq.size(0), self.output_size)
        y_prev = input_seq[:, -1, :]
        for i in range(self.pred_len):
            if (yb is not None) and (i > 0) and (torch.rand(1) < self.teacher_forcing):
                y_prev = yb[:, i].unsqueeze(1)
            rnn_output, prev_hidden = self.decoder_cell(encoder_output, prev_hidden, y_prev)
            y_prev = rnn_output
            outputs[i, :, :] = rnn_output
        outputs = outputs.permute(1, 0, 2)
        if self.output_size == 1:
            outputs = self.linear(outputs)
        return outputs
 
 
 
def train(model, args, scaler, device):
    start_time = time.time()  # 计算起始时间
    model = model
    loss_function = nn.MSELoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
    epochs = args.epochs
    model.train()  # 训练模式
    results_loss = []
    for i in tqdm(range(epochs)):
        losss = []
        for seq, labels in train_loader:
            optimizer.zero_grad()
 
            y_pred = model(seq)
 
            single_loss = loss_function(y_pred, labels)
 
            single_loss.backward()
 
            optimizer.step()
            losss.append(single_loss.detach().cpu().numpy())
        tqdm.write(f"\t Epoch {i + 1} / {epochs}, Loss: {sum(losss) / len(losss)}")
        results_loss.append(sum(losss) / len(losss))
 
 
        torch.save(model.state_dict(), 'save_model.pth')
        time.sleep(0.1)
 
    # valid_loss = valid(model, args, scaler, valid_loader)
    # 尚未引入学习率计划后期补上
    # 保存模型
 
    print(f">>>>>>>>>>>>>>>>>>>>>>模型已保存,用时:{(time.time() - start_time) / 60:.4f} min<<<<<<<<<<<<<<<<<<")
    plot_loss_data(results_loss)
 
 
def valid(model, args, scaler, valid_loader):
    lstm_model = model
    # 加载模型进行预测
    lstm_model.load_state_dict(torch.load('save_model.pth'))
    lstm_model.eval()  # 评估模式
    losss = []
 
    for seq, labels in valid_loader:
        pred = lstm_model(seq)
        mae = calculate_mae(pred.detach().numpy().cpu(), np.array(labels.detach().cpu()))  # MAE误差计算绝对值(预测值  - 真实值)
        losss.append(mae)
 
    print("验证集误差MAE:", losss)
    return sum(losss) / len(losss)
 
 
def test(model, args, test_loader, scaler):
    # 加载模型进行预测
    losss = []
    model = model
    model.load_state_dict(torch.load('save_model.pth'))
    model.eval()  # 评估模式
    results = []
    labels = []
    for seq, label in test_loader:
        pred = model(seq)
        mae = calculate_mae(pred.detach().cpu().numpy(),
                            np.array(label.detach().cpu()))  # MAE误差计算绝对值(预测值  - 真实值)
        losss.append(mae)
        pred = pred[:, 0, :]
        label = label[:, 0, :]
        pred = scaler.inverse_transform(pred.detach().cpu().numpy())
        label = scaler.inverse_transform(label.detach().cpu().numpy())
        for i in range(len(pred)):
            results.append(pred[i][-1])
            labels.append(label[i][-1])
    plt.figure(figsize=(10, 5))
    print("测试集误差MAE:", losss)
    # 绘制历史数据
    plt.plot(labels, label='TrueValue')
 
    # 绘制预测数据
    # 注意这里预测数据的起始x坐标是历史数据的最后一个点的x坐标
    plt.plot(results, label='Prediction')
 
    # 添加标题和图例
    plt.title("test state")
    plt.legend()
    plt.show()
 
 
# 检验模型拟合情况
def inspect_model_fit(model, args, train_loader, scaler):
    model = model
    model.load_state_dict(torch.load('save_model.pth'))
    model.eval()  # 评估模式
    results = []
    labels = []
 
    for seq, label in train_loader:
        pred = model(seq)[:, 0, :]
        label = label[:, 0, :]
        pred = scaler.inverse_transform(pred.detach().cpu().numpy())
        label = scaler.inverse_transform(label.detach().cpu().numpy())
        for i in range(len(pred)):
            results.append(pred[i][-1])
            labels.append(label[i][-1])
    plt.figure(figsize=(10, 5))
    # 绘制历史数据
    plt.plot(labels, label='History')
 
    # 绘制预测数据
    # 注意这里预测数据的起始x坐标是历史数据的最后一个点的x坐标
    plt.plot(results, label='Prediction')
 
    # 添加标题和图例
    plt.title("inspect model fit state")
    plt.legend()
    plt.show()
 
 
def predict(model=None, args=None, device=None, scaler=None, rolling_data=None, show=False):
    # 预测未知数据的功能
    df = pd.read_csv(args.data_path)
    df = pd.concat((df,rolling_data), axis=0).reset_index(drop=True)
    df = df.iloc[:, 1:][-args.window_size:].values  # 转换为nadarry
    pre_data = scaler.transform(df)
    tensor_pred = torch.FloatTensor(pre_data).to(device)
    tensor_pred = tensor_pred.unsqueeze(0)  # 单次预测 , 滚动预测功能暂未开发后期补上
    model = model
    model.load_state_dict(torch.load('save_model.pth'))
    model.eval()  # 评估模式
 
    pred = model(tensor_pred)[0]
 
    pred = scaler.inverse_transform(pred.detach().cpu().numpy())
    if show:
        # 计算历史数据的长度
        history_length = len(df[:, -1])
        # 为历史数据生成x轴坐标
        history_x = range(history_length)
        plt.figure(figsize=(10, 5))
        # 为预测数据生成x轴坐标
        # 开始于历史数据的最后一个点的x坐标
        prediction_x = range(history_length - 1, history_length + len(pred[:, -1]) - 1)
 
        # 绘制历史数据
        plt.plot(history_x, df[:, -1], label='History')
 
        # 绘制预测数据
        # 注意这里预测数据的起始x坐标是历史数据的最后一个点的x坐标
        plt.plot(prediction_x, pred[:, -1], marker='o', label='Prediction')
        plt.axvline(history_length - 1, color='red')  # 在图像的x位置处画一条红色竖线
        # 添加标题和图例
        plt.title("History and Prediction")
        plt.legend()
    return pred
 
def rolling_predict(model=None, args=None, device=None, scaler=None):
    # 滚动预测
    history_data = pd.read_csv(args.data_path)[args.target][-args.window_size * 4:].reset_index(drop=True)
    pre_data = pd.read_csv(args.roolling_data_path)
    columns = pre_data.columns[1:]
    columns = ['forecast' + column for column in columns]
    dict_of_lists = {column: [] for column in columns}
    results = []
    for i in range(int(len(pre_data)/args.pre_len)):
        rolling_data = pre_data.iloc[:args.pre_len * i]  # 转换为nadarry
        pred = predict(model, args, device, scaler, rolling_data)
        if args.feature == 'MS' or args.feature == 'S':
            for i in range(args.pred_len):
                results.append(pred[i][0].detach().cpu().numpy())
        else:
            for j in range(args.output_size):
                for i in range(args.pre_len):
                    dict_of_lists[columns[j]].append(pred[i][j])
        print(pred)
    if args.feature == 'MS' or args.feature == 'S':
          df = pd.DataFrame({'date':pre_data['date'], '{}'.format(args.target): pre_data[args.target],
                             'forecast{}'.format(args.target): pre_data[args.target]})
          df.to_csv('Interval-{}'.format(args.data_path), index=False)
    else:
        df = pd.DataFrame(dict_of_lists)
        new_df = pd.concat((pre_data,df), axis=1)
        new_df.to_csv('Interval-{}'.format(args.data_path), index=False)
    pre_len = len(dict_of_lists['forecast' + args.target])
    # 绘图
    plt.figure()
    if args.feature == 'MS' or args.feature == 'S':
        plt.plot(range(len(history_data)), history_data,
                 label='Past Actual Values')
        plt.plot(range(len(history_data), len(history_data) + pre_len), pre_data[args.target][:pre_len].tolist(), label='Predicted Actual Values')
        plt.plot(range(len(history_data), len(history_data) + pre_len), results, label='Predicted Future Values')
    else:
        plt.plot(range(len(history_data)), history_data,
                 label='Past Actual Values')
        plt.plot(range(len(history_data), len(history_data) + pre_len), pre_data[args.target][:pre_len].tolist(), label='Predicted Actual Values')
        plt.plot(range(len(history_data), len(history_data) + pre_len), dict_of_lists['forecast' + args.target], label='Predicted Future Values')
    # 添加图例
    plt.legend()
    plt.style.use('ggplot')
    # 添加标题和轴标签
    plt.title('Past vs Predicted Future Values')
    plt.xlabel('Time Point')
    plt.ylabel('Value')
    # 在特定索引位置画一条直线
    plt.axvline(x=len(history_data), color='blue', linestyle='--', linewidth=2)
    # 显示图表
    plt.savefig('forcast.png')
    plt.show()
 
 
 
if __name__ == '__main__':
    parser = argparse.ArgumentParser(description='Time Series forecast')
    parser.add_argument('-model', type=str, default='LSTM2LSTM', help="模型持续更新")
    parser.add_argument('-window_size', type=int, default=64, help="时间窗口大小, window_size > pre_len")
    parser.add_argument('-pre_len', type=int, default=24, help="预测未来数据长度")
    # data
    parser.add_argument('-shuffle', action='store_true', default=True, help="是否打乱数据加载器中的数据顺序")
    parser.add_argument('-data_path', type=str, default='ETTh1.csv', help="你的数据数据地址")
    parser.add_argument('-target', type=str, default='OT', help='你需要预测的特征列，这个值会最后保存在csv文件里')
    parser.add_argument('-input_size', type=int, default=7, help='你的特征个数不算时间那一列')
    parser.add_argument('-feature', type=str, default='M', help='[M, S, MS],多元预测多元,单元预测单元,多元预测单元')
 
    # learning
    parser.add_argument('-lr', type=float, default=0.001, help="学习率")
    parser.add_argument('-drop_out', type=float, default=0.05, help="随机丢弃概率,防止过拟合")
    parser.add_argument('-epochs', type=int, default=20, help="训练轮次")
    parser.add_argument('-batch_size', type=int, default=16, help="批次大小")
    parser.add_argument('-save_path', type=str, default='models')
 
    # model
    parser.add_argument('-hidden_size', type=int, default=128, help="隐藏层单元数")
    parser.add_argument('-laryer_num', type=int, default=2)
 
    # device
    parser.add_argument('-use_gpu', type=bool, default=True)
    parser.add_argument('-device', type=int, default=0, help="只设置最多支持单个gpu训练")
 
    # option
    parser.add_argument('-train', type=bool, default=True)
    parser.add_argument('-test', type=bool, default=True)
    parser.add_argument('-predict', type=bool, default=True)
    parser.add_argument('-inspect_fit', type=bool, default=True)
    parser.add_argument('-lr-scheduler', type=bool, default=True)
    # 可选部分，滚动预测如果想要进行这个需要你有一个额外的文件和你的训练数据集完全相同但是数据时间点不同。
    parser.add_argument('-rolling_predict', type=bool, default=True)
    parser.add_argument('-roolling_data_path', type=str, default='ETTh1Test.csv', help="你滚动数据集的地址，此部分属于进阶功能")
    args = parser.parse_args()
 
    if isinstance(args.device, int) and args.use_gpu:
        device = torch.device("cuda:" + f'{args.device}')
    else:
        device = torch.device("cpu")
    print("使用设备:", device)
    train_loader, test_loader, valid_loader, scaler = create_dataloader(args, device)
 
    if args.feature == 'MS' or args.feature == 'S':
        args.output_size = 1
    else:
        args.output_size = args.input_size
 
    # 实例化模型
    try:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始初始化{args.model}模型<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        model = EncoderDecoderWrapper(args.input_size, args.output_size, args.hidden_size, args.laryer_num, args.pre_len, args.window_size).to(device)
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始初始化{args.model}模型成功<<<<<<<<<<<<<<<<<<<<<<<<<<<")
    except:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始初始化{args.model}模型失败<<<<<<<<<<<<<<<<<<<<<<<<<<<")
 
    # 训练模型
    if args.train:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始{args.model}模型训练<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        train(model, args, scaler, device)
    if args.test:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始{args.model}模型测试<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        test(model, args, test_loader, scaler)
    if args.inspect_fit:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始检验{args.model}模型拟合情况<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        inspect_model_fit(model, args, train_loader, scaler)
    if args.predict:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>预测未来{args.pre_len}条数据<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        predict(model, args, device, scaler,show=True)
    if args.predict:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>滚动预测未来{args.pre_len}条数据<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        rolling_predict(model, args, device, scaler)
    plt.show()

小结

本周主要学习了流模型。首先了解了之前学习模型的缺点，其次学习了相关的数学知识，即雅可比矩阵、行列式、change of variable theorem。之后开始介绍流模型。

• 根据GAN的主要框架阐述了流模型的设计思路，
• 介绍了流模型的训练过程，
• 介绍了coupling layer的内部构造，
  • 假设总计D维数据，该模型复制前d维数据并通过F、H两个映射将前d维数据映射为D-d维向量，经过处理后使用这些向量得到D-d维数据。
  • 解释了该算法如何降低雅可比行列式的计算难度
  • coupling layer首尾相连构造模型时，会因为单一的固定前d维数据导致其不会发生变换，因此描述了如何通过变换固定的维度来达到使得各维数据均能得到充分的变换
• 介绍了GLOW模型
  • 该模型收到了流模型的启发，将其设计为1*1卷积层

Density estimation using Real NVP的主要内容概述：

• change of variable formula
  • 设计一个双射，并按照（2）（3）进行变换，相应的推导出反变换过程用于数据的生成。
• coupling layer
  • 为了降低雅可比矩阵的计算成本，该文设计了仿射耦合层，建立一个灵活且易于处理的双射函数并将其叠加为一个复杂的双射，该双射以复杂的方式依赖于输入向量的其余分布，且其反变换较为简单。
• properties：阐述网络的大致结构
• masked convolution
  • 即上文中提到的变换固定的维度以达到使得各维数据均能得到充分的处理。

下周计划学习自监督学习以及BERT，阅读提出GLOW的论文。

参考文献

[1]Dinh, Laurent, et al. “Density Estimation Using Real NVP.” arXiv.Org, 27 Feb. 2017, arxiv.org/abs/1605.08803.

[2] Karen Simonyan and Andrew Zisserman. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.

[3]Aaron van den Oord, Nal Kalchbrenner, and Koray Kavukcuoglu. Pixel recurrent neural networks. arXiv preprint arXiv:1601.06759, 2016.