D47|动态规划-子序列part2
392.判断子序列:
初始思路:
左为判断公共子序列,右为判断子序列,感觉代码完全可以套用,如果公共子序列的长度是较短的字符串的长度的话即输出true,如果不是即输出false。
class Solution {
public boolean isSubsequence(String s, String t) {
if(s.length()==0&&t.length()==0){return true;}
if(t.length()==0){return false;}
char[] sc = s.toCharArray();
char[] tc = t.toCharArray();
int length = sc.length题解复盘:
完全不一样的思路,一个新的操纵方法:编辑距离!
动态规划五部曲:
1)确定dp数组(dp table)以及下标的含义:
dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]
2)确定递推公式:
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在dp[i-1][j-1]的基础上加1(如果不理解,在回看一下dp[i][j]的定义)
if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1]
class Solution {
public boolean isSubsequence(String s, String t) {
int length1 = s.length(); int length2 = t.length();
int[][] dp = new int[length1+1][length2+1];
for(int i = 1; i <= length1; i++){
for(int j = 1; j <= length2; j++){
if(s.charAt(i-1) == t.charAt(j-1)){
dp[i][j] = dp[i-1][j-1] + 1;
}else{
dp[i][j] = dp[i][j-1];
}
}
}
if(dp[length1][length2] == length1){
return true;
}else{
return false;
}
}
}115.不同的子序列:
初始思路&&题解复盘:
动态规划五部曲;
1)dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
2)确定递推公式:
- s[i - 1] 与 t[j - 1]相等
- s[i - 1] 与 t[j - 1] 不相等
当s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。
1)一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母,所以只需要 dp[i-1][j-1]。
2)一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
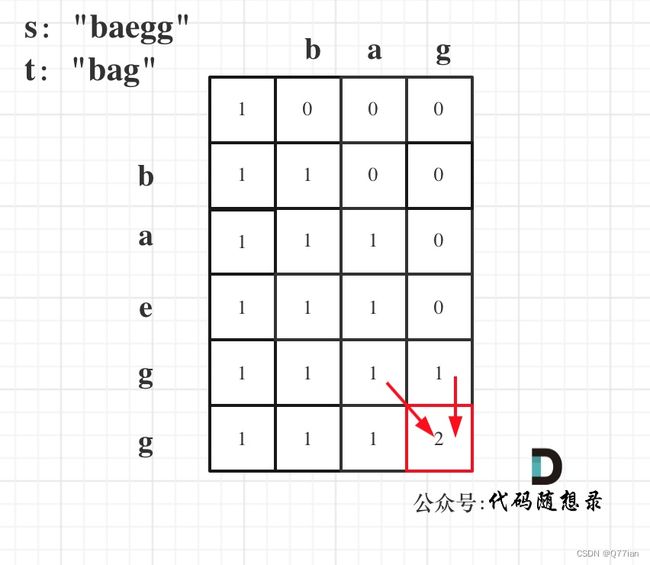
例如: s:baegg 和 t:bag ,s[4] 和 t[2]是相同的,但是字符串s也可以不用s43]来匹配,即用s[0]s[1]s[3]组成的bag。
当然也可以用s[4]来匹配,即:s[0]s[1]s[4]组成的bag。
当s[i - 1] 与 t[j - 1]不相等时,dp[i][j]只有一部分组成,不用s[i - 1]来匹配(就是模拟在s中删除这个元素),即:dp[i - 1][j]
所以递推公式为:dp[i][j] = dp[i - 1][j]
3)初始化:
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来,如图:,那么 dp[i][0] 和dp[0][j]是一定要初始化的。
每次当初始化的时候,都要回顾一下dp[i][j]的定义,不要凭感觉初始化。
dp[i][0]表示什么呢?
dp[i][0] 表示:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。
那么dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1。
再来看dp[0][j],dp[0][j]:空字符串s可以随便删除元素,出现以j-1为结尾的字符串t的个数(它都一直是空字符串了,那怎么能有元素咧!)。
那么dp[0][j]一定都是0,s如论如何也变成不了t。
最后就要看一个特殊位置了,即:dp[0][0] 应该是多少。
dp[0][0]应该是1,空字符串s,可以删除0个元素,变成空字符串t。
4)遍历顺序
5)举例:
class Solution {
public int numDistinct(String s, String t) {
char[] sc = s.toCharArray();
char[] st = t.toCharArray();
int[][] dp = new int[sc.length+1][st.length+1];
for(int i = 0;i