论文阅读：A Rotation-Translation-Decoupled Solution for Robust and Efficient VI Initialization

前言

这是一篇发表在CVPR2023上的文章，A Rotation-Translation-Decoupled Solution for Robust and Efficient Visual-Inertial Initialization，深蓝学院还有作者对这项工作的介绍：

VIO 初始化探究：旋转平移解耦的高效鲁棒初始化 - 深蓝学院 - 专注人工智能与自动驾驶的学习平台https://www.shenlanxueyuan.com/open/course/185/lesson/169/liveToVideoPreview这篇文章的主要工作，是提出了一种新的视觉-惯性里程计( VIO )初始化方法，该方法将旋转和平移估计解耦，具有更高的效率和更好的鲁棒性。并开源了代码：

http://https: //github.com/boxuLibrary/drt-vio-init

一、问题背景

初始值的精度会影响收敛，初始化的鲁棒性和较低的延迟对于下游应用也是非常重要的。对于标定了内外参数的传感器，VIO的初始变量包括重力矢量、初始速度、陀螺仪和加速度计零偏。

对于松耦合初始化方法：当共视帧数不足或相机快速旋转时，视觉SfM容易出现不准确或失效的情况。没有利用IMU测量的运动信息来提高视觉SfM的鲁棒性。

对于紧耦合初始化方法：在搭载价格低廉且带有噪声的IMU (例如,手机)的系统上精度较差，因为没有使用视觉观测来估计陀螺仪偏差。此外，点云的三维坐标是通过闭式求解得到的，导致求解矩阵庞大且耗时。

上述两种方法均未充分利用视觉和惯性传感器之间的优势互补，导致精度和鲁棒性受限。

二、理论流程

由于旋转会影响平移向量的积累，因此准确、鲁棒的旋转估计对于提高系统的轨迹精度至关重要。在这一部分中，我们首先介绍了我们使用至少两幅图像对陀螺仪偏差进行鲁棒估计的方法。然后，我们推导了通过陀螺仪积分得到旋转后的初始速度和重力矢量的两个线性解。

1、陀螺仪零偏优化器

两个相机之间的旋转可以直接利用特征对应关系构造的几何约束进行迭代优化[ 17 ]，但该方法要求旋转的初始值接近真实值。我们将该方法扩展到视觉-惯性系以避免上述问题，并将其扩展到解决多视图之间的旋转。

假设我们在两个框架中观察到n个3D点，将所有的法向量堆叠成一个矩阵N = [ n1 ... nn]，则共面性在代数上等价于矩阵M = NN的最小特征值等于零。计算相对旋转Rcicj的最终问题被参数化为

结合式( 1 ) ( 3 )、( 4 )和( 5 )中，Mij可以表示为一个新的与陀螺仪信息相关的矩阵

利用旋转矩阵和向量叉积的性质，Eq . ( 6 )可以进一步简化为如下形式

为了充分利用所有的视觉观测，将多个关键帧对组合在一起以优化解决方案

2、速度和重力估值器

在计算出旋转后，无需估计三维点云，就可以高效地求解出系统的初始速度和重力矢量。在这一部分中，分别提出了基于线性平移约束的紧耦合和松耦合求解器。

（1）紧耦合求解

假设多帧序列的第一帧为世界坐标系，直接利用线性全局平移约束[ 3 ]，可以高效地求解出每一帧在世界坐标系中的位置。假设有三个关键帧，并且这些关键帧的索引分别为r，i和l。LiGT约束可表示为

当我们有三个以上关键帧，有多个B、C、D，可以连接它们并定义为只包含视觉观测和全局旋转的系数矩阵L。

所有摄像机关于第一个关键帧的位置可以通过等式求解。( 11 )。由于式( 1 )的平移向量为式( 9 )都是关于相机坐标系的，代入式( 10 )得( 5 )代入Eq . ( 9 )将相机坐标系转换为IMU坐标系。

上述公式中的所有全局平移量都可以用式( 1 )中的IMU积分公式代替。( 1 ) .因此，求解全局位置的线性方程组( 11 )转化为求解初始速度和重力矢量的方程组：

（2）松耦合求解

松耦合方法需要首先计算相机平移，然后结合IMU测量值计算初始状态变量。相机位姿可由式( 1 )计算得到( 9 )。如果使用单目相机，由LiGT约束得到的位置是尺度的，那么在初始化时需要显式地计算尺度因子s。定义X为初始状态变量的向量，vbn bn为物体在Fbn中的速度，gc0为物体在Fc0中的重力，s为度规。

假设两个关键帧对应的身体坐标系为Fbi和Fbk，IMU和视觉测量之间存在如下约束[ 31 ]

残差是估计值和测量值之间的差值，它可以参数化为

在有噪声的情况下这个系统没有精确解，所以我们仍然使用最小二乘解。

最后，我们将多个相邻帧生成的H′堆叠成一个系数矩阵H，对于b′和b也是如此。求解最小二乘解HX = b，X即可得到。对于H′和b′的具体形式，请参考补充材料Sec.2。

三、实验方案

做了仿真实验与真实场景实验。

1、仿真实验

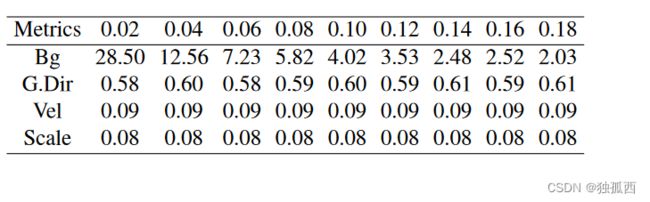
仿真结果表明，我们的方法不仅可以在不同的陀螺仪偏置幅度上收敛，而且可以准确地初始化状态变量。

2、真实实验

准确性评估

鲁棒性评估

耗时评估

四、创新总结

陀螺仪测量值直接融入相机旋转估计，大大提高了初始化的鲁棒性，在不估计三维结构的情况下高效求解平移相关的初始变量。

提出了一种仅使用图像观测直接优化陀螺仪偏置的旋转解决方案，与仅使用视觉的方法相比，可以更有效和更鲁棒地获得相机旋转。

提出了一种基于线性平移约束的估计初始速度和重力矢量的全局最优解决方案。

提出的初始化框架在公共数据集上的准确性和鲁棒性都优于最先进的方法，同时在10帧数据集上的计算时间比最先进的方法快8-72倍。

之前听那个讲座的时候还懂一点，现在感觉论文看不太懂...但这篇论文开源了代码并且有视频讲解，将来如果在实际中应用还是很不错的。