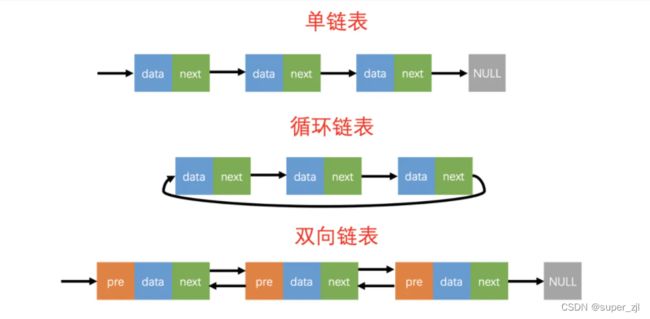
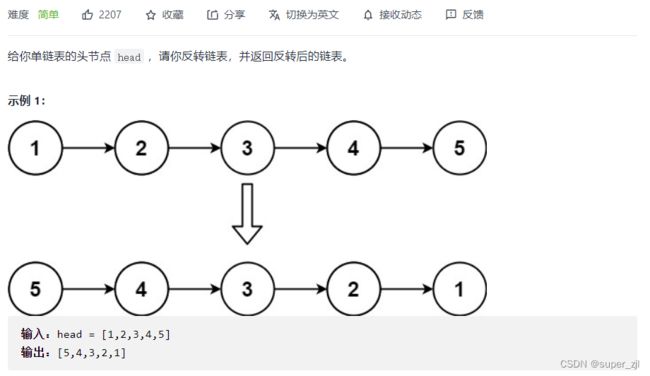
现在还不懂什么是链表?
一、什么是链表
链表和数组一样,也是一种线性表。只不过不同于数组,从内存结构来看,链表的内存结构是不连续的内存空间,是将一组零散的内存块串联起来,从而进行数据存储的数据结构。
链表中的每一个内存块被称为节点Node。节点除了存储数据外,还需记录链上下一个节点的地址,即后继指针next,在特殊的链表结构中,甚至还需要保留上一个节点的地址,即前驱指针。
二、链表和数组的区别
比如说:Java中
ArrayList和LinkedList的之间区别?
-
数组的随机访问快,插入和删除慢
-
链表的插入删除快,随机访问慢
-
频繁增删的情况下,用链表比较合适
-
在随机查找多的情况下,用数组比较合适
因为数组是连续存储的,支持随机访问,所以根据首地址和下标,通过寻址公式就能直接计算出对应的内存地址,时间复杂度为 O(1)。
三、常用链表
3.1 单链表
3.1.1 单链表特点
单链表作为最常见的链表结构,如图所示:
-
单链表的每个节点包含下一个节点的地址指针,即后继指针;
-
头结点,即链表的第一个结点,用来记录链表的基地址,我们只要知道这个结点,就可以开始遍历整条链表;
-
尾结点,即最后一个结点,因此尾结点后继指针next指向的不再是下一个节点。而是指向一个空地址null。
3.1.2 为什么单链表的尾结点指向一个空地址
单链表的尾结点指向空地址的好处是:防止尾节点的后继指针next成为一个野指针,导致遍历链表根本停不下来,或者出现一堆本不属于该链表的垃圾数据;
3.1.3 单链表操作复杂度分析
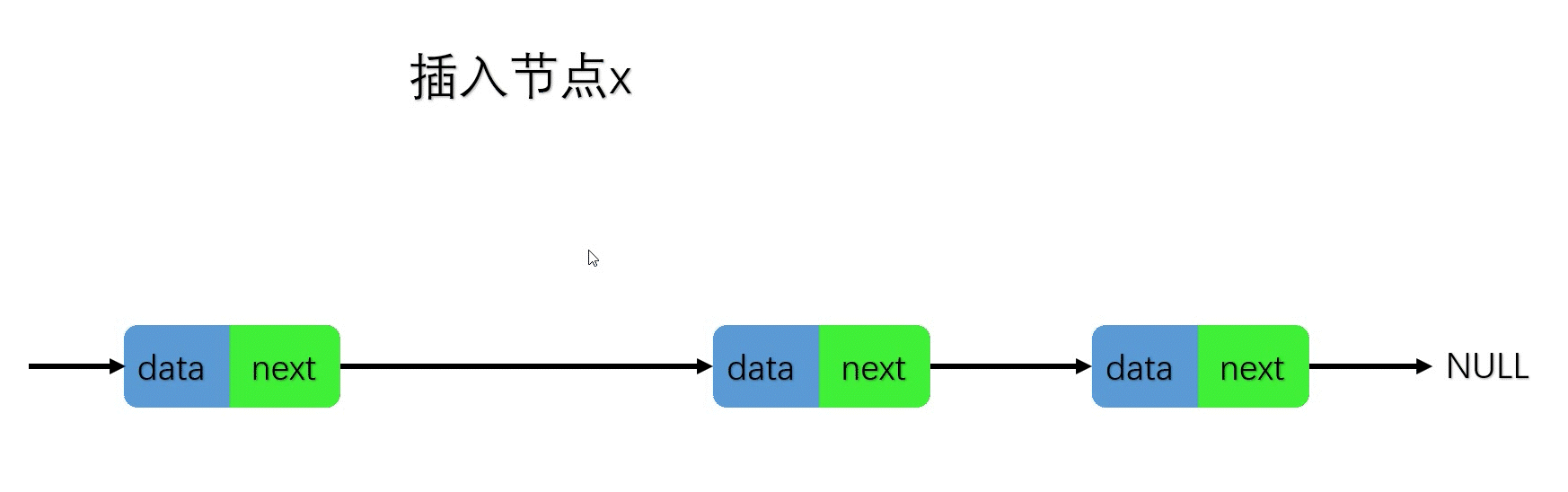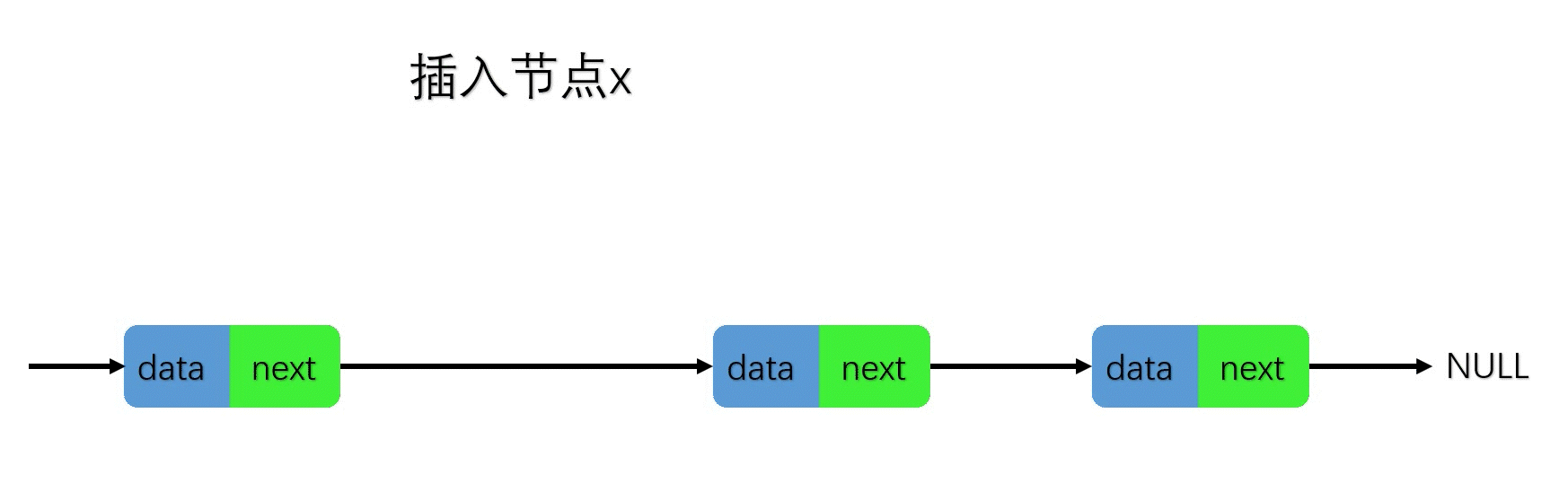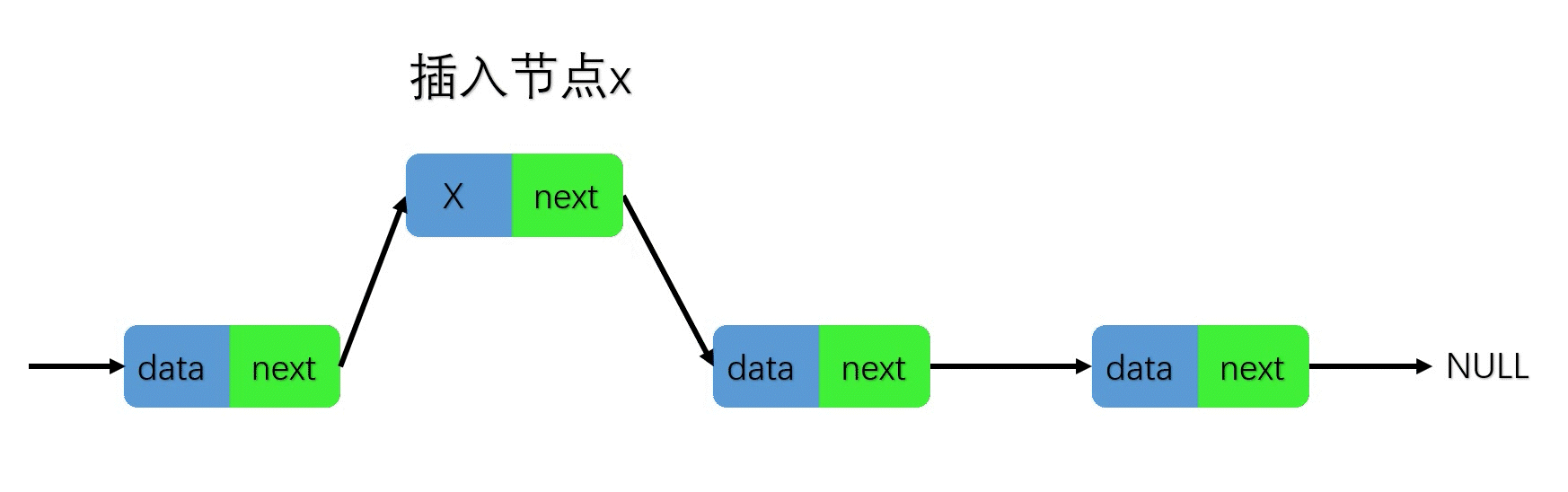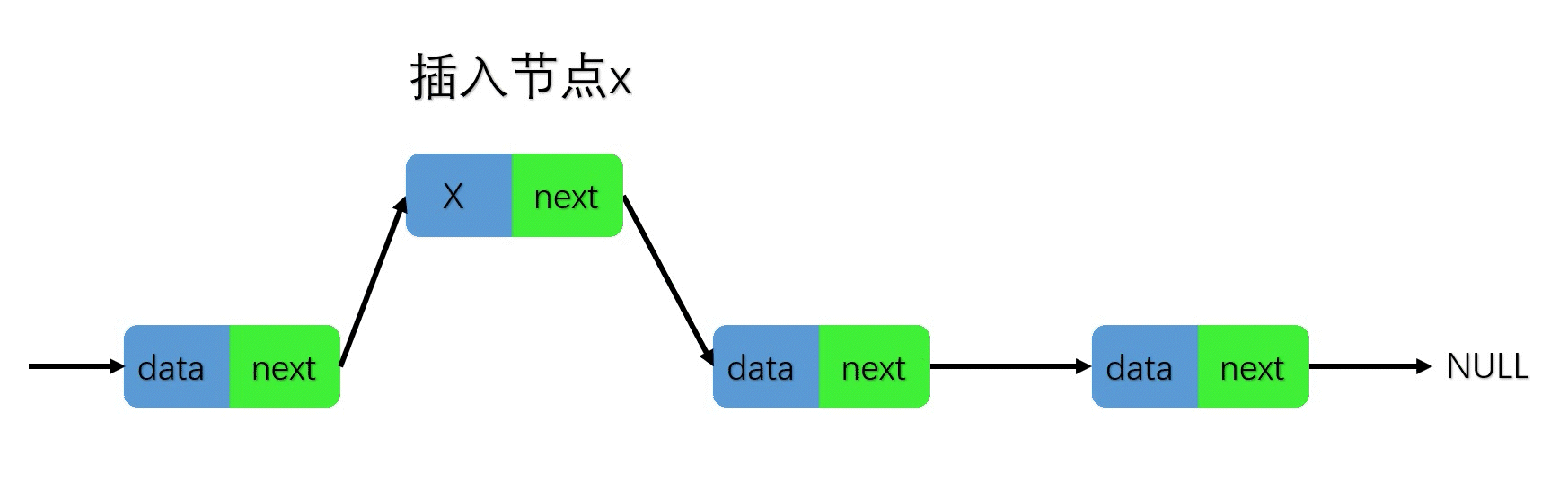
插入时,只需要更改指针指向的对象地址即可,无需迁移数据,因此链表的插入和删除操作时间复杂度为O(1)。找到前驱节点的时间复杂度为O(n),所以总时间复杂度为O(1)+O(n)=O(n)。
如果是要在链表中实现随机访问或者是根据下标访问,那么需要根据头结点进行遍历查询,时间复杂度为O(n)。
3.2 循环链表
循环链表和单链表非常类似,唯一区别在于:循环列表的尾节点后继指针指向首节点的地址,因此又称为单循环列表。
-
循环链表是无须增加存储量,仅对表的链接方式稍作改变,即可使得表处理更加方便灵活。
-
循环链表中没有NULL指针。涉及遍历操作时,其终止条件就不再是像非循环链表那样判别p或p->next是否为空,而是判别它们是否等于某一指定指针,如头指针或尾指针等。
-
在单链表中,从一已知结点出发,只能访问到该结点及其后续结点,无法找到该结点之前的其它结点。而在单循环链表中,从任一结点出发都可访问到表中所有结点,这一优点使某些运算在单循环链表上易于实现。
但是在实际应用中,循环列表好像只适用于简单的循环列表类型的问题处理。
3.3 双向链表
双向链表的结点除了存储数据和后继指针next之外,还会存储前一个结点的地址,即前驱指针pre,用来向前查询当然,尾结点的后继指针依旧指向一个空地址,头结点的前驱指针也是如此。
和单链表相比,存储相同的数据,由于需要存放两个指针数据,需要消耗更多的存储空间。
双向链表在各种操作时的复杂度分析会是什么样的呢?
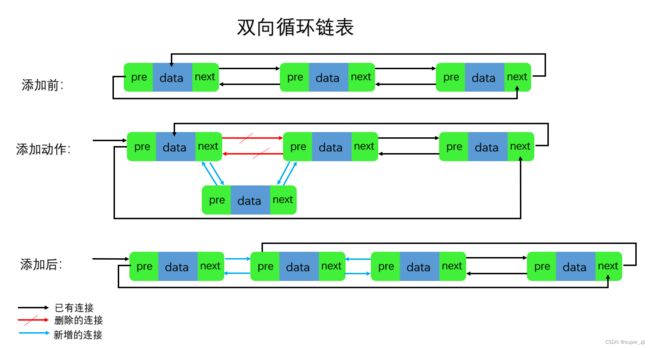
3.3.1 插入操作
双向链表的插入操作也是O(1)级别,好像在效率上没有提升,甚至好像还有些降低,因为单链表只需要修改后继结点,双向链表需要修改前驱结点和后继结点的值。但是如果是删除操作,那么复杂度的提升还是比较明显;
3.3.2 删除操作
删除操作分为2种情况:给定数据值删除对应节点和给定节点地址删除节点。
对于给定数据值删除对应节点,单链表和双向链表都需要从头到尾进行遍历从而找到对应节点进行删除,时间复杂度为O(n)。
删除给定指针指向的结点:这种情况是已经找到了要删除的元素,我们只需要执行删除操作即可.
对比分析:
-
针对单链表而言:单链表如果要删除一个结点q.必须要知道这个结点的前驱结点是谁,修改前驱结点的指针指向即可.单链表找某个结点的前驱结点,只能从头开始遍历. 临界值 p->next == q;说明p就是q的前驱结点.所以在单链表中,找这个前驱结点的平均时间复杂度为O(n),然后执行删除操作的时间复杂度为O(1). 根据时间复杂度分析的加法法则: 删除给定指针指向的结点 --> 单链表的总的时间复杂度为O(n).
-
针对双链表而言: 双链表要删除一个结点q.也必须得知道这个结点的前驱结点和后继结点. 修改前驱结点的后继指针next和后继结点的前驱指针prev即可.而针对双链表而言,找q的前驱结点和q的后继结点的时间复杂度都为O(1).而执行删除操作(修改指针指向)的时间复杂度也为O(1). 根据时间复杂度分析的加法法则: 删除给定指针指向的结点 --> 双链表的总的时间复杂度为O(1).
至于查找,的时间复杂度均为O(n)。 对于最基本的CRUD操作,双链表优势在于删除给定节点。但其劣势在于浪费存储空间(若从工程角度考量,则其维护性和可读性都更低)。
3.3.3 查找操作
无序链表,那么查询元素都需要从头结点进行遍历查询,双向链表并没有什么优势。
有序链表,双向链表的按值查询效率要比单链表高一些。因为我们可以记录上次查找的位置p,每一次查询时,根据要查找的值与p的大小关系,决定是往前还是往后查找,所以平均只需要查找一半的数据。
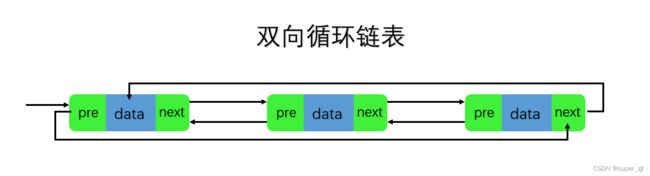
3.4 双向循环链表
了解了上面的循环链表以及双向链表,两者结合就是双向循环链表,即:首节点的前驱指针指向尾节点,尾节点的后继指针指向首节点,如图所示。
单链表的缺点是只能往前,不能后退,虽然有循环单链表,但后退的成本还是很高的,需要跑一圈。在这个时候呢,双向链表就应运而生了,再加上循环即双向循环链表就更加不错了。所谓双向链表只不过是添加了一个指向前驱结点的指针,而双向循环链表是将最后一个结点的后继指针指向头结点。
四、使用链表的目的?
“链表是为了解决什么问题而出现的”、
“有没有更优方案”、“如何找出更优方案”、
“如何证明方案更优”……从而
“当我遇到某个难题时,该如何优雅的解决它?”
3.1 为了解决什么问题而出现的?
为了解决动态数量的数据存储。
举个例子:我们要管理一堆票据,可能有一张,但也可能有一亿张。
怎么办呢?申请50G的大数组等着?万一用户只有一百张票据要处理呢?万一申请少了又不够用呢?
用数组的话,删除然后添加票据,是每次删除让后面五百万张往前移一格呢等等,有太多问题。
那么,此时链表就是个很有效的数据结构,可以很有效的管理这类不定量的数据。
3.2 有没有更优方案?
-
时间上:链表无法支持搜索,想找到特定数据只能遍历。
-
空间上:链表每个数据要额外占用一个指针的空间;对于int等基本数据类型,数据量暴增一倍(单链表)甚至两倍。
所以,为了在时间上优化它,可以搞成二叉树;然后通过先序/后序/中序遍历取得按一定规律排布的数据;也可以通过和根节点比较来快速确定数据在排序二叉树的左还是右子树上——这就得到了O(logN)的时间复杂度的查询效率。那么二叉树的查询效率怎样才能更高,性能更稳定,于是就有了满二叉树、平衡树、红黑树等概念/算法。
堆是一种优化到极致的二叉树;它实际上就是一个数组,左右节点对应的数组下标可以直接计算出来——这就省掉了指向子节点的指针。
五、链表的面试算法题
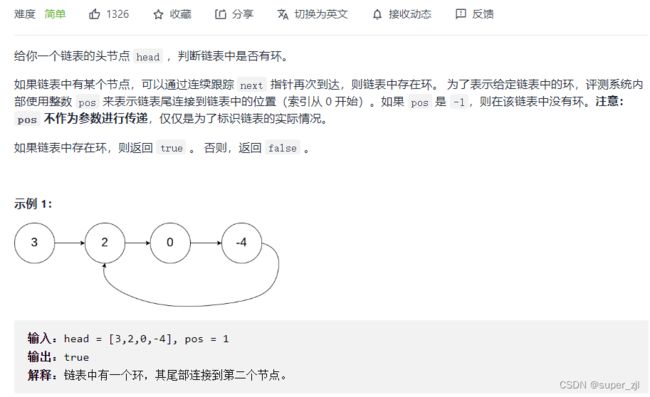
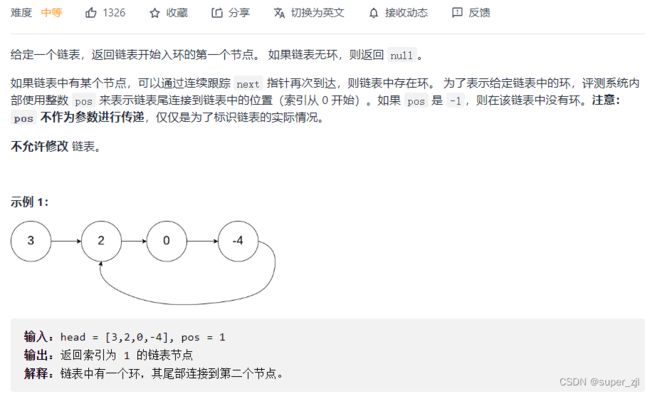
1.环形链表
题目
思路一:哈希表法
-
HashSet的底层是HashMap实现
/**
* 思路一:哈希表
* @param head
* @return
*/
public boolean hasCycle(ListNode head) {
//创建hashSet
HashSet hashSet = new HashSet();
while (head != null) {
//hashSet.add(head) 如果里面没有该节点返回true,并且将head节点添加到hashSet里面
//如果里面有该节点返回false
if (!hashSet.add(head)) {
return true;
}
head = head.next;
}
return false;
}
public class ListNode {
int val;
ListNode next;
ListNode() {
}
ListNode(int val) {
this.val = val;
}
ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
} 思路二:快慢指针
/**
* 思路二:快慢指针
* @param head
* @return
*/
public boolean hasCycle2(ListNode head) {
if(head == null) return false;
//创建快慢指针,同时指向head
ListNode fast = head,slow = head;
//使用do while处理特殊情况:指针从头开始
do{
//无环情况:快指针或快指针的下一个指针域指向null
if(fast == null || fast.next == null){
return false;
}
slow = slow.next;
fast = fast.next.next;
}while(fast != slow);
//有环情况:fast=slow,且没有返回false
return true;
}
//默认链表结构体
public class ListNode {
int val;
ListNode next;
ListNode() {
}
ListNode(int val) {
this.val = val;
}
ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
}2.环形链表 II
题目
思路一:哈希表法
/**
* 思路一:哈希表
* @param head
* @return
*/
public ListNode detectCycle(ListNode head) {
//创建hashSet
HashSet hashset = new HashSet();
while(head != null){
//有环情况:当存入重复值代表有环,add返回false,进入if循环,返回head。
if(!hashset.add(head)){
return head;
}
head = head.next;
}
//无环情况:在哈希表里存的所有值都没有重复,则表示无环
return null;
} 思路二:快慢指针
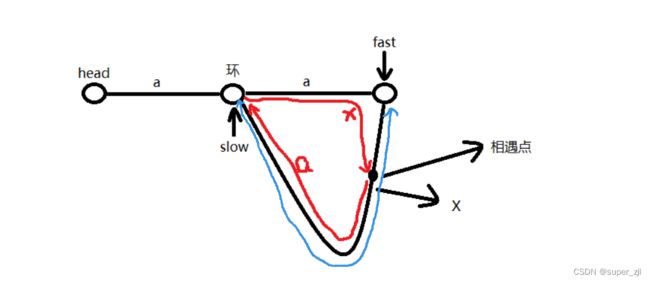
解题步骤: 1.找到相遇点 2.找对入环点 解题思路: 找到入环点关键: 相遇点到入环点距离=起始点到入环距离(相遇时一个指针往后走,另一个指针从开头走,两指针在入环点相遇) 分析: 1.fast快指针每步比slow慢指针快一步 2.当slow指针到环时距离为a,fast指针速度是slow的2倍,所以距入环点也是a,假设剩余环长度为x,所环长为a+x。 3.此时slow指针距离fast指针长度为a,fast指针追上slow指针需要追x步,每一轮fast指针会追上slow指针一步,所以入环点到相遇点的距离为x,相遇点到入环点距离=a,起始点到入环点距离也等于a。 细节:ListNode fast = head, slow = head; 快慢指针同时出发利于计算
/**
* 思路二:快慢指针
*/
public ListNode detectCycle2(ListNode head) {
if (head == null) return null;
ListNode fast = head, slow = head;
do {
//无环情况:快指针或快指针的下一个指针域指向null
if (fast == null || fast.next == null) return null;
slow = slow.next;
fast = fast.next.next;
} while (fast != slow);
fast = head;
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return fast;
}
//默认链表结构体
public class ListNode {
int val;
ListNode next;
ListNode() {
}
ListNode(int val) {
this.val = val;
}
ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
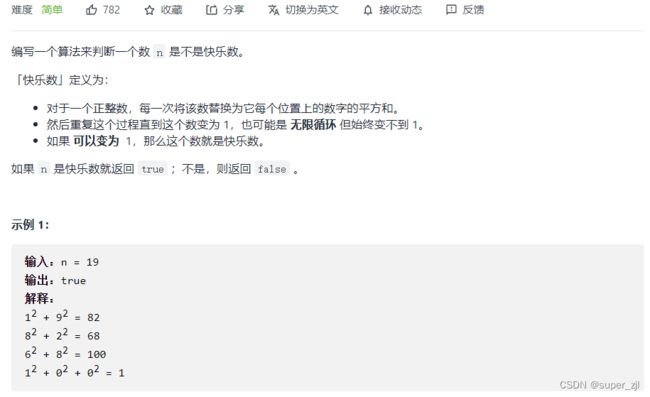
} 3.快乐数
题目
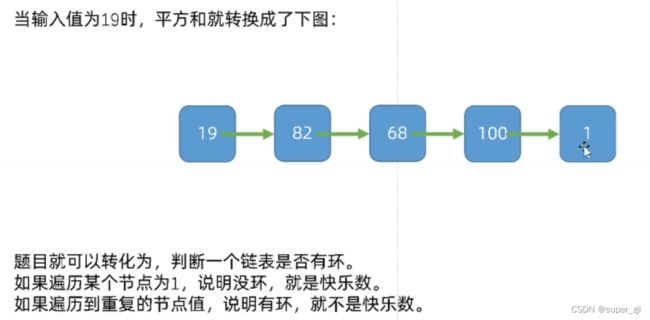
解题思路: 1.快慢指针法 2.每个位置平方和getNext方法 3.无环fast == 1 || getNext(fast) == 1时,是快乐数 3.有环,快慢指针相遇。则不是快乐数
思路一:快慢指针
/**
* 思路:快慢指针法
*/
// public static boolean isHappy(int n) {
// int fast = n, slow = n;
// do {
// //无环情况:即无无限循环且最终为1,即为快乐数
// if (fast == 1 || getNext(fast) == 1) return true;
// slow = getNext(slow);
// fast = getNext(getNext(fast));
//
// } while (fast != slow);
// //有环情况:即快慢指针相遇,有环且无限循环,所以不是快乐数
// return false;
// }
/**
* 优化
* @param n
* @return
*/
public static boolean isHappy(int n) {
int fast = n, slow = n;
do {
slow = getNext(slow);
fast = getNext(getNext(fast));
} while (fast != slow && fast != 1);
//有环情况:即快慢指针相遇,有环且无限循环,或者fast != 1,所以不是快乐数
//无环情况:循环结束后,fast = 1,是快乐数。
return fast == 1;
}
//求每个位置上的数字的平方和
public static int getNext(int n) {
int sum = 0;
while (n > 0) {
sum += (n % 10) * (n % 10);
n /= 10;
}
return sum;
}
/**
* 测试
* @param args
*/
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(isHappy(n));
}优化详解:
do {
slow = getNext(slow);
fast = getNext(getNext(fast));
} while (fast != slow && fast != 1);
//有环情况:即快慢指针相遇,有环且无限循环,或者fast != 1,所以不是快乐数
//无环情况:循环结束后,fast = 1,是快乐数。
return fast == 1;
将if (fast == 1 || getNext(fast) == 1) return true;移出来是因为并不会报空指针异常,从而减少运算次数。4.反转链表
题目
思路一:迭代-三指针移动法
public ListNode reverseList(ListNode head) {
ListNode pre = null,curr = head,next = null;
while(curr != null){
//第一步处理next指针在curr后面
next = curr.next;
//反转
curr.next = pre;
//指针向后移动
pre = curr;
curr = next;
}
//curr=null,反转结束,返回pre。
return pre;
}
//默认链表结构体
public class ListNode{
int val;
ListNode next;
ListNode(){
}
ListNode(int val){
this.val = val;
}
ListNode(int val,ListNode next){
this.val = val;
this.next = next;
}
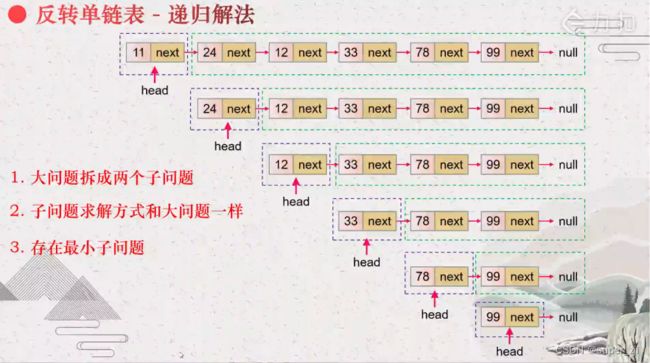
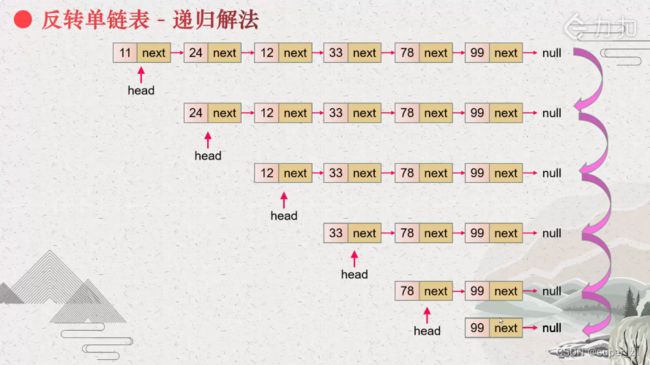
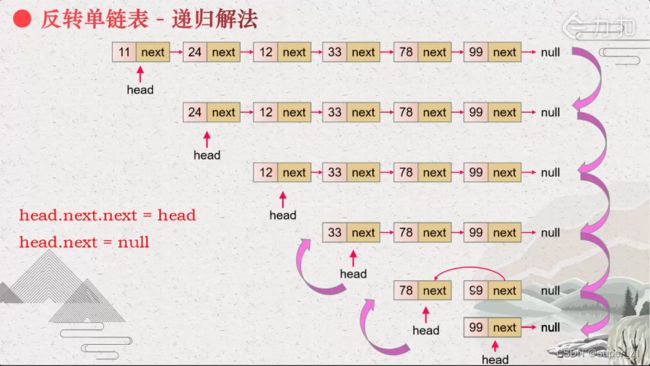
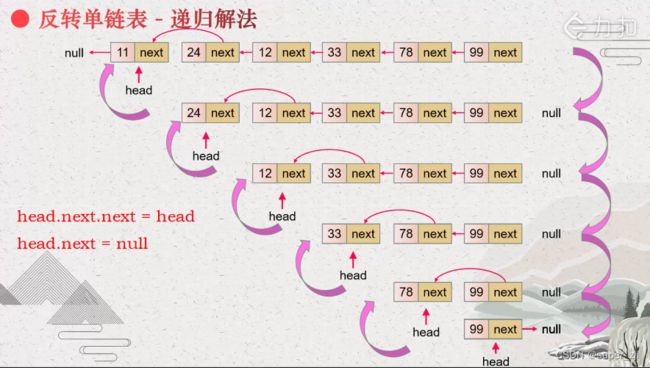
}思路二:递归
递去:
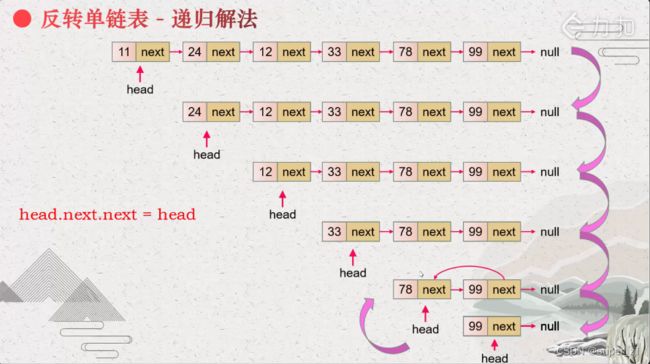
归来:子问题解决措施:head.next.next = head、head.next = null。
依次归去解决每个子问题。
public ListNode reverseList(ListNode head) {
//递归终止条件
if (head == null || head.next == null) {
return head;
}
//递归到最小子问题后,返回最小子问题的head节点。
ListNode p = reverseList(head.next);
//归来处理
head.next.next = head;
head.next = null;
//返回反转后的头节点
return p;
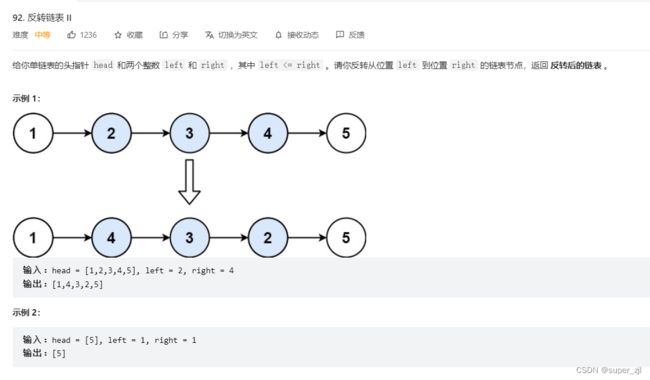
}5.反转链表 II
迭代-三指针移动法
public ListNode reverseBetween(ListNode head,int left,int right){
//创建虚拟头节点pre,con指向pre
ListNode pre = new ListNode(0,head),con =pre;
int n = right - left + 1;
//将con指向left的前一个节点
while(left > 1){
con = con.next;
left--;
}
//将[left-right]范围的几点反转,并将[left-right]的第一个节点指向[left-right]最后一个节点的下一个节点。
con.next = reverseList(con.next,n);
//返回头节点,因为pre虚拟头节点在头节点前面
return pre.next;
}
//反转[left-right]范围节点函数
public ListNode reverseList(ListNode head,int n) {
ListNode pre = null,curr = head,next = null;
//[left-right]范围需要反转的次数n
while(n > 0){
//第一步处理next指针在curr后面
next = curr.next;
//反转
curr.next = pre;
//指针向后移动
pre = curr;
curr = next;
n--;
}
//反转结束,此时curr在right.next,head.next位于left.next上。
head.next = curr;
//返回pre,pre位于right节点上
return pre;
}
//默认链表结构体
public class ListNode {
int val;
ListNode next;
ListNode() {
}
ListNode(int val) {
this.val = val;
}
ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
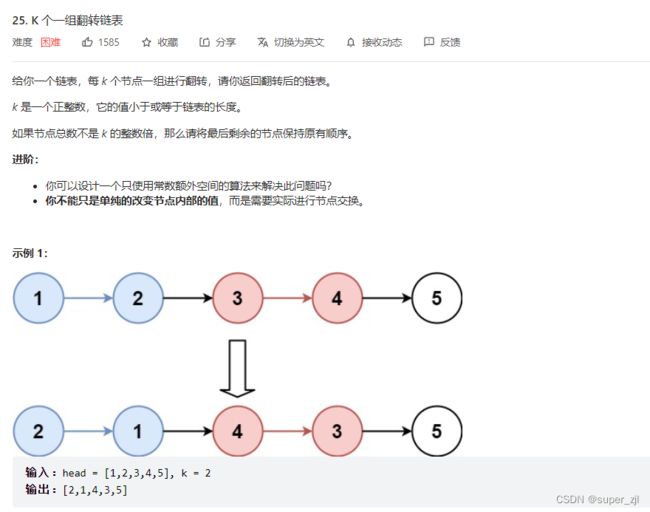
}6.k个一组翻转链表
源码:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode hair =new ListNode(0,head),pre = hair,tail = null;
while(head != null){
tail = pre;
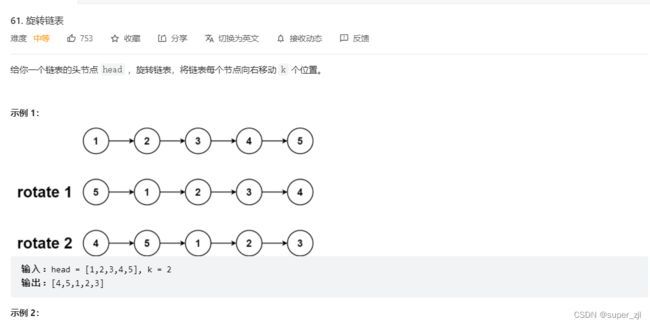
for(int i = 0;i7. 旋转链表
源码:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode rotateRight(ListNode head, int k) {
if(head == null||head.next == null) return head;
int length =1;
ListNode oldTail = head;
//计算链表长度
while(oldTail.next != null){
oldTail = oldTail.next;
length++;
}
//成环
oldTail.next = head;
//找到新的尾节点
ListNode newTail = head;
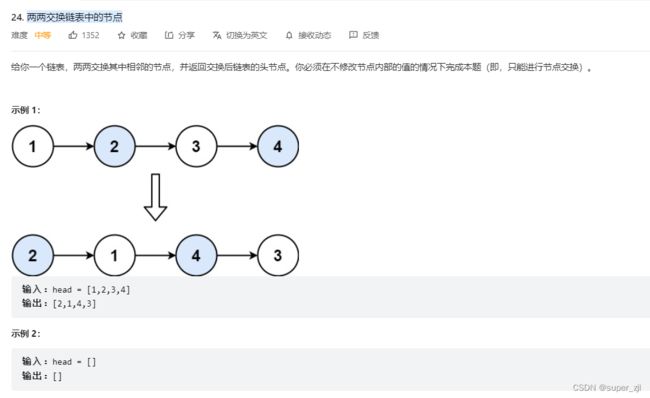
for(int i =0 ;i8.两两交换链表中的节点
源码:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode swapPairs(ListNode head) {
//定义虚拟头节点
ListNode hair = new ListNode(0,head),pre = hair;
while(pre.next != null && pre.next.next != null){
ListNode one = pre.next;
ListNode two = pre.next.next;
one.next = two.next;
two.next = one;
pre.next = two;
pre = one;
}
return hair.next;
}
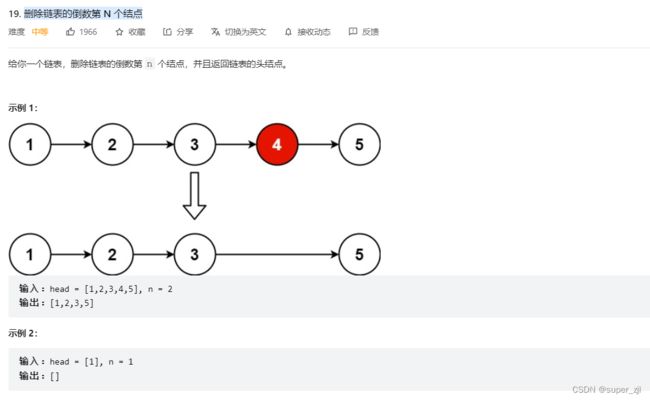
}9. 删除链表的倒数第 N 个结点
源码:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode hair = new ListNode(0,head),slow = hair, fast = head;
while(n>0){
fast = fast.next;
n--;
}
while(fast != null){
fast = fast.next;
slow = slow.next;
}
slow.next = slow.next.next;
return hair.next;
}
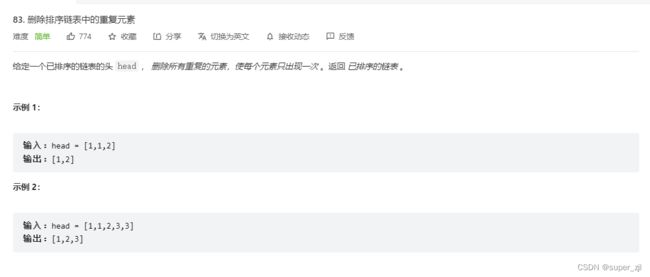
}10 . 删除排序链表中的重复元素
源码:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode deleteDuplicates(ListNode head) {
ListNode curr = head;
while(curr != null && curr.next != null){
if(curr.val == curr.next.val){
curr.next = curr.next.next;
}else{
curr = curr.next;
}
}
return head;
}
}11. 删除链表中的重复元素II
源码:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode deleteDuplicates(ListNode head) {
ListNode hair = new ListNode(0,head),pre = hair,curr = head;
while(curr != null){
while(curr.next != null && curr.val == curr.next.val){
curr = curr.next;
}
if(pre.next == curr){
pre = pre.next;
}else{
pre.next = curr.next;
}
curr = curr.next;
}
return hair.next;
}
}