离散下学期提纲

概览

• Realtions(关系)
• Semigroups and Groups(群和半群)
• Groups and coding(群和码)

---

• Advanced Counting Techniques(高级计数技巧)

---

• Groups(图)
• Trees(树)

关系

• Relations and their properties(关系及关系性质)
• n-ary relations and their applicaitons(n元关系及应用)
• Representing realtions(关系的表示)
• Closures of relations(关系闭包)
• Equivalence relations(等价关系)
• Partial Ordings(偏序关系)

群和半群

• Binary operations revisited(二元关系)
• Semigroups(半群)
• Products and Quotients of Semigroups(乘积半群和商半群)
• Groups(群)
• Products and Quotients of Groups(乘积群和商群)

群和码

• Coding of Binary Information and Error Dection
• Decoding and Error Correction

高级计数技巧

• Recurrence Relation
• Solving Recurrence Relations
• Divide-and-Conquer Algorithms and Recurrence Relations(分治算法和递归关系)
• Generating Functions(生成函数)
• Inclusion-Exclusion(容斥)
• Applications of Inclusion-Exclusion(容斥原理的应用)

图

• Graphs and Graph Models
• Graph terminology and Special Types of Graphs
• Representing Graphs and Graphs Isomorphism(图的表示和同构)
• Connectivity(连通性)
• Euler and Hamilton Path(欧拉联通与哈密顿通路)
• Shortest-path Problem(最短通路问题)
• Planar Graphs(平片图)
• Graph Coloring(图着色)

树

• Introduction to trees(树的概述)
• Application of Trees
• Tree Traversal(树的遍历)
• Spanning Trees(生成树)
• Minimum Spanning Trees(最小生成树)

大致分为三个板块：
板块一：由关系引入，到群和半群，最后是偏应用的群和码
板块二：高级计数技巧
板块三：图和树

Advanced Counting Techniques

由于很多计数问题不能用第六章(counting)讲解的方法解决。我们在这里介绍一些更高级的方法。
一些问题可以表示为递推关系和初始条件构成的序列。由与这个序列有关的等式可以得到每一项的显示公式(explicit formula)(求解递推公式)。类似的技术可以解决很多不同的计数问题。
递推关系起到重要作用的两种算法范式：动态规划(dynamic)、分治(divide-and-conquer)。(二者区别在于子问题是否重叠，重叠的叫动态规划) 同时，我们可以用递推公式求解算法复杂度。
我们还可以利用形式幂级数(也叫生成函数)来求解许多计数问题。其中x的幂的系数代表我们感兴趣的序列的项。生成函数可以用来求解递推关系式和证明组合恒等式。
还有一种方法：通过计数集合并集中元素个数来解决问题。我们将开发一种叫做容斥原理(Inclusion-Exclusion)的算法。

我们研究用递推关系构造模型的计数问题

问题类型：

• 经典递推问题：斐波那契数列、汉诺塔
• 求满足特定要求的n长度序列个数(分治思想，枚举最后一(几)位，分成不重合的小规模问题)
• 卡塔兰数序列(Catalan)$$C_n=\sum _{k=0}^{n-1}{C}_k\ast C_{n-k-1}$$

算法与递推关系：递推关系在研究一些算法和算法复杂度方面起着重要作用

8.2 求解线性递推关系

有一类重要的递推关系可以用一种系统方法明确地求解。这种递推关系中，序列的项由它的前项的线性组合来表示。

定义：k阶线性齐次递推关系
$$a_n=c_1{a}_{n-1}+c_2{a}_{n-2}+...+c_k{a}_{n-k}$$
特定递推序列由这个递推关系和k个初始条件唯一确定

说明：

• 只要满足C_k不为零就可以称为k阶的
• 齐次是指没有常数部分。
• 线性是指a_k的表示都是一次的。

求解

通过解特征方程的特征根求解递推关系的显示表示

1. 把a_k替换成r^k==>原递推关系表示为特征方程
2. 求解特征根
   2.1. 有两个不同的解：$$a_n=u{r}_1^n+v{r}_2^n$$
   2.2. 有两个相同的解：$$a_n=u{r}_1^n+nv{r}_2^n$$
3. 根据初始条件求解u,v

成立性证明同样是递推形式的

接下来给出思想核心

递推方程的解是q ^ n代表，显示表示有解H(n) = q ^ n（通解）。注意，这里当初始态不确定时，解有很多种可能。
这里肯定了一个前提：q是特征方程的特征根<==>q^n是递推方程的解（这一步是可以直接通过化简得到的）
特征根h_1(n),h_2(n)各对应线性齐次方程的一个解。也就是说它们都是该递推方程的解。
使这两个解做线性组合，这个线性组合也是递推方程的解。$$u{h}_1(n)+v{h}_2(n)$$
至于两个特征根相同时的情况同样参考二阶常系数线性齐次微分方程的解的情况

这里给出思想并不是需要记住证明方法。只是希望将各个知识点关联起来，通过理解记忆方式对固定的解题方法进行高效学习。理解了就不需要死记硬背了。
理解后的记忆：
求解线性齐次递归关系<==>求解常系数线性齐次微分方程。
(解的对应关系a_n = q ^n（通解） <==> r = q)

线性非齐次解法
也就是带常数的线性递推关系解法(其中F(n)是非齐次部分)：
$a_n=c_1{a}_{n-1}+c_1{a}_{n-2}\cdots +c_k{a}_{n-k}+F(n)$

类似求常系数线性非齐次微分方程，先求出齐次部分的通解，uv系数待定。再求非齐次部分的解。最后简单加和。
以二阶递推关系为例：

• 解齐次部分得到r1和r2，解表示为$u{r}_1+v{r}_2$, uv暂时待定
• 设非齐次部分解为n的k次方程，k为非齐次部分n的最高次幂，系数待定。（非齐次部分为$n^k$时，设设解为$C{n}^k$）
• 先将非齐次部分部分解代入递推关系求解系数。
• 齐次部分解加上非齐次解后，再求齐次部分系数。

实例说明1：$a_n=3a_{n-1}+2n$

• 设齐次解：r = 3，设$a_n^{(h)}=u{3}^n$
• 设非齐次解：n最高次为1，设解为$a_n^{(p)}=cn+d$
• 解非齐次解：令$a_n=cn+d$代入$a_n=3a_{n-1}+2n$，解得：$c=-1d=-\frac{2}{3}$
• 解齐次部分：令$a_n=-n-\frac{2}{3}+u{3}^n$解得$u=\frac{11}{6}$
• 最终解:$a_n=-n-\frac{2}{3}+\frac{11}{6}{3}^n$

实例说明2：$a_n=5a_{n-1}-6a_{n-2}+7^n$

• 与例1唯一不同的地方就在于设非齐次解，设为$C{7}^n$

8.2综上，求解线性递推关系中较特殊的齐次和非齐次线递推关系，等价于设解和求解两个主要流程，记住如何设，如何代入求待定系数即可

8.3分治算法与递推关系

分治算法：将一个大规模问题分解成若干同类型不重合小规模问题，直到规模小到问题的解可以直接求出。
分治运算次数递推关系：$f(n)=af(n/b)+g(n)$ （请自行体会与线性递推关系的关联）
这里，代表f分成几个同规模小问题，代表小规模问题的规模缩小倍数。g(n)是缩小规模需要执行的操作次数。
本章将说明如何用递推关系估计分治算法运算次数。

先附上两个定理的图：

主定理适用范围更广，通常默认n是b的整数幂次。

定理一中式子准确值：
a=1时：

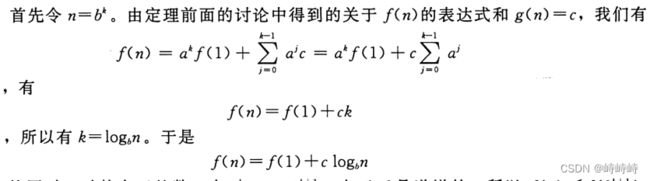
a>1时，准确值：

第一步用到2.4节几何级数求和公式：

只看结果：
$a=1时f(n)=f(1)+clo{g}_{b}n$
$a>1时f(n)=n^{lo{g}_b^a}(f(1)+\frac{c}{a-1})+\frac{-c}{a-1}$
一些题目可能会让求准确值。

本章需要记住的就是两个求分治算法复杂度的定理和分治算法准确执行步骤的式子。

8.4生成函数

直接理解生成函数可能有点困难，回顾本章开头生成函数的解释：“我们还可以利用形式幂级数(也叫生成函数)来求解许多计数问题。其中x的幂的系数代表我们感兴趣的序列的项。生成函数可以用来求解递推关系式和证明组合恒等式。”
生成函数也叫形式幂级数，可以用来解决求解递推关系和证明组合恒等式的问题。带着这个认识再去学习生成函数就可以有更清晰的学习思路，事半功倍。

定义一：

实数序列$a_0,a_1,\dots ,a_k,\dots$的生成序列是无穷级数
$$G(x)=a_0+a_{1}x+\cdots +a_k{x}^k=\sum _{k=0}^{\infty }{a}_k{x}^k$$
当{$a_n$}是有限序列时，后续补0
这样就建立了序列与生成函数（形式幂级数）之间的一一对应关系

基本思路，当生成函数可以作为计算工具使用。由于生成函数的一些性质，原本的递推关系序列可以先转化成生成函数，运算后再转化回去。
然而生成函数就其本身形式来说还是不适合运算的，需要将其转化成封闭形式，也就是用x相关的简单式子直接表示G(x)的形式

附上常见的生成函数与其封闭形式的转化，及对应的序列

只需记忆常见的几个。

此外还需要了解生成函数(幂级数)一些有用的事实

接下来就可以开始解题了。

计数问题与生成函数

应用于计数各种类型的组合数（了解）

简单形式：

并不会减少工作量，只是这种表示可能会更适合某些特殊约束，也实现了对于问题的量化表示，方便用计算机求解。

组合中有序和无序的问题

注意这里有序和无序不同的表达方式。

• 无序时只需要列举每种代币投入的个数，有几种货币就有几个乘积项
• 有序时，投入n个代币就要考虑到每次投入的情况，共n项乘积，乘积内部加和数才是代币种类数。

同样只是换了一种表示方式，有序情况中求得的封闭形式也没有什么意义，最终都是要通过枚举的方式得到结果。

同理：当题目有特殊要求时，解题方法的不同主要处理体现在生成函数的构造上。也就是关键在于如何构造一个满足题目要求的{01}序列。

生成方式求递推关系

固定步骤

• 找到序列的对应生成函数 (通常表示为$G(x)-a_0={\sum }_{k=1}^{\infty }{a}_k{x}^k$,之后代入递推关系表示$a_k$)
• 求出生成函数封闭表达式(凑递推关系中的成分,G(x)表达式中产生G(x)本身，最后表达式只留下常数和x)
• 封闭形式->递归关系的非递归表达(凑易于变形的形式，主要参照是上面的封闭形式-生成函数-序列对照表)

实例说明(a0=1)：

带有一定技巧性: 递推关系+生成函数->封闭形式->生成函数->反推递推关系序列的显示形式。

证明恒等式(了解)

8.5容斥原理

基础公式：$$|A\cup B|=|A|+|B|-|A\cap B|$$

维度拓展：$$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|C\cap B|-|A\cap C|+|A\cap B\cap C|$$

容斥原理$$|A_1\cup A_2\cup \cdots \cup A_n|=$$
$$\sum _{1<=i<=n}|A_i|-\sum _{1<=i<j<=n}|A_i\cap A_j|+\cdots +(-1{)}^n|A_1\cup A+2\cup \cdots \cup A_n|$$

有n个有限集合，它们的交中的元素个数等于
一个集合元素个数的和
减去任意两个集合的交的元素个数的和
加上任意三个集合的交的元素个数的和
。。。
$(-1{)}^n$所有集合的交的元素个数

8.6容斥原理的应用

容斥原理可以用来求解许多计数问题。
如：找出小于某个正整数的素数的个数；从一个有穷集到另一个有穷集的映射函数的个数；帽子认领问题。

容斥原理的另一种形式

这种形式可以求解一个集合中的元素个数，使得这些元素不具有n个性质$p_1,p_2,\dots ,p_n$中的任何一条性质

记：$A_i$是具有性质$p_i$的元素的子集。具有所有这些性质的元素数将记为$N(P_1,P_2,\dots ,P_n)$

则有$$N(P_1^{\prime },P_2^{\prime },\dots ,P_n^{\prime })=N-|A_1\cup A_2\cup \cdots \cup A_n|$$

代入容斥原理即可求解

用此方法主要是因为该问题求解带约束大于等于时有现成的方法求解，而小于等于时较麻烦。通过该方法把小于等于的约束问题转化成了大于等于的约束问题。

埃拉托色尼筛

求解不超过一个给定正整数的素数的个数。
一个合数可以被一个不超过它的平方根的素数整除。
不超过100的合数一定有一个不超过10的素因子。
由于小于十的素数只有2357四个素数。因此：不超过100的素数就是这四个数记忆不超过100且不被2357整除的正整数。

不超过100的正整数的个数(四个整除性质分别对应四个p)
$$4+N(p_1^{\prime }{p}_2^{\prime }{p}_3^{\prime }{p}_4^{\prime })$$

和计算机中求解方法思想一致。不过计算机中可以暴力求解该式子

求解过程：找n的小于平方根的所有素数。
用这个数量和这些素数的倍数性质构成求解式子。

映上函数的个数

从m元素集合到n元素集合的映上函数的个数。

概念补充：


映上函数等价于满射函数。

一般性定理和例题：

着重理解定理一，可能的函数个数是n${}^m$但要求映上函数时，没办法正向求解，只能从反向来考察性质，计算一定不包含某些陪集元素时可能的映射个数。

也等效于将m个元素分配给n个不可分辨的盒子。使得每个盒子都不为空。
只能求某些盒子为空时的情况数量，最后利用容斥原理求解反向条件时解的个数。

错位排列

帽子问题：将n个人的帽子随机发放给这n个人，没有一个人拿到自己的帽子的概率？
答案在于一个原始序列重新排列后没有一个元素在原始位置的排列数除以n!的值。这就是错位排列问题。

Graphs

10.1图和图模型

图的定义/类别

图的定义：图$G（V，E）$由顶点(或结点)的非空集合和边集E构成。
–
无自环,无重边：简单图Simple graph
E重复：重图/Multi-grap

有向图：E表示有向边(弧)集合。

图模型

• 社交网络
  • 交往和朋友关系图
  • 影响图
  • 合作图
• 通信网络
  • 呼叫图
• 信息网络
  • 网络图
  • 引用图
• 软件设计应用
  • 模块依赖图
  • 优先图与并发处理
• 运输图
  • 航线图
  • 道路图
• 生态网
  • 生态学中栖息地重叠图
  • 蛋白质相互作用图
• 语义网络
• 循环赛

10.2图的基本术语

基本术语

度：$deg(v)$
入度：$de{g}^{-}(v)$
出度：$de{g}^{+}(v)$

特殊简单图

• 完全图：$K_n$
  • 点:n 边:$\frac{n(n-1)}{2}$
• 圈图：$C_n$
  • 点边：n
• 轮图：$W_n$
  • 点：n+1 边：2n
• n立方体图：$Q_n$
  • 点$2^n$ 边：$n{2}^{n-1}$
• 完全二分图：$K_{m,n}$
  • 点：m+n 边：nm

图的并集

图的表示和同构

表示：

• 邻接表 Adjacency Lists
• 邻接矩阵 Adjacency Matrices
• 关联矩阵 Incidence matrices

同构的必要条件：

• 结点数相同
• 边数相同
• 度相同的结点个数相同
  (通常用于判断两个图不同构)

同构判定算法：用邻接矩阵。（可以交换行列）

10.4连通性

路径：相连的点构成的序列。

连通性Connectedness：任意两个结点之间都有路径
当不满足连通性要求时，看一个图的联通子图Connect component。
A cut vertex or cut edge：去点割点或割边，该图分成两个图。

道路定义：

• 简单道路Simple Path：道路中没有两条边是相同的
• 基本道路Element Path：道路中没有两个顶点是相同的（除起点和重点）

对于有向图：

• 强连通：有向连通
• 弱联通：去掉方向表示连通。

通过K条边从i,到j的路径条数。
用矩阵乘，几次方对应路过及条边。值是几对应有几条可选的路径。

判断n点的图的连通性。

可达性矩阵也可以作同构的判定。