词向量技术 | SkipGram词向量模型的训练以及词的余弦相似度计算

Hi，大家好啊！词向量是表示自然语言里单词的一种方法，词向量技术在自然语言处理中也有着举足轻重的作用，通过这种方法，实现把自然语言计算转换为向量计算。

---

一、词向量训练

1. 词向量计算简介

在自然语言处理任务中，词向量是表示自然语言里单词的一种方法，即把每个词都表示为一个N维空间内的点，即一个高维空间内的向量。通过这种方法，实现把自然语言计算转换为向量计算。

如 图1 所示的词向量计算任务中，先把每个词（如 queen，king 等）转换成一个高维空间的向量，这些向量在一定意义上可以代表这个词的语义信息。再通过计算这些向量之间的距离，就可以计算出词语之间的关联关系，从而达到让计算机像计算数值一样去计算自然语言的目的。

图 1  词向量计算示意图

word2vec 包含两个经典模型，CBOW（Continuous Bag-of-Words）和 Skip-gram，如 图2 所示。

• CBOW：通过上下文的词向量推理中心词。
• Skip-gram：根据中心词推理上下文。

图 2  CBOW 和 Skip-gram 语义学习示意图

2. Skip-gram 的算法实现

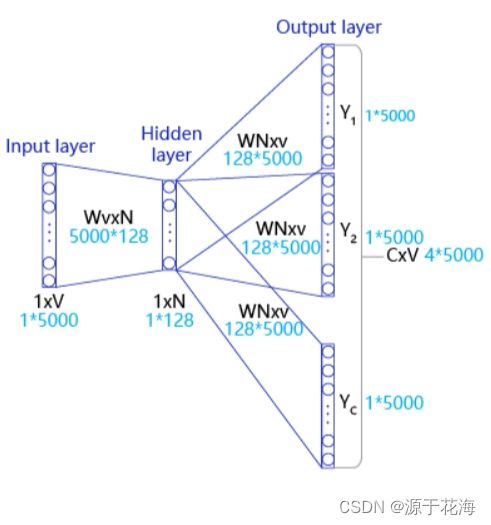
我们以 “Pineapples are spiked and yellow” 为例分别介绍Skip-gram的算法实现。如 图3 所示，Skip-gram 是一个具有 3 层结构的神经网络，分别是：

图 3  Skip-gram算法实现

• Input Layer（输入层）：接收一个 one-hot 张量 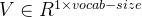 作为网络的输入，里面存储着当前句子中心词的 one-hot 表示。
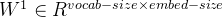• Hidden Layer（隐藏层）：将张量  乘以一个 word embedding 张量 ，并把结果作为隐藏层的输出，得到一个形状为 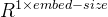的张量，里面存储着当前句子中心词的词向量。
• Output Layer（输出层）：将隐藏层的结果乘以另一个 word embedding 张量 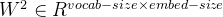，得到一个形状为  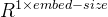的张量。这个张量经过 softmax 变换后，就得到了使用当前中心词对上下文的预测结果。根据这个 softmax 的结果，我们就可以去训练词向量模型。

在实际操作中，使用一个滑动窗口（一般情况下，长度是奇数），从左到右开始扫描当前句子。每个扫描出来的片段被当成一个小句子，每个小句子中间的词被认为是中心词，其余的词被认为是这个中心词的上下文。

3. Skip-gram 的实际实现

在实际情况中，vocab_size 通常很大（几十万甚至几百万），导致  非常大。为了缓解这个问题，通常采取负采样（negative_sampling）的方式来近似模拟多分类任务。

假设有一个中心词  和一个上下文词正样本 。在 Skip-gram 的理想实现里，需要最大化使用  推理  的概率。在使用 softmax 学习时，需要最大化  的推理概率，同时最小化其他词表中词的推理概率。之所以计算缓慢，是因为需要对词表中的所有词都计算一遍。然而我们还可以使用另一种方法，就是随机从词表中选择几个代表词，通过最小化这几个代表词的概率，去近似最小化整体的预测概率。

举个例子：先指定一个中心词（如“人工”）和一个目标词正样本（如“智能”），再随机在词表中采样几个目标词负样本（如“日本”，“喝茶”等）。有了这些内容，我们的 skip-gram 模型就变成了一个二分类任务。对于目标词正样本，我们需要最大化它的预测概率；对于目标词负样本，我们需要最小化它的预测概率。通过这种方式，我们就可以完成计算加速。上述做法，我们称之为负采样。

在实现的过程中，通常会让模型接收 3 个 tensor 输入：

• 代表中心词的 tensor：假设我们称之为 center_words ，一般来说，这个 tensor 是一个形状为 [batch_size, vocab_size] 的 one-hot tensor，表示在一个 mini-batch 中每个中心词具体的 ID。

• 代表目标词的 tensor：假设我们称之为 target_words ，一般来说，这个 tensor 同样是一个形状为 [batch_size, vocab_size] 的 one-hot tensor，表示在一个 mini-batch 中每个目标词具体的 ID。

• 代表目标词标签的 tensor：假设我们称之为 labels ，一般来说，这个 tensor 是一个形状为 [batch_size, 1] 的 tensor，每个元素不是 0 就是 1（0：负样本，1：正样本）。

---

二、余弦相似度

对于词向量 A 和 B，其余弦相似度计算公式如下：

我们知道，欧式距离注重两个词向量位置的差异，余弦相似度更看重两个词向量在方向上的差异。

首先我们一起来了解一下欧式距离的定义：随机取出两个词向量 A 和 B，A 的词向量表示为 [A1,A2,A3…An]，B的词向量表示为 [B1,B2,B3…Bn]。对于词向量A和B，其欧式距离计算公式如下：

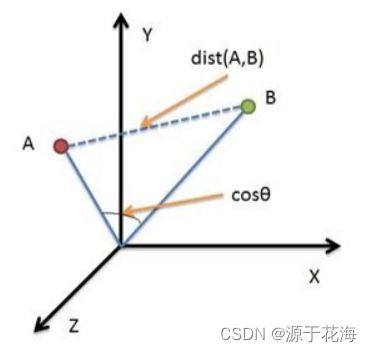
如下图所示，欧式距离    表示词向量的空间距离，余弦    显示词向量在方向上的差距。

图 4  欧式距离和余弦在词向量中的表示

举个例子：
X 和 Y 用户对两个内容评分，按 5 分制，X 用户对内容 1 和内容 2 的评分分别为 1 和 4，Y 用户对内容 1 和内容 2 的评分分别为 2 和 5。令 A=[1,2]，B=[4,5]。此时 dist(A,B)=4.24，在 5 分制的评级中，该距离较大，表示用户对内容 1 和 2 的总体看法区别较大。cosθ=0.99，余弦相似度较大，表示两个用户的偏好基本一致，即相对于内容 1，两个用户都稍加喜欢内容 2。

---

三、使用飞桨实现 Skip-gram

接下来我们将学习使用飞桨实现 Skio-gram 模型的方法。在飞桨中，不同深度学习模型的训练过程基本一致，流程如下：

• 数据处理：选择需要使用的数据，并做好必要的预处理工作。
• 网络定义：使用飞桨定义好网络结构，包括输入层，中间层，输出层，损失函数和优化算法。
• 网络训练：将准备好的数据送入神经网络进行学习，并观察学习的过程是否正常，如损失函数值是否在降低，也可以打印一些中间步骤的结果出来等。
• 网络评估：使用测试集合测试训练好的神经网络，看看训练效果如何。

在数据处理前，需要先加载飞桨平台（如果用户在本地使用，请确保已经安装飞桨）。

import io
import os
import sys
import requests
import math
import random
import numpy as np
import paddle

1. 数据处理

首先，找到一个合适的语料用于训练word2vec模型。我们选择text8数据集，这个数据集里包含了大量从维基百科收集到的英文语料，我们可以通过如下代码下载数据集，下载后的文件被保存在当前目录的 text8.txt 文件内。

# 下载语料用来训练word2vec
def download():
    # 可以从百度云服务器下载一些开源数据集（dataset.bj.bcebos.com）
    corpus_url = "https://dataset.bj.bcebos.com/word2vec/text8.txt"
    # 使用python的requests包下载数据集到本地
    web_request = requests.get(corpus_url)
    corpus = web_request.content
    # 把下载后的文件存储在当前目录的text8.txt文件内
    with open("./text8.txt", "wb") as f:
        f.write(corpus)
    f.close()

download()

接下来，把下载的语料读取到程序里，并打印前 500 个字符看看语料的样子，代码如下：

# 读取text8数据
def load_text8():
    with open("./text8.txt", "r") as f:
        corpus = f.read().strip("\n")
    f.close()

    return corpus

corpus = load_text8()

# 打印前500个字符，简要看一下这个语料的样子
print(corpus[:500])

一般来说，在自然语言处理中，需要先对语料进行切词。对于英文来说，可以比较简单地直接使用空格进行切词，代码如下：

# 对语料进行预处理（分词）
def data_preprocess(corpus):
    # 由于英文单词出现在句首的时候经常要大写，所以我们把所有英文字符都转换为小写，
    # 以便对语料进行归一化处理（Apple vs apple等）
    corpus = corpus.strip().lower()
    corpus = corpus.split(" ")

    return corpus

corpus = data_preprocess(corpus)
print(corpus[:50])

在经过切词后，需要对语料进行统计，为每个词构造ID。一般来说，可以根据每个词在语料中出现的频次构造ID，频次越高，ID越小，便于对词典进行管理。代码如下：

# 构造词典，统计每个词的频率，并根据频率将每个词转换为一个整数id
def build_dict(corpus):
    #首先统计每个不同词的频率（出现的次数），使用一个词典记录
    word_freq_dict = dict()
    for word in corpus:
        if word not in word_freq_dict:
            word_freq_dict[word] = 0
        word_freq_dict[word] += 1

    # 将这个词典中的词，按照出现次数排序，出现次数越高，排序越靠前
    # 一般来说，出现频率高的高频词往往是：I，the，you这种代词，而出现频率低的词，往往是一些名词，如：nlp
    word_freq_dict = sorted(word_freq_dict.items(), key = lambda x:x[1], reverse = True)
    
    # 构造3个不同的词典，分别存储，
    # 每个词到id的映射关系：word2id_dict
    # 每个id出现的频率：word2id_freq
    # 每个id到词典映射关系：id2word_dict
    word2id_dict = dict()
    word2id_freq = dict()
    id2word_dict = dict()

    # 按照频率，从高到低，开始遍历每个单词，并为这个单词构造一个独一无二的id
    for word, freq in word_freq_dict:
        curr_id = len(word2id_dict)
        word2id_dict[word] = curr_id
        word2id_freq[word2id_dict[word]] = freq
        id2word_dict[curr_id] = word

    return word2id_freq, word2id_dict, id2word_dict

word2id_freq, word2id_dict, id2word_dict = build_dict(corpus)
vocab_size = len(word2id_freq)
print("there are totoally %d different words in the corpus" % vocab_size)
for _, (word, word_id) in zip(range(50), word2id_dict.items()):
    print("word %s, its id %d, its word freq %d" % (word, word_id, word2id_freq[word_id]))

得到 word2id 词典后，我们还需要进一步处理原始语料，把每个词替换成对应的ID，便于神经网络进行处理，代码如下：

# 把语料转换为id序列
def convert_corpus_to_id(corpus, word2id_dict):
    # 使用一个循环，将语料中的每个词替换成对应的id，以便于神经网络进行处理
    corpus = [word2id_dict[word] for word in corpus]
    return corpus

corpus = convert_corpus_to_id(corpus, word2id_dict)
print("%d tokens in the corpus" % len(corpus))
print(corpus[:50])

接下来，需要使用二次采样法处理原始文本。二次采样法的主要思想是降低高频词在语料中出现的频次，降低的方法是随机将高频的词抛弃，频率越高，被抛弃的概率就越高，频率越低，被抛弃的概率就越低，这样像标点符号或冠词这样的高频词就会被抛弃，从而优化整个词表的词向量训练效果，代码如下：

# 使用二次采样算法（subsampling）处理语料，强化训练效果
def subsampling(corpus, word2id_freq):
    
    # 这个discard函数决定了一个词会不会被替换，这个函数是具有随机性的，每次调用结果不同
    # 如果一个词的频率很大，那么它被遗弃的概率就很大
    def discard(word_id):
        return random.uniform(0, 1) < 1 - math.sqrt(
            1e-4 / word2id_freq[word_id] * len(corpus))

    corpus = [word for word in corpus if not discard(word)]
    return corpus

corpus = subsampling(corpus, word2id_freq)
print("%d tokens in the corpus" % len(corpus))
print(corpus[:50])

在完成语料数据预处理之后，需要构造训练数据。根据上面的描述，我们需要使用一个滑动窗口对语料从左到右扫描，在每个窗口内，中心词需要预测它的上下文，并形成训练数据。

在实际操作中，由于词表往往很大（50000，100000等），对大词表的一些矩阵运算（如softmax）需要消耗巨大的资源，因此可以通过负采样的方式模拟softmax的结果，代码实现如下。

• 给定一个中心词和一个需要预测的上下文词，把这个上下文词作为正样本。
• 通过词表随机采样的方式，选择若干个负样本。
• 把一个大规模分类问题转化为一个 2 分类问题，通过这种方式优化计算速度。

# 构造数据，准备模型训练
# max_window_size代表了最大的window_size的大小，程序会根据max_window_size从左到右扫描整个语料
# negative_sample_num代表了对于每个正样本，我们需要随机采样多少负样本用于训练，
# 一般来说，negative_sample_num的值越大，训练效果越稳定，但是训练速度越慢。 
def build_data(corpus, word2id_dict, word2id_freq, max_window_size = 3, 
               negative_sample_num = 4):
    
    # 使用一个list存储处理好的数据
    dataset = []
    center_word_idx=0

    # 从左到右，开始枚举每个中心点的位置
    while center_word_idx < len(corpus):
        # 以max_window_size为上限，随机采样一个window_size，这样会使得训练更加稳定
        window_size = random.randint(1, max_window_size)
        # 当前的中心词就是center_word_idx所指向的词，可以当作正样本
        positive_word = corpus[center_word_idx]

        # 以当前中心词为中心，左右两侧在window_size内的词就是上下文
        context_word_range = (max(0, center_word_idx - window_size), min(len(corpus) - 1, center_word_idx + window_size))
        context_word_candidates = [corpus[idx] for idx in range(context_word_range[0], context_word_range[1]+1) if idx != center_word_idx]

        # 对于每个正样本来说，随机采样negative_sample_num个负样本，用于训练
        for context_word in context_word_candidates:
            # 首先把（上下文，正样本，label=1）的三元组数据放入dataset中，
            # 这里label=1表示这个样本是个正样本
            dataset.append((context_word, positive_word, 1))

            # 开始负采样
            i = 0
            while i < negative_sample_num:
                negative_word_candidate = random.randint(0, vocab_size-1)

                if negative_word_candidate is not positive_word:
                    # 把（上下文，负样本，label=0）的三元组数据放入dataset中，
                    # 这里label=0表示这个样本是个负样本
                    dataset.append((context_word, negative_word_candidate, 0))
                    i += 1
        
        center_word_idx = min(len(corpus) - 1, center_word_idx + window_size)
        if center_word_idx == (len(corpus) - 1):
            center_word_idx += 1
        if center_word_idx % 100000 == 0:
            print(center_word_idx)
    
    return dataset

dataset = build_data(corpus, word2id_dict, word2id_freq)
for _, (context_word, target_word, label) in zip(range(50), dataset):
    print("center_word %s, target %s, label %d" % (id2word_dict[context_word],
                                                   id2word_dict[target_word], label))

训练数据准备好后，把训练数据都组装成mini-batch，并准备输入到网络中进行训练，代码如下：

# 构造mini-batch，准备对模型进行训练
# 我们将不同类型的数据放到不同的tensor里，便于神经网络进行处理
# 并通过numpy的array函数，构造出不同的tensor来，并把这些tensor送入神经网络中进行训练
def build_batch(dataset, batch_size, epoch_num):
    
    #center_word_batch缓存batch_size个中心词
    center_word_batch = []
    #target_word_batch缓存batch_size个目标词（可以是正样本或者负样本）
    target_word_batch = []
    #label_batch缓存了batch_size个0或1的标签，用于模型训练
    label_batch = []

    for epoch in range(epoch_num):
        # 每次开启一个新epoch之前，都对数据进行一次随机打乱，提高训练效果
        random.shuffle(dataset)
        
        for center_word, target_word, label in dataset:
            #遍历dataset中的每个样本，并将这些数据送到不同的tensor里
            center_word_batch.append([center_word])
            target_word_batch.append([target_word])
            label_batch.append(label)

            # 当样本积攒到一个batch_size后，我们把数据都返回回来
            # 在这里我们使用numpy的array函数把list封装成tensor
            # 并使用python的迭代器机制，将数据yield出来
            # 使用迭代器的好处是可以节省内存
            if len(center_word_batch) == batch_size:
                yield np.array(center_word_batch).astype("int64"), \
                    np.array(target_word_batch).astype("int64"), \
                    np.array(label_batch).astype("float32")
                center_word_batch = []
                target_word_batch = []
                label_batch = []

    if len(center_word_batch) > 0:
        yield np.array(center_word_batch).astype("int64"), \
            np.array(target_word_batch).astype("int64"), \
            np.array(label_batch).astype("float32")

# for _, batch in zip(range(10), build_batch(dataset, 128, 3)):
#     print(batch)

2. 网络定义

定义 skip-gram 的网络结构，用于模型训练。在飞桨动态图中，对于任意网络，都需要定义一个继承自 paddle.nn.Layer 的类来搭建网络结构、参数等数据的声明。同时需要在 forward 函数中定义网络的计算逻辑。值得注意的是，我们仅需要定义网络的前向计算逻辑，飞桨会自动完成神经网络的反向计算，代码如下：

# 定义skip-gram训练网络结构
# 这里我们使用的是paddlepaddle的2.0.0版本
# 一般来说，在使用nn训练的时候，我们需要通过一个类来定义网络结构，这个类继承了paddle.nn.Layer
class SkipGram(paddle.nn.Layer):
    def __init__(self, vocab_size, embedding_size, init_scale=0.1):
        # vocab_size定义了这个skipgram这个模型的词表大小
        # embedding_size定义了词向量的维度是多少
        # init_scale定义了词向量初始化的范围，一般来说，比较小的初始化范围有助于模型训练
        super(SkipGram, self).__init__()
        self.vocab_size = vocab_size
        self.embedding_size = embedding_size

        # 使用paddle.nn提供的Embedding函数，构造一个词向量参数
        # 这个参数的大小为：self.vocab_size, self.embedding_size
        # 这个参数的名称为：embedding_para
        # 这个参数的初始化方式为在[-init_scale, init_scale]区间进行均匀采样
        self.embedding = paddle.nn.Embedding(
            self.vocab_size, 
            self.embedding_size,
            weight_attr=paddle.ParamAttr(
                name='embedding_para',
                initializer=paddle.nn.initializer.Uniform(
                    low=-0.5/embedding_size, high=0.5/embedding_size)))

        # 使用paddle.nn提供的Embedding函数，构造另外一个词向量参数
        # 这个参数的大小为：self.vocab_size, self.embedding_size
        # 这个参数的名称为：embedding_para_out
        # 这个参数的初始化方式为在[-init_scale, init_scale]区间进行均匀采样
        # 跟上面不同的是，这个参数的名称跟上面不同，因此，
        # embedding_para_out和embedding_para虽然有相同的shape，但是权重不共享
        self.embedding_out = paddle.nn.Embedding(
            self.vocab_size, 
            self.embedding_size,
            weight_attr=paddle.ParamAttr(
                name='embedding_out_para',
                initializer=paddle.nn.initializer.Uniform(
                    low=-0.5/embedding_size, high=0.5/embedding_size)))

    # 定义网络的前向计算逻辑
    # center_words是一个tensor（mini-batch），表示中心词
    # target_words是一个tensor（mini-batch），表示目标词
    # label是一个tensor（mini-batch），表示这个词是正样本还是负样本（用0或1表示）
    # 用于在训练中计算这个tensor中对应词的同义词，用于观察模型的训练效果
    def forward(self, center_words, target_words, label):
        # 首先，通过embedding_para（self.embedding）参数，将mini-batch中的词转换为词向量
        # 这里center_words和eval_words_emb查询的是一个相同的参数
        # 而target_words_emb查询的是另一个参数
        center_words_emb = self.embedding(center_words)
        target_words_emb = self.embedding_out(target_words)

        # center_words_emb = [batch_size, embedding_size]
        # target_words_emb = [batch_size, embedding_size]
        # 我们通过点乘的方式计算中心词到目标词的输出概率，并通过sigmoid函数估计这个词是正样本还是负样本的概率。
        word_sim = paddle.multiply(center_words_emb, target_words_emb)
        word_sim = paddle.sum(word_sim, axis = -1)
        word_sim = paddle.reshape(word_sim, shape=[-1])
        pred = paddle.nn.functional.sigmoid(word_sim)

        # 通过估计的输出概率定义损失函数，注意我们使用的是binary_cross_entropy函数
        # 将sigmoid计算和cross entropy合并成一步计算可以更好的优化，所以输入的是word_sim，而不是pred
        
        loss = paddle.nn.functional.binary_cross_entropy(paddle.nn.functional.sigmoid(word_sim), label)
        loss = paddle.mean(loss)

        # 返回前向计算的结果，飞桨会通过backward函数自动计算出反向结果。
        return pred, loss

3. 网络训练

完成网络定义后，就可以启动模型训练。我们定义每隔100步打印一次Loss，以确保当前的网络是正常收敛的。同时，我们每隔1000步观察一下skip-gram计算出来的同义词（使用 embedding的乘积），可视化网络训练效果，代码如下：

# 开始训练，定义一些训练过程中需要使用的超参数
batch_size = 512
epoch_num = 1
embedding_size = 200
step = 0
learning_rate = 0.001

# 定义一个使用word-embedding计算cos的函数
def get_cos(query1_token, query2_token, embed):
    W = embed
    x = W[word2id_dict[query1_token]]
    y = W[word2id_dict[query2_token]]
    cos = np.dot(x, y) / np.sqrt(np.sum(y * y) * np.sum(x * x) + 1e-9)
    flat = cos.flatten()
    print("单词1 %s 和单词2 %s 的cos结果为 %f" %(query1_token, query2_token, cos))


# 通过我们定义的SkipGram类，来构造一个Skip-gram模型网络
skip_gram_model = SkipGram(vocab_size, embedding_size)
# 构造训练这个网络的优化器
adam = paddle.optimizer.Adam(learning_rate=learning_rate, parameters = skip_gram_model.parameters())

# 使用build_batch函数，以mini-batch为单位，遍历训练数据，并训练网络
for center_words, target_words, label in build_batch(
    dataset, batch_size, epoch_num):
    # 使用paddle.to_tensor函数，将一个numpy的tensor，转换为飞桨可计算的tensor
    center_words_var = paddle.to_tensor(center_words)
    target_words_var = paddle.to_tensor(target_words)
    label_var = paddle.to_tensor(label)

    # 将转换后的tensor送入飞桨中，进行一次前向计算，并得到计算结果
    pred, loss = skip_gram_model(
        center_words_var, target_words_var, label_var)

    # 通过backward函数，让程序自动完成反向计算
    loss.backward()
    # 通过minimize函数，让程序根据loss，完成一步对参数的优化更新
    adam.minimize(loss)
    # 使用clear_gradients函数清空模型中的梯度，以便于下一个mini-batch进行更新
    skip_gram_model.clear_gradients()

    # 每经过100个mini-batch，打印一次当前的loss，看看loss是否在稳定下降
    step += 1
    if step % 100 == 0:
        print("step %d, loss %.3f" % (step, loss.numpy()[0]))

    # 经过10000个mini-batch，打印一次模型对eval_words中的10个词计算的同义词
    # 这里我们使用词和词之间的向量点积作为衡量相似度的方法
    # 我们只打印了5个最相似的词
    if step % 2000 == 0:
        embedding_matrix = skip_gram_model.embedding.weight.numpy()
        np.save("./embedding", embedding_matrix)
        get_cos("king","queen",embedding_matrix)
        get_cos("she","her",embedding_matrix)
        get_cos("topic","theme",embedding_matrix)
        get_cos("woman","game",embedding_matrix)
        get_cos("one","name",embedding_matrix)        

从打印结果可以看到，经过一定步骤的训练，Loss 逐渐下降并趋于稳定。

4. 词向量结果评价

我们采用余弦相似度计算来对词向量结果进行评价，代码如下：

# 定义一个使用word-embedding计算cos的函数
def get_cos(query1_token, query2_token, embed):
    W = embed
    x = W[word2id_dict[query1_token]]
    y = W[word2id_dict[query2_token]]
    cos = np.dot(x, y) / np.sqrt(np.sum(y * y) * np.sum(x * x) + 1e-9)
    flat = cos.flatten()
    print("单词1 %s 和单词2 %s 的cos结果为 %f" %(query1_token, query2_token, cos) )

embedding_matrix = np.load('embedding.npy') 
get_cos("king","queen",embedding_matrix)
get_cos("she","her",embedding_matrix)
get_cos("topic","theme",embedding_matrix)
get_cos("woman","game",embedding_matrix)
get_cos("one","name",embedding_matrix)