数据结构(JS实现)
目录
- 链表
-
- 链表的特点
- 链表中的常见操作
- 单链表
-
- append(data)尾部追加新节点
- toString()输出链表的节点数据
- 插入节点insert(position,data)
- get(position)获取链表指定位置节点的数据
- indexOf(data)查找对应数据节点的位置
- update(position, newData)更新指定位置节点数据
- removeAt(position)删除指定位置的节点
- remove(data)删除第一个数据为data的节点
- isEmpty()判断链表是否为空
- size()返回链表长度
- 单链表构造函数完整实现
- 经典相关算法题
-
- 链表反转
- 数组
- 哈希表/散列表
- 树
-
- 完美二叉树(Perfect Binary Tree)/满二叉树(Full Binary Tree)
- 完全二叉树(Compelete Binary Tree)
- 二叉搜索树/二叉查找树/二叉排序树(Binary Search Tree,简称BST)
链表
与数组不同,我们无法在常量时间内访问单链表中的随机元素。 如果我们想要获得第 i 个元素,我们必须从头结点逐个遍历。 我们按索引来访问元素平均要花费 O(N) 时间,其中 N 是链表的长度。
- 查找时间复杂度:O(n)
创建单向链表类
// 封装链表的构造函数
function LinkedList() {
//封装一个Node类,用于保存每个节点信息
function Node(data,next) {
this.data = data
this.next = (next===undefined ? null : next)
}
// 链表中的属性
this.length = 0 // 链表的长度
this.head = null //链表的第一个节点
}
ES6
class LinkedList{
constructor Node(data,next) {
this.data = data
this.next = (next===undefined ? null : next)
// 链表中的属性
this.length = 0 // 链表的长度
this.head = null //链表的第一个节点
}
}
链表的特点
链表和数组一样,可以用于存储一系列的元素,但是链表和数组的实现机制完全不同。链表的每个元素由一个存储元素本身的节点和一个指向下一个元素的引用(有的语言称为指针或连接)组成。类似于火车头,一节车厢载着乘客(数据),通过节点连接另一节车厢。


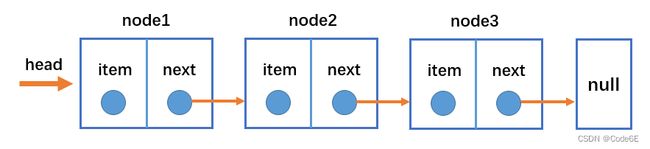
- head属性指向链表的第一个节点;
- 链表中的最后一个节点指向null;
- 当链表中一个节点也没有的时候,head直接指向null;
数组存在的缺点:
数组的创建通常需要申请一段连续的内存空间(一整块内存),并且大小是固定的。所以当原数组不能满足容量需求时,需要扩容(一般情况下是申请一个更大的数组,比如2倍,然后将原数组中的元素复制过去)。
在数组的开头或中间位置插入数据的成本很高,需要进行大量元素的位移。
链表的优势:
链表中的元素在内存中不必是连续的空间,可以充分利用计算机的内存,实现灵活的内存动态管理。
链表不必在创建时就确定大小,并且大小可以无限地延伸下去。
链表在插入和删除数据时,时间复杂度可以达到O(1),相对数组效率高很多。
链表的缺点:
链表访问任何一个位置的元素时,都需要从头开始访问(无法跳过第一个元素访问任何一个元素)。
无法通过下标值直接访问元素,需要从头开始一个个访问,直到找到对应的元素。
虽然可以轻松地到达下一个节点,但是回到前一个节点是很难的(单链表比较困难,双链表简单)。
链表中的常见操作
函数名是自定义的
append(element):向链表尾部添加一个新的项;
insert(position,element):向链表的特定位置插入一个新的项;
get(position):获取对应位置的元素;
indexOf(element):返回元素在链表中的索引。如果链表中没有该元素就返回-1;
update(position,element):修改某个位置的元素;
removeAt(position):从链表的特定位置移除一项;
remove(element):从链表中移除一项;
isEmpty():如果链表中不包含任何元素,返回trun,如果链表长度大于0则返回false;
size():返回链表包含的元素个数,与数组的length属性类似;
toString():由于链表项使用了Node类,就需要重写继承自JavaScript对象默认的toString方法,让其只输出元素的值;
单链表
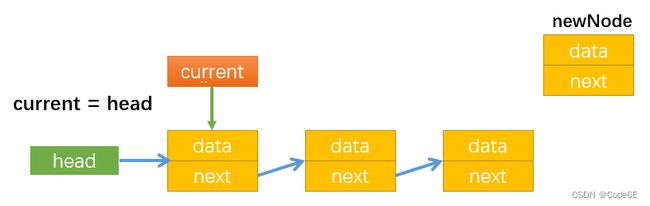
append(data)尾部追加新节点
// 封装链表的构造函数
function LinkedList() {
//封装一个Node类,用于保存每个节点信息
function Node(data,next) {
this.data = data
this.next = (next===undefined ? null : next)
}
// 链表中的属性
this.length = 0 // 链表的长度
this.head = null //链表的第一个节点
//链表中的方法
// 1.追加节点的方法append,追加是指在链表的末尾添加节点
LinkedList.prototype.append = function (data) {
// 首先创建节点
let newNode = new Node(data)
// 然后找到末尾的节点,将新创建的节点添加到末尾
// 如果是空链,直接让头指针指向新节点
if (this.length == 0) {
this.head = newNode
} else {
// 从头开始查找,用current标记当前查找的位置
let current = this.head
// if(current==null) current=newNode // 也可以这样判断链表目前是否是空链
// 否则查找链表的最后一个节点
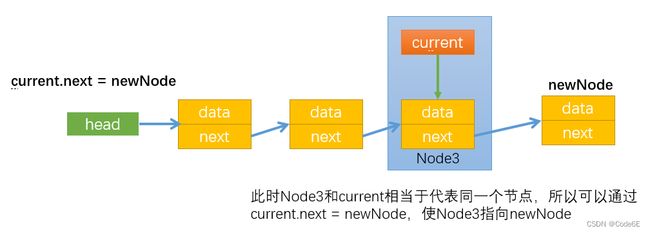
while (current.next) {
current = current.next
}
// 最后一个节点的current.next==null,所以会跳出while循环
// 让最后一个节点指向新节点
current.next = newNode
}
// 链表长度加一
this.length += 1
}
}
过程详解:
//测试代码
//1.创建LinkedList
let list = new LinkedList()
//2.测试append方法
list.append('aaa')
list.append('bbb')
list.append('ccc')
console.log(list);
toString()输出链表的节点数据
代码实现:
LinkedList.prototype.toString =function(){
let current=this.head
// listString存储链表的节点数据
let listString=''
// 空链表不会进入该循环,content为空
while(current){
listString += current.data+' '// 每个节点数据后加个空格,便于阅读
current=current.next
}
return listString
}
测试代码
//测试代码
//1.创建LinkedList
let list = new LinkedList()
//2.插入数据
list.append('aaa')
list.append('bbb')
list.append('ccc')
//3.测试toString方法
console.log(list.toString());
插入节点insert(position,data)
代码
// position的有效范围是整数[0,length]
LinkedList.prototype.insert=function(position,data){
let newNode=new Node(data)
if(position<0|| position>=this.length){
// false表示插入失败
return false;
}else if(position==0){//newNode成为头结点的情况
// 注意顺序不能颠倒
newNode.next=this.head
this.head=newNode
}else{
// 包含newNode成为最后一个节点的情况,与插入在中间位置一样的操作
let current=this.head
// 找到newNode要插入位置的前一个节点,跳出循环后current指向该节点
for(let i=0;i<position;i++){
current=current.next
}
// 顺序不能颠倒
newNode.next=current.next
current.next=newNode
}
this.length+=1
// true表示插入成功
return true
}
过程详解:
position是节点插入链表后所处的位置,其有效范围是整数[0,length],根据插入节点位置的不同可分为多种情况:
情况1:position = 0:
通过: newNode.next = this.head,建立连接1;
通过: this.head = newNode,建立连接2;(不能先建立连接2,否则this.head不再指向Node1)
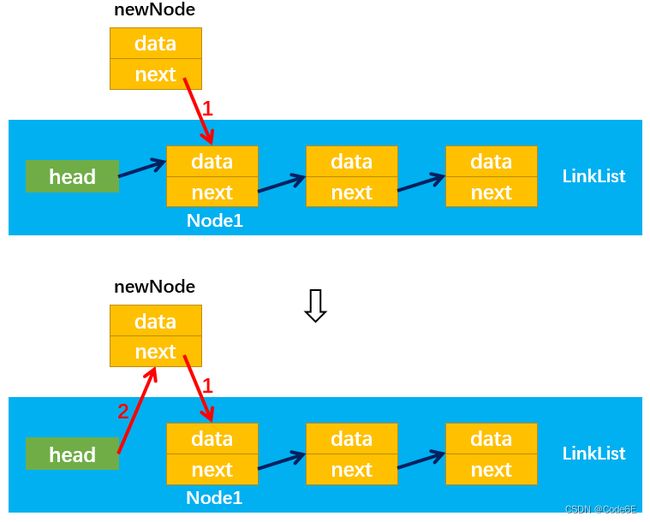
情况2:position > 0:

// 包含newNode成为最后一个节点的情况,与插入在中间位置一样的操作
let current=this.head
// 找到newNode要插入位置的前一个节点,跳出循环后current指向该节点
for(let i=0;i<position;i++){
current=current.next
}
// 顺序不能颠倒
newNode.next=current.next
current.next=newNode
测试代码
//1.创建LinkedList
let list = new LinkedList()
//2.插入数据
list.append('aaa')
list.append('bbb')
list.append('ccc')
//3.测试insert方法
list.insert(0, '在链表最前面插入节点');
list.insert(2, '在链表中第二个节点后插入节点');
list.insert(5, '在链表最后插入节点');
alert(list)// alert会自动调用参数的toString方法
console.log(list);
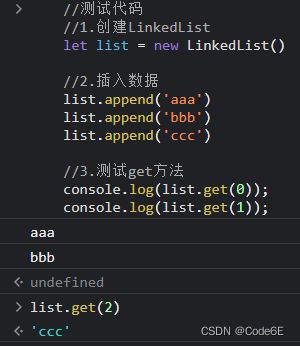
get(position)获取链表指定位置节点的数据
//测试代码
//1.创建LinkedList
let list = new LinkedList()
//2.插入数据
list.append('aaa')
list.append('bbb')
list.append('ccc')
//3.测试get方法
console.log(list.get(0));
console.log(list.get(1));
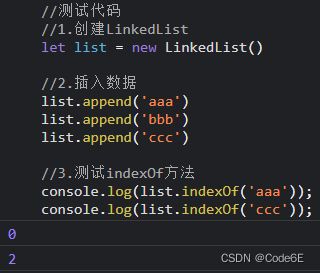
indexOf(data)查找对应数据节点的位置
代码
// 根据数据查询数据所在链表位置
LinkedList.prototype.indexOf=function(data){
let current= this.head
let index=0
// 从头结点开始逐个查找数据等于data的节点
while(current){
if(current.data==data){
return index
}
current=current.next
index+=1
}
// 没有查找到就返回-1
return -1
}
测试代码
//测试代码
//1.创建LinkedList
let list = new LinkedList()
//2.插入数据
list.append('aaa')
list.append('bbb')
list.append('ccc')
//3.测试indexOf方法
console.log(list.indexOf('aaa'));
console.log(list.indexOf('ccc'));
update(position, newData)更新指定位置节点数据
代码
LinkedList.prototype.update=function(position,newData){
// position有效取值是[0,this.length-1]间的整数,修改失败返回false
if(position<0|| position>=this.length) return false;
let current=this.head
let i=0
// 遍历至处于position位置的节点
while(i++<position){
current=current.next
}
// console.log(i); //position=2时,i=3,说明跳出循环i还是会自增1,因为自增运算符比比较运算符优先级高
// 跳出循环时,current已经指向处于position位置的节点
current.data=newData
return true
}
测试代码
//1.创建LinkedList
let list = new LinkedList()
//2.插入数据
list.append('aaa')
list.append('bbb')
list.append('ccc')
//3.测试update方法
console.log(list.update(0, '修改第0个节点'))
console.log(list.update(2, '修改第2个节点'))
console.log(list.update(3, '超出范围无法修改'));
console.log(list.toString());
removeAt(position)删除指定位置的节点
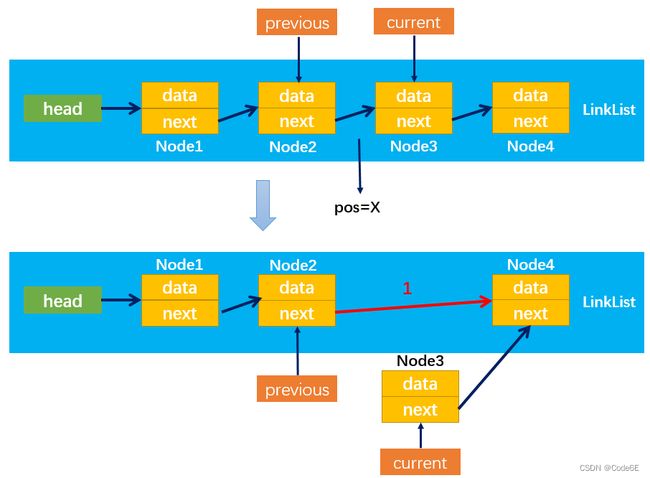
情况1:position = 0,即移除第一个节点(Node1)。通过:this.head = this.head.next,改变指向1即可;虽然Node1的next仍指向Node2,但是没有引用指向Node1,则Node1会被垃圾回收器自动回收,所以不用处理Node1指向Node2的引用next。

情况2:positon > 0,比如pos = 2即移除第三个节点(Node3)。
首先,定义两个变量previous和curent分别指向需要删除位置pos = x的前一个节点和当前要删除的节点;
然后,通过:previous.next = current.next,改变指向1即可;
随后,没有引用指向Node3,Node3就会被自动回收,至此成功删除Node3 。
代码
LinkedList.prototype.removeAt=function(position){
// 超出范围的删除不了
if(position<0|| position>=this.length) return false;
let current =this.head
// 如果删除第一个节点
if(position==0){
this.head=this.head.next
}else{
let i=0;
let previous=this.head
while(i++<position){
previous=current
current=current.next
}
previous.next=current.next
this.length--;
}
return current.data
}
测试代码
let list = new LinkedList()
//2.插入数据
list.append('aaa')
list.append('bbb')
list.append('ccc')
//3.测试removeAt方法
console.log(list.removeAt(0));
console.log(list.removeAt(1));
console.log(list);
remove(data)删除第一个数据为data的节点
LinkedList.prototype.remove=function(data){
let current= this.head
let index=0
let previous=this.head
// 从头结点开始逐个查找数据等于data的节点
while(current){
if(current.data==data){
// 如果删除的是头节点
if(index==0){
this.head=this.head.next
}else{
previous.next=current.next
}
this.length--;
return index
}
// previous和current指向下一个节点
previous=current
current=current.next
index+=1
}
// 没有查找到就返回false
return false
}
测试代码
let list = new LinkedList()
//2.插入数据
list.append('aaa')
list.append('bbb')
list.append('ccc')
/*---------------其他方法测试----------------*/
//remove方法
console.log(list.remove('aaa'));
console.log(list)
isEmpty()判断链表是否为空
代码
// 判断链表是否为空
LinkedList.prototype.isEmpty=function(){
return this.length==0
}
size()返回链表长度
代码
// 返回链表的长度
LinkedList.prototype.size=function(){
return this.length
}
测试代码
let list = new LinkedList()
//2.插入数据
list.append('aaa')
list.append('bbb')
list.append('ccc')
/*---------------其他方法测试----------------*/
//remove方法
console.log(list.isEmpty());
console.log(list.size())
单链表构造函数完整实现
// 封装链表的构造函数
function LinkedList() {
//封装一个Node类,用于保存每个节点信息
function Node(data) {
this.data = data
this.next = null
}
// 链表中的属性
this.length = 0 // 链表的长度
this.head = null //链表的第一个节点
//链表中的方法
// 1.追加节点的方法append,追加是指在链表的末尾添加节点
LinkedList.prototype.append = function (data) {
// 首先创建节点
let newNode = new Node(data)
// 然后找到末尾的节点,将新创建的节点添加到末尾
// 如果是空链,直接让头指针指向新节点
if (this.length == 0) {
this.head = newNode
} else {
// 从头开始查找,用current标记当前查找的位置
let current = this.head
// if(current==null) current=newNode // 也可以这样判断链表目前是否是空链
// 否则查找链表的最后一个节点
while (current.next) {
current = current.next
}
// 最后一个节点的current.next==null,所以会跳出while循环
// 让最后一个节点指向新节点
current.next = newNode
}
// 链表长度加一
this.length += 1
}
// 2.返回链表各个节点的内容的方法
LinkedList.prototype.toString = function () {
let current = this.head
let content = ''
// 空链表不会进入该循环,content为空
while (current) {
content += current.data + ' '// 每个节点数据后加个空格,便于阅读
current = current.next
}
return content
}
// position的有效范围是整数[0,length-1]
LinkedList.prototype.insert=function(position,data){
let newNode=new Node(data)
if(position<0|| position>this.length){
// false表示插入失败
return false;
}else if(position==0){//newNode成为头结点的情况
// 注意顺序不能颠倒
newNode.next=this.head
this.head=newNode
}else{
// 包含newNode成为最后一个节点的情况,与插入在中间位置一样的操作
let current=this.head
// 找到newNode要插入位置的前一个节点,跳出循环后current指向该节点
for(let i=0;i<position-1;i++){
current=current.next
}
// 顺序不能颠倒
newNode.next=current.next
current.next=newNode
}
this.length+=1
// true表示插入成功
return true
}
LinkedList.prototype.get=function(position){
// position有效取值是[0,this.length-1]间的整数
if(position<0|| position>=this.length) return null;
let current=this.head
let i=0
// 遍历至处于position位置的节点
while(i++<position){
current=current.next
}
// console.log(i); //position=2时,i=3,说明跳出循环i还是会自增1,因为自增运算符比比较运算符优先级高
// 跳出循环时,current已经指向处于position位置的节点
return current.data
}
// 根据数据查询数据所在链表位置
LinkedList.prototype.indexOf=function(data){
let current= this.head
let index=0
// 从头结点开始逐个查找数据等于data的节点
while(current){
if(current.data==data){
return index
}
current=current.next
index+=1
}
// 没有查找到就返回-1
return -1
}
LinkedList.prototype.update=function(position,newData){
// position有效取值是[0,this.length-1]间的整数,修改失败返回false
if(position<0|| position>=this.length) return false;
let current=this.head
let i=0
// 遍历至处于position位置的节点
while(i++<position){
current=current.next
}
// console.log(i); //position=2时,i=3,说明跳出循环i还是会自增1,因为自增运算符比比较运算符优先级高
// 跳出循环时,current已经指向处于position位置的节点
current.data=newData
return true
}
LinkedList.prototype.removeAt=function(position){
// 超出范围的删除不了
if(position<0|| position>=this.length) return false;
let current =this.head
// 如果删除第一个节点
if(position==0){
// 在JS中,垃圾回收机制会清理未被指向的对象
this.head=this.head.next
}else{
let i=0;
let previous=this.head
while(i++<position){
previous=current
current=current.next
}
// 在JS中,垃圾回收机制会清理未被指向的对象
previous.next=current.next
}
this.length--;
return current.data
}
LinkedList.prototype.remove=function(data){
let current= this.head
let index=0
let previous=this.head
// 从头结点开始逐个查找数据等于data的节点
while(current){
if(current.data==data){
// 如果删除的是头节点
if(index==0){
this.head=this.head.next
}else{
previous.next=current.next
}
this.length--;
return index
}
// previous和current指向下一个节点
previous=current
current=current.next
index+=1
}
// 没有查找到就返回false
return false
}
// 判断链表是否为空
LinkedList.prototype.isEmpty=function(){
return this.length==0
}
// 返回链表的长度
LinkedList.prototype.size=function(){
return this.length
}
}
链表节点实现
Java
// Definition for singly-linked list.
public class SinglyListNode {
int val;
SinglyListNode next;
SinglyListNode(int x) { val = x; }
}
C++
// Definition for singly-linked list.
struct SinglyListNode {
int val;
SinglyListNode *next;
SinglyListNode(int x) : val(x), next(NULL) {}
};
JS
//封装一个Node类,用于保存每个节点信息
function Node(element){
this.element=element
this.next=null
}
经典相关算法题
链表反转
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表
示例 1:

示例2

示例3
空链表反转后仍为空
题解
- 遍历节点,将每个节点的指向反转
/**
* 定义单链表节点
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function(head) {
// cur指向当前遍历的节点,pre指向前一个节点,
let next=undefined,pre=null,cur=head;
while(cur){
// 顺序不能颠倒
// next存储当前遍历节点的下一个结点的引用
next=cur.next
// 反转指向
cur.next=pre
// pre指向后移一位
pre=cur;
// cur指向后移一位
cur=next
}
// 最终的pre成为新的头指针
head=pre
return head
};
复杂度分析
时间复杂度:O(n),其中 n 是链表的长度。需要遍历链表一次。
空间复杂度:O(1)
- 递归
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function(head) {
let pre=head,cur=head.next;
// 考虑空链表和只有一个节点的情况
if(pre==null || cur==null){
head.next=null
return pre
};
cur.next=pre
return reverseList(cur)// 此时cur就相当于head
};
数组
- 查找时间复杂度:O(1),因为可以直接根据索引查找
- 插入或删除时间复杂度O(n),因为要移动删除或插入位置后面的数组元素
哈希表/散列表
用哈希函数确定键的存储位置
特点
树
因为所有树都可以转换成二叉树的形式,所以这里就只介绍二叉树数据结构的实现方式
完美二叉树(Perfect Binary Tree)/满二叉树(Full Binary Tree)
完全二叉树(Compelete Binary Tree)
二叉搜索树/二叉查找树/二叉排序树(Binary Search Tree,简称BST)
二叉搜索树构造函数实现如下
function BinarySearchTree(){
this.root=null
// 节点构造函数
function Node(key){
this.key=key
this.left=null
this.right=null
}
}
二叉搜索树的常见操作:
insert(key):向树中插入一个新的键;
search(key):在树中查找一个键,如果节点存在,则返回true;如果不存在,则返回false;
inOrderTraverse:通过中序遍历方式遍历所有节点;
preOrderTraverse:通过先序遍历方式遍历所有节点;
postOrderTraverse:通过后序遍历方式遍历所有节点;
min:返回树中最小的值/键;
max:返回树中最大的值/键;
remove(key):从树中移除某个键;
按照这个算法,在相同的顺序下最终所形成的二叉搜索树应该是一样的