【排序算法】图解简单选择排序(图解堪比Debug显示每次循环结果)
【排序算法】图解简单选择排序(图解堪比Debug分析每次循环结果)
写在前面：
本文主要介绍简单选择排序算法，通过图片一步步解释每一趟每一次的后移。代码通过C#实现，并输出每一次交换的情况和比较次数，方便各位小伙伴比较算法的优缺点。图解堪比Debug，一步步分析每次循环结果。
活动地址：CSDN21天学习挑战赛
本文关键字：经典算法、排序算法、选择排序、简单选择排序、图解、C#
文章目录
- 【排序算法】图解简单选择排序(图解堪比Debug分析每次循环结果)
-
-
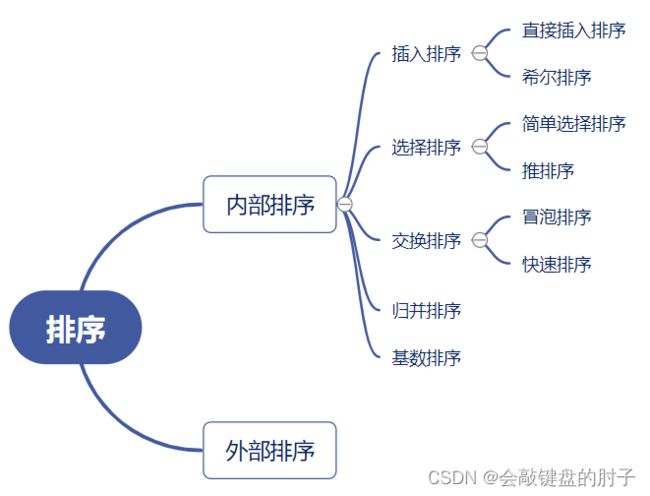
- 一、排序算法分类
- 二、算法效率
-
- 1. 时间复杂度
- 2. 空间复杂度
- 三、选择排序
-
- 1. 简单选择排序
- 2. 推排序
- 六、算法实践
-
- 1. 图解算法原理
- 2. 算法实现
- 3.时间复杂度
- 4.空间复杂度
-
一、排序算法分类
-
内部排序
指将需要处理的所有数据都加载到内部存储器（内存）中进行排序。
-
外部排序
数据量过大，无法全部加载到内存中，需要借助外部存储（文件等）进行排序。
-
常见的分类方法
二、算法效率
1. 时间复杂度
度量一个程序（算法）执行时间的两种方法。
-
事后统计的方法
这种方法可行，但有两个问题：一是要想对设计的算法的运行性能进行评测，需要事件运行该程序；二是所得时间的统计量依赖于计算机的硬件、软件等环境因素。
-
事前估算的方法
通过分析某个算法的时间复杂度来判断哪个算法更优。
-
时间频度
一个算法花费的时间与算法中语句的执行次数成正比。一个算法中的语句执行次数称为语句频度或者时间频度。记为T(n)。
此处引用清华大学《数据结构》课程的一段话，一般情况下，算法中的基本操作语句的重复执行次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作 T(n)=Ｏ( f(n) )，称Ｏ( f(n) ) 为算法的渐进时间复杂度，简称时间复杂度。
2. 空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元。
三、选择排序
每一趟从无序区中选出关键字最小的元素，按顺序放在有序区的最后（生成新的有序区，无序区元素个数减1），直到全部排完为止。
1. 简单选择排序
也称直接选择排序 Select Sorting，整个过程就是每一趟都将无序区中的所有元素进行逐一比较，找到最小的元素，与无序区中的首个元素进行交换，有序区长度加1，无序区长度减1。重复以上步骤，直到所有的元素均已排好。
2. 推排序
堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。
堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆, 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。
六、算法实践
1. 图解算法原理
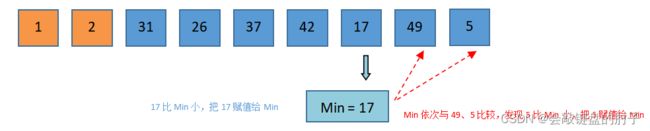
第一次从arr[0]~arr[n-1]中选取最小值，与arr[0]交换，第二次从arr[1]~arr[n-1]中选取最小值，与arr[1]交换，第三次从arr[2]~arr[n-1]中选取最小值，与arr[2]交换，…，第i次从arr[i-1]~arr[n-1]中选取最小值，与arr[i-1]交换，…, 第n-1次从arr[n-2]~arr[n-1]中选取最小值，与arr[n-2]交换，总共通过n-1次，得到一个按排序码从小到大排列的有序序列。
下面通过一个动图来看一看直接选择排序到底是怎么样移动的。
那么，具体是如何移动的，我们以上面动图的数组[5, 42, 31, 26, 37, 2, 17, 49, 1]为例。
假设我们有数组[5, 42, 31, 26, 37, 2, 17, 49, 1]，要求按升序排列。
图解约定
- 橙色矩形块表示有序区
- 红色虚线箭头表示两数比较
- 橙色实线箭头表示交换
- 蓝色箭头表示构造一个临时变量并赋值
- 我们假设
arr = [5, 42, 31, 26, 37, 2, 17, 49, 1]，临时变量Min=0
-
第
i = 0趟
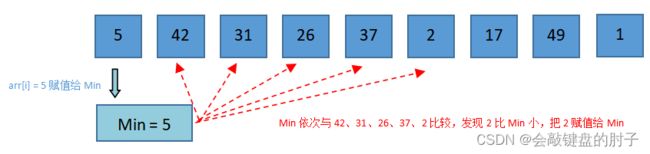
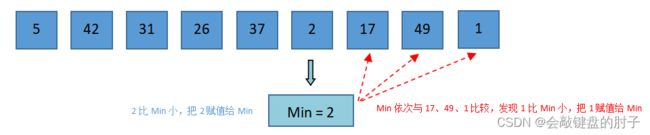
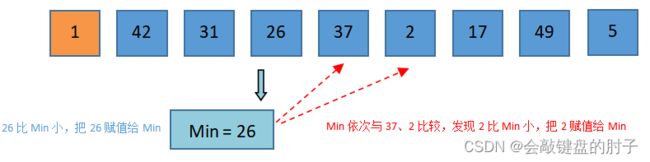
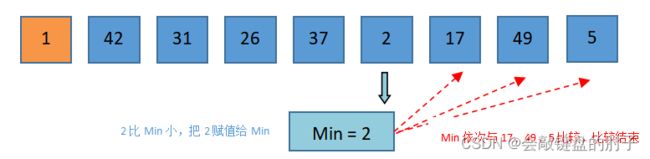
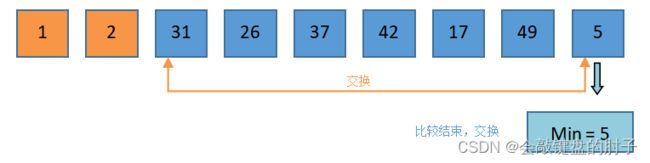
将arr[i] = 5赋值给Min，并将Min依次与42、31、26、37、2比较，发现2比Min小。此时，Min需要重置，把2赋值给Min。- 第1次重置
将2赋值给
Min，Min依次与17、49、1比较，发现1比Min小。此时，Min需要重置，把1赋值给Min。- 第2次重置
此时，比较结束，将
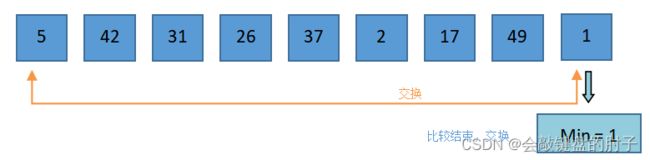
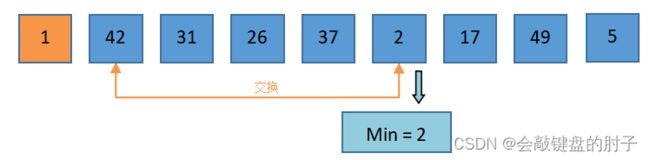
Min与arr[0]交换，即1和5交换。 - 第1次重置
-
第
i = 1趟
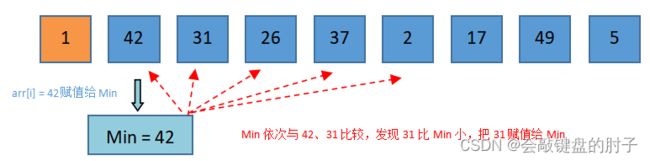
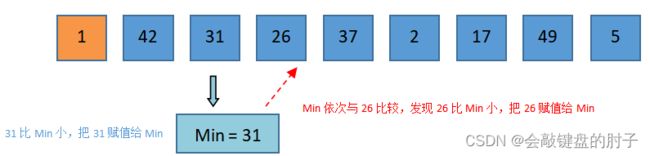
将arr[i] = 42赋值给Min，并将Min依次与42、31比较，发现31比Min小。此时，Min需要重置，把31赋值给Min。- 第1次重置
将31赋值给
Min，Min依次与26比较，发现26比Min小。此时，Min需要重置，把26赋值给Min。- 第2次重置
将26赋值给
Min，Min依次与37、2比较，发现2比Min小。此时，Min需要重置，把2赋值给Min。- 第3次重置
将2赋值给
Min，Min依次与17、49、5比较。此时，比较结束，将Min与arr[1]交换，即2和42交换。
- 第1次重置
-
第
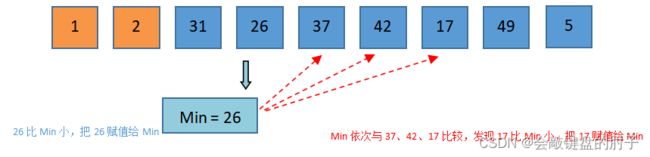
i = 2趟
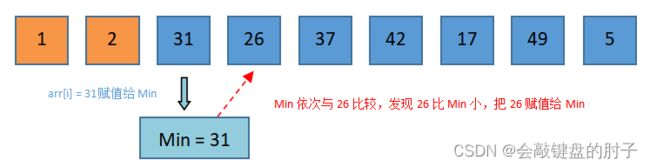
将arr[i] = 31赋值给Min，Min依次与26比较，发现26比Min小。此时，Min需要重置，把26赋值给Min。- 第1次重置
将26赋值给
Min，Min依次与37、42、17比较，发现17比Min小。此时，Min需要重置，把17赋值给Min。- 第2次重置
将17赋值给
Min，Min依次与49、5比较，发现5比Min小。此时，Min需要重置，把5赋值给Min。- 第3次重置
将5赋值给
Min，此时，比较结束，将Min与arr[2]交换，即5和31交换。 - 第1次重置
后面步骤也很简单，不再给出，有需要的小伙伴可以关注博主，向博主索要。
2. 算法实现
///
/// 直接选择排序静态类
///
public static class SelectSort
{
public static void SelectSortMethod(int[] arr)
{
//选择排序时间复杂度是 O(n^2)
for (int i = 0; i < arr.Length - 1; i++)
{
Console.WriteLine($"==============第{i+1}趟排序==============");
int minIndex = i;
int min = arr[i];
int count = 0;
for (int j = i + 1; j < arr.Length; j++)
{
if (min > arr[j])
{ // 说明假定的最小值，并不是最小
min = arr[j]; // 重置min
minIndex = j; // 重置minIndex
count++;
Console.WriteLine("第" + count + "次重置后数组：");
Console.WriteLine(string.Join(" ", arr));
Console.WriteLine("第" + count + "次重置后Min：");
Console.WriteLine(min);
}
}
// 将最小值，放在arr[0], 即交换
if (minIndex != i)
{
arr[minIndex] = arr[i];
arr[i] = min;
}
Console.WriteLine($"第{i+1}趟排序后数组：");
Console.WriteLine(string.Join(" ",arr));
}
}
}
class Program
{
static void Main(string[] args)
{
//测试直接选择排序
int[] intArray = new int[] { 5, 42, 31, 26, 37, 2, 17, 49, 1 };
SelectSort.SelectSortMethod(intArray);
}
}
==============运行结果===============
==============第1趟排序==============
第1次重置后数组：
5 42 31 26 37 2 17 49 1
第1次重置后Min：
2
第2次重置后数组：
5 42 31 26 37 2 17 49 1
第2次重置后Min：
1
第1趟排序后数组：
1 42 31 26 37 2 17 49 5
==============第2趟排序==============
第1次重置后数组：
1 42 31 26 37 2 17 49 5
第1次重置后Min：
31
第2次重置后数组：
1 42 31 26 37 2 17 49 5
第2次重置后Min：
26
第3次重置后数组：
1 42 31 26 37 2 17 49 5
第3次重置后Min：
2
第2趟排序后数组：
1 2 31 26 37 42 17 49 5
==============第3趟排序==============
第1次重置后数组：
1 2 31 26 37 42 17 49 5
第1次重置后Min：
26
第2次重置后数组：
1 2 31 26 37 42 17 49 5
第2次重置后Min：
17
第3次重置后数组：
1 2 31 26 37 42 17 49 5
第3次重置后Min：
5
第3趟排序后数组：
1 2 5 26 37 42 17 49 31
==============第4趟排序==============
第1次重置后数组：
1 2 5 26 37 42 17 49 31
第1次重置后Min：
17
第4趟排序后数组：
1 2 5 17 37 42 26 49 31
==============第5趟排序==============
第1次重置后数组：
1 2 5 17 37 42 26 49 31
第1次重置后Min：
26
第5趟排序后数组：
1 2 5 17 26 42 37 49 31
==============第6趟排序==============
第1次重置后数组：
1 2 5 17 26 42 37 49 31
第1次重置后Min：
37
第2次重置后数组：
1 2 5 17 26 42 37 49 31
第2次重置后Min：
31
第6趟排序后数组：
1 2 5 17 26 31 37 49 42
==============第7趟排序==============
第7趟排序后数组：
1 2 5 17 26 31 37 49 42
==============第8趟排序==============
第1次重置后数组：
1 2 5 17 26 31 37 49 42
第1次重置后Min：
42
第8趟排序后数组：
1 2 5 17 26 31 37 42 49
总结
- 这里我们假设数组
[5, 42, 31, 26, 37, 2, 17, 49, 1]为变量arr。- 从以上过程可得，直接选择排序算法是遍历一次所有数，但最后一个数不用排，因此n个数需要n-1次遍历，即i直接从0开始，即
for(int i = 0; i < arr.Length - 1; i++)。- 我们创建一个临时变量
Min和MinIndex，分别记录最小值和其索引。- 每一次Min的比较都是从后一个数开始，所以我们可以直接将第二个循环的参数j设为i-1，即
for (int j = i + 1; j < arr.Length; j++)。- 然后比较，如果Min并不是最小值即
min > arr[j]，就重置Min和MinIndex，即min = arr[j]和minIndex = j。- 比较完之后，循环结束，我们将
Min和arr[i]交换，即arr[i] = min和arr[minIndex] = arr[i]。- 另外，当出现Min没有被重置时，不需要交换，即
if (minIndex != i)时才执行交换。
我们通过运行结果可以看出，输出的结果与我们图解分析的内容是一致，并且我们可以发现每趟只交换一次，每趟过程中数组没有发生变化，这也是选择排序和冒泡排序的不同之处，冒泡排序一趟会比较至少一次，所以我们所选择排序在性能上优于冒泡排序。
3.时间复杂度
若数组是正序的，一趟即可完成排序。最好的时间复杂度为 O(n)。
若数组反序，如果是 n 个数字，那么就是
( n − 1 ) + ( n − 2 ) + . . . + 2 + 1 = n ( n − 1 ) / 2 = n 2 / 2 − n / 2 (n-1)+(n-2)+...+2+1 = n(n-1)/2 = n^2/2 - n/2 (n−1)+(n−2)+...+2+1=n(n−1)/2=n2/2−n/2
根据复杂度的规则，去掉低阶项和常数系数，那复杂度就是 **O(n^2)**了。
4.空间复杂度
算法执行过程中，只需要一个临时变量来进行存储插入值，所以空间复杂度是O(1)。
写在结尾：
文章中出现的任何错误请大家批评指出，一定及时修改。
希望看到这里的小伙伴能给个三连支持！