【洛谷1661 扩散】二分答案 | 并查集 | 最小生成树 | E

谨以此题纪念我的第一次正式二分答案~

洛谷【P1661】 扩散

时空限制 1000ms / 128MB 698通过 1.7K提交

Tags： 二分答案 最小生成树 并查集

题目描述

一个点每过一个单位时间就会向四个方向扩散一个距离，如图。

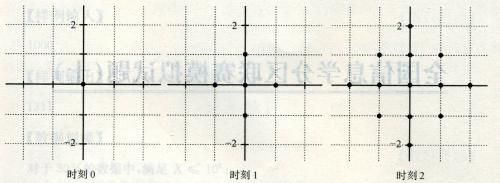
给出多个点的坐标，每个点会扩散成一个块，求所有的块连通的最早时刻。

注意，不一定需要每两个块都直接导通。只要大家都融在一起了就行。另外，连通必须重合，邻接是不行的。具体见样例就明白了。

输入

$1$ 组。第一行一个数 $N$，接下来 $N$ 行，每行一个点坐标 $X[i]和Y[i]$

对于 $20\%$ 的数据，满足 $1\le N\le 5$; $1\le X[i],Y[i]\le 50$;

对于 $100\%$ 的数据，满足 $1\le N\le 50$; $1\le X[i],Y[i]\le 10^9$。

输出

输出一个数，表示所有的块连通的最早时刻。

输入样例 1

2
0 0
1 2

输出样例 1

2

输入样例 2

2
0 0
5 5

输出样例 2

5

分析

此题最直接想到的应该是建最小生成树然后求里面的最长边就找到了答案。不过也可以二分答案找满足条件的最小距离。

当然不管怎么做，都得事先求一遍每两个点间的曼哈顿距离。不妨拿邻接矩阵来存。

首先分析最小生成树解法：

• 相当稠密的图，所以用Prim算法会比较合算。
• 该算法从任选一个点开始，然后循环找未收录的、离生成树最近的的邻接点加进生成树，并尝试更新它的邻接点到当前生成树的距离。
• 循环持续到找不到未收录的最近邻接点为止。找到 $V$ 个点后就建出了最小生成树。否则找不到（图不连通）。
• 当然本题要找的就是最小生成树里面的最长边，所以建树的时候顺便更新最大值就行。
• 整个过程的时间复杂度很显而易见，建图 $\Theta (V^2)$ + $Prim$ $O(V^2)$。空间复杂度 $\Theta (V^2)$。
  - 不必用堆优化。这里边数是 $\Theta (V^2)$ 的，堆优化后复杂度是 $O((V+E)\log V)$，即 $O(V^2\log V)$，显然不合算嘛。
  
  
  

然后分析二分答案解法：（还需用到并查集）

• 目标：找可行的最短时间（实际上是找可行的最短扩散距离）
• 单调性：这里当然满足单调性啦 ~ 当一个距离满足要求的时候，比它大的肯定更满足；比它小的可能不满足所以我们要尝试再减小。因为是要找尽量小的解，所以最后二分出的答案是是L而不是R。
• 初始上下界：分别是任意两对点间最长/最短的曼哈顿距离。
• 检验函数：为了检查一个 $ANS$，需要把所有距离 $\le ANS$ 的点对都用并查集连起来。遍历完成后，如果所有点都在同一个集合中，则该解是可行的。
• 复杂度：使用按规模归并 + 路径压缩的并查集，两个操作均摊复杂度均可以认为是为 $O(1)$。故检验函数复杂度 $\Theta (V^2)$。
• 复杂度：最大二分范围记为 $M$，则整体时间复杂度 $O(V^2{\log }_{2}M)$，最坏不超过 $10^5$，很$ok$。空间复杂度 $\Theta (V^2)$
  
  
  
  

AC代码

首先是最小生成树解法的代码：

#include <cstdio>
#include <cmath>
#include <cstring>

#define sc(x) {register char _c=getchar(),_v=1;for(x=0;_c<48||_c>57;_c=getchar())if(_c==45)_v=-1;for(;_c>=48&&_c<=57;x=(x<<1)+(x<<3)+_c-48,_c=getchar());x*=_v;}
#define PC putchar
#define M_DIST(u, v) (x[u]>x[v]?x[u]-x[v]:x[v]-x[u])+(y[u]>y[v]?y[u]-y[v]:y[v]-y[u])
template<typename T>void UPRT(const T a){if(a>=10)UPRT(a/10);PC(a%10+48);}

constexpr int MN(52);

int x[MN], y[MN];
int V, g[MN][MN];
int ds[MN];

int prim(const int SRC)
{
	int max_min_d = -1;
	for (int v=0; v<V; ++v)
		ds[v] = g[SRC][v];

	while (1)
	{
		int u = -1, min_d = 2e9+2333;
		for (int v=1; v<V; ++v)
			if (ds[v] && min_d > ds[v])
				min_d = ds[u = v];
		if (~u)
		{
			ds[u] = 0;
			if (max_min_d < min_d)
				max_min_d = min_d;
			for (int v=1; v<V; ++v)
				if (ds[v] && ds[v] > g[u][v])
					ds[v] = g[u][v];
		}
		else break;
	}
	return max_min_d;
}

int main()
{
	sc(V)
	if (V == 1)
		return PC('0'), 0;

	for (int u=0; u<V; ++u)
	{
		sc(x[u])sc(y[u])
		for (int v=0; v<u; ++v)
			g[u][v] = g[v][u] = M_DIST(u, v);
	}

	int max_min_d = prim(0);
	UPRT( (max_min_d+1) / 2 );
}

然后是二分答案 + 并查集解法的代码：

#include <cstdio>
#include <cstring>

#define sc(x) {register char _c=getchar(),_v=1;for(x=0;_c<48||_c>57;_c=getchar())if(_c==45)_v=-1;for(;_c>=48&&_c<=57;x=(x<<1)+(x<<3)+_c-48,_c=getchar());x*=_v;}
#define PC putchar
#define M_DIST(u, v) (x[u]>x[v]?x[u]-x[v]:x[v]-x[u])+(y[u]>y[v]?y[u]-y[v]:y[v]-y[u])
template<typename T>void UPRT(const T a){if(a>=10)UPRT(a/10);PC(a%10+48);}

constexpr int MN(52);

bool vis[MN];
int V, x[MN], y[MN];

template <const int MN>
class UF
{
	public:

		int uf[MN];

	public:

		UF(void) { }

		inline void init(int V)
		{
			memset(uf, -1, (V+1) * sizeof(*uf));
		}

		int find(int x)
		{
			if (uf[x] >= 0)
				uf[x] = find(uf[x]);
			return uf[x];
		}

		void merge(int x, int y)
		{
			int r1 = find(x);
			int r2 = find(y);
			if (r1<r2)
			{
				uf[r1] += uf[r2];
				uf[r2] =  r1;
			}
			else if(r2<r1)
			{
				uf[r2] += uf[r1];
				uf[r1] =  r2;
			}
		}

		bool connected(int x, int y)
		{
			return find(x) == find(y);
		}
};

UF<MN> uf;

bool check(const int ANS)
{
    uf.init(V);
    for (int u=0; u<V; ++u)
        for (int v=0; v<V; ++v)
            if (M_DIST(u, v) <= ANS)
                uf.merge(u, v);
    const int ROOT = uf.find(0);
    for (int u=0; u<V; ++u)
        if (uf.find(u) != ROOT)
            return false;
    return true;  
}

int binbin(int L, int R)
{
    while (L <= R)
    {
        int mid = L + (R-L)/2;
        if (check(mid))
            R = mid-1;
        else
            L = mid+1;
    }
    return L;
}

int main()
{
    sc(V)
    if (V == 1)
        return PC('0'), 0;

    for (int u=0; u<V; ++u)
    {
        sc(x[u])sc(y[u])
    }

    int max_min_d= binbin(1, 1e9);
    UPRT( (max_min_d+1) / 2 );
}

加油！