《数字图像处理》第四章 频率域滤波 学习笔记附部分例子代码(C++ & opencv)

0. 前言

本章节算是一大重点，所以本文的代码写的详细一些，希望大家共同进步。如发现任何问题，希望能在评论区友好交流。

第三版教材中图片下载地址： book images downloads

vs2019配置opencv可以查看：VS2019 & Opencv4.5.4配置教程

前情回顾：
数字图像处理第三章 学习笔记

后续剧情：
数字图像处理第六章 彩色图像处理 学习笔记
数字图像处理第七章 小波域多分辨率处理 学习笔记
数字图像处理 第九章 形态学图像处理 学习笔记
数字图像处理 第十章 图像分割 学习笔记
数字图像处理 第11章 表示和描述 学习笔记

1. 基本概念

这一小节主要是复习了复数和傅里叶变换, 包括离散变量和连续变量. 笔记不详细写了.

傅里叶变换对:

• $F(\mu )={\int }_{-\infty }^{\infty }f(t){\mathrm{e}}^{-\mathrm{j}2\pi \mu t}\mathrm{d}t$

• $f(t)={\int }_{-\infty }^{\infty }F(\mu ){\mathrm{e}}^{\mathbf{j}2\pi \mu t}\mathrm{d}\mu$

根据欧拉公式, ${\mathrm{e}}^{\mathbf{j}2\pi \mu t}=\cos (2\pi \mu t)-j\sin (2\pi \mu t)$, 傅里叶变换正弦项的频率由$\mu$决定, 积分后左边剩下的唯一变量是频率, 故我们说傅里叶变换域为频率域.

1.1 取样函数的傅里叶变换

空间域俩个函数的乘积的傅里叶变换是两个函数在频率域的卷积

$$\mathcal{F}\{f(t)s_{\Delta T}(t)\}=F(\mu )★S(\mu )=\frac{1}{\Delta T}\sum _{n=-\infty }^{\infty }F\left(\mu -\frac{n}{\Delta T}\right)$$

取样定理: 取样率$1/2\Delta T$要大于${\mu }_{max}$这一最大频率, 这样才能复原信号.

混淆: 实践中, 混淆是无可避免的事, 可以通过平滑输入函数以减少高频分量来降低混淆的影响

1.2 单变量的离散傅里叶变换(DFT)

本节为二维变量DFT的基础

$$\begin{gathered} F(u)=\sum _{x=0}^{M-1}f(x){\mathrm{e}}^{-j2\pi ux/M},\mu =0,1,2,\cdot \cdot \cdot ,M-1 \\ f(x)=\frac{1}{M}\sum _{u=0}^{M-1}F(u){\mathrm{e}}^{j2\pi u\mathrm{x}/M},x=0,1,2,\cdot \cdot \cdot ,M-1 \end{gathered}$$

其中$u$表示频率变量, x表示采样的距离(图像的横坐标)

取样和频率间隔的关系:

• DFT的频率分辨率$\Delta u$取决于连续函数$f(t)$被取样的持续时间T

• DFT跨越的频率的范围取决于取样间隔$\Delta T$

盒装滤波器: 所有系数都相等的空间均值滤波器

2. 两个变量函数的扩展

二维离散傅里叶变换本质就是矩阵的运算, 理解了单变量, 二维就很好理解了，如理解困难，可所有搜索相关视频教程。

公式如下

$$F(u,\nu )=\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}f(x,y){\mathrm{e}}^{-\mathrm{j}2\pi (ux/M+vy/\mathrm{N})}$$

3. 二维傅里叶变换的一些性质

3.1 傅里叶谱

幅度: $|F(u,\nu )|={\left[R^2(u,\nu )+I^2(u,\nu )\right]}^{1/2}$

功率谱: $F(u,v)={\left|F(u,v)\right|}^2=R^2(u,v)+I^2(u,v)$

又 ∣ F ( 0 , 0 ) ∣ = M N ∣ f ‾ ( x , y ) ∣ \left|F(0,0)\right|=M N\left|{\overline{{f}}}(x,y)\right| ∣F(0,0)∣=MN ​f​(x,y) ​, 所以(0, 0)处是谱的最大分量, 可能比其他项大几个数量级, 所以在查看图像谱时, 会对谱进行一次对数变换(见第二章2.2).

Mat fourierTransform(Mat input) {
    input.convertTo(input, CV_32F);

    Mat fourierRes;
    // 进行二维傅里叶变换
    // planes第一个元素对input进行深拷贝,作为实部, 第二个元素创建同样大小的零矩阵
    Mat planes[2] = {Mat_<float>(input), Mat::zeros(input.size(), CV_32F) };
    merge(planes, 2, fourierRes);
    dft(fourierRes, fourierRes, DFT_COMPLEX_OUTPUT);
    split(fourierRes, planes);

    //使用magnitude函数求幅度谱
    Mat magnitudeRes;
    magnitude(planes[0], planes[1], magnitudeRes);
    normalize(magnitudeRes, magnitudeRes, 0, 1, NORM_MINMAX);
    //imshow("幅度谱", magnitudeRes);

    //进行中心化
    int centerX = magnitudeRes.rows / 2;
    int centerY = magnitudeRes.cols / 2;
    Mat q1(magnitudeRes, Rect(0, 0, centerX, centerY));
    Mat q2(magnitudeRes, Rect(centerX, 0, centerX, centerY));
    Mat q3(magnitudeRes, Rect(0, centerY, centerX, centerY));
    Mat q4(magnitudeRes, Rect(centerX, centerY, centerX, centerY));

    //交换象限
    Mat tmp;
    q1.copyTo(tmp);
    q4.copyTo(q1);
    tmp.copyTo(q4);

    q2.copyTo(tmp);
    q3.copyTo(q2);
    tmp.copyTo(q3);
    //magnitudeRes.convertTo(magnitudeRes, CV_8U);
    imshow("centralization", magnitudeRes);
    // 试验发现, 这里要将中心化结果保存位深为8的png照片, 再读取之后进行对数变换
    // 这样做, 才能显示"正常"的图片, 目前不知道是什么理由, 可能跟tif格式有关.
    normalize(magnitudeRes, magnitudeRes, 0, 255, NORM_MINMAX);
    //imshow("centralization", magnitude)    //此时show出来的图片样式不对.
    imwrite("centralization.png", magnitudeRes);    
}
// 右俩图由下面代码得到.(折磨了我好久)
Mat img = imread("centralization.png", IMREAD_GRAYSCALE);
imshow("中心化结果", img);
img.convertTo(img, CV_32F);

Mat logg;
log(1.0 + img, logg);

normalize(logg, logg, 0, 255, NORM_MINMAX);
logg.convertTo(logg, CV_8U);
imshow("对数变换", logg);
waitKey(0);

3.2 相角

$$\varphi (u,\nu )=\arctan \left[\frac{I(u,\nu )}{R(u,\nu )}\right]$$

称为相角

//通过原图和实虚部获得相位谱
Mat getPhaseSpec(Mat input, Mat* planes) {
    input.convertTo(input, CV_32F);

    Mat fourierRes;
    // 进行二维傅里叶变换
    merge(planes, 2, fourierRes);
    dft(fourierRes, fourierRes, DFT_SCALE | DFT_COMPLEX_OUTPUT);
    split(fourierRes, planes);

    //通过实虚部获得相位谱
    Mat phaseImg;
    phase(planes[0], planes[1], phaseImg);

    return phaseImg;
}
//通过相位谱重构图像
Mat phaseToImg(Mat phase, Mat* planes) {
    Mat result;
    //polarToCart: 将极坐标形式的输入转换为直角坐标形式
    //构建一个复数图像, 实部为1, 虚部为相位谱
    polarToCart(Mat::ones(phase.size(), phase.type()), phase, planes[0], planes[1]);
    merge(planes, 2, result);
    idft(result, result, cv::DFT_SCALE | cv::DFT_REAL_OUTPUT);
    //归一化
    cv::normalize(result, result, 0, 255, cv::NORM_MINMAX);
    result.convertTo(result, CV_8U);

    return result;
}

void test01(string path) {
    Mat img = imread(path, IMREAD_GRAYSCALE);
    if (img.empty()) {
        cerr << "Error: unable to load the image\n";
        return;
    }
    // planes第一个元素对input进行深拷贝,作为实部, 第二个元素创建同样大小的零矩阵
    Mat planes[2] = { Mat_<float>(img), Mat::zeros(img.size(), CV_32F) };
    Mat phase = getPhaseSpec(img, planes);
    Mat reconImg = phaseToImg(phase, planes);

    imshow("原图", img);
    imshow("相位谱", phase);
    imshow("相角重构图像", reconImg);
    waitKey(0);
}

3.3 二维卷积定理

二维卷积定理的表达式:

$$f(x,y)\star h(x,y)⟺F(u,y)H(u,v)$$

注意: 如果卷积的俩个函数为周期函数, 为了解决纠缠错误, 我们需要对函数进行补0, 使他们有相同的大小. 令填充后的图像大小为$P\times Q$, 其中

$$\begin{array}{c}P\ge A+C-1\\ Q\ge B+D-1\end{array}$$

A, B分别为f(x, y)的宽, 高; C, D分别为h(x, y)的宽高.

4. 频率滤波基础

4.1 基础

频率域滤波: 修改一幅图像的傅里叶变换然后计算其反变换得到处理后的结果.

低通滤波器将模糊一幅图像, 而高通滤波器将增强尖锐的细节. 对滤波器加上一个小常数不会影响尖锐性, 并且保留色调.

等同地影响实部和虚部而不影响相位的滤波器称为零相移滤波器.

4.2 频率域滤波步骤

1. 填充图像为(P, Q), P=2M, Q=2N.

// 第一步:填充. 填充俩倍
Mat getPaddedImg(Mat input) {
    int nCols = input.cols;
    int nRows = input.rows;
    // 规则：Size(宽， 高)
    Mat result = Mat::zeros(Size(2 * nCols, 2 * nRows), input.type());
    input.copyTo(result(Range(0, nCols), Range(0, nRows)));
    return result;
}

2. 图像乘$(-1{)}^{x+y}$使频率谱中心化(代替了3.1中复杂的中心化步骤了).

3. 计算DFT

Mat getSpectrum(Mat input) {
    int nRows = input.rows;
    int nCols = input.cols;
    Mat dftRes;
    input.convertTo(input, CV_32F);
    //Mat_ powerMat(nRows, nCols);
    for (int x = 0; x < nRows; x++) {
        for (int y = 0; y < nCols; y++) {
            input.at<float>(x, y) *= pow(-1, x + y);
        }
    }
    imshow("fp", input);
    dft(input, dftRes, DFT_SCALE | DFT_COMPLEX_OUTPUT);
    //此时的输出是复数形式.
    return dftRes;
}

4. 生成需要的滤波器, 与DFT结果相乘(相乘的操作见主测试函数), 高斯低通滤波器二维表达式如下:

   • $$H(u,v)={\mathrm{e}}^{-D^2(u,v)/2D_0}$$

   • 其中D(u, v)表示距离中心的距离, D0表示截止频率, 就是下面的sigma的大小.

Mat generateGLPF(int size, double sigma) {
    // 计算滤波器中心
    int centerX = size / 2;
    int centerY = size / 2; 
    // CV_64FC2的解释见 "opencv补充"第二点
    Mat filter(size, size, CV_64FC2);
    for(int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            double distance = sqrt((i - centerX) * (i - centerX) + (j - centerY) * (j - centerY));
            double value = exp(-0.5 * (distance * distance) / (sigma * sigma));
            filter.at<Vec2d>(i, j) = Vec2d(value, 0);
        }
    }
    return filter;
}

5. 逆变换得到处理后的图像.

Mat idftImg(Mat complex) {
    Mat result;
    // 让输出为实数
    idft(complex, result, DFT_REAL_OUTPUT);
    for (int x = 0; x < result.rows; x++) {
        for (int y = 0; y < result.cols; y++) {
            result.at<double>(x, y) *= pow(-1, x + y);
        }
    }
    return result;
}

主测试函数如下:

// 测试频率域滤波全过程
void test(string path) {
    Mat img = imread(path, IMREAD_GRAYSCALE);
    if (img.empty()) {
        cerr << "Error: unable to load the image\n";
        return;
    }
    resize(img, img, Size(256, 256));    //原图片太大了
    Mat paddedRes = getPaddedImg(img);
    Mat dftRes = getSpectrum(paddedRes);
    Mat filter = generateGLPF(2 * img.rows, 20);
    //---------------------频谱相乘------------------------
    Mat filteredSpec;
    dftRes.convertTo(dftRes, CV_64F);
    assert(dftRes.type() == filter.type());
    //mulSpectrums函数中, 俩个数据的类型必须一致!!!!!!
    mulSpectrums(dftRes, filter, filteredSpec, 0);
    //----------------------------------------------------
    Mat idftRes = idftImg(filteredSpec);

    imshow("原图", img);
    imshow("填充的结果", paddedRes);
    displayComplexImg(dftRes, "频谱");//这个函数我贴在6.1了, 很简单, 将实部虚部拆开, 然后求平方根.   
    displayComplexImg(filter, "滤波器频谱");
    displayComplexImg(filteredSpec, "相乘之后的频谱");
    //cout << filteredSpec.type() << endl;
    imshow("逆变换结果", idftRes);
    imshow("图h", idftRes(Rect(0, 0, img.rows, img.rows)));
    waitKey(0);
}

图c和图d与书本区别很大(折磨了很久还是没找到是啥问题~)

4.3 空间和频率域滤波间的对应

空间域与频率域的滤波器形成的傅里叶变换对:

$$h(x,y)⟺H(u,v)$$

其中, h(x, y)是一个空间滤波器-----有限冲激响应(FIR)滤波器, 而H(u, v)又可以被称为脉冲响应.

5. 使用频率域滤波器平滑图像

这其中原理与以上很类似, 只需要改变滤波器即可(套公式), 不做过多实验了.

• 理想低通滤波器(ILPF):

• 布特沃斯低通滤波器(BLPF): 在截止频率点, H(u, v)下降50%

• 高斯低通滤波器(GLPF): 振铃效果得到很好抑制

6. 使用频率域滤波器锐化图像

6.1 高斯高通滤波器

这里还是再做一下吧, 下面把频谱相乘也模块化了(写成了一个函数), 同时优化了显示的函数.(不断试验发现的, 使用imshow之前最好要归一化为CV_8U 数据类型)

//生成高斯高通滤波器很简单, 1-低通即可
Mat generateGHPF(int size, double sigma) {
    // 实部为1, 虚部为0
    Mat temp(size, size, CV_64FC2, Scalar(1.0, 0.0));
    Mat glpf = generateGLPF(size, sigma);
    Mat result = temp - glpf;
    return result;
}


Mat mulSpec(Mat spectrum1, Mat spectrum2) {
    Mat result;
    //充分保证, 输入的俩个矩阵数据类型相同.
    spectrum1.convertTo(spectrum1, CV_64F);
    spectrum2.convertTo(spectrum2, CV_64F);
    mulSpectrums(spectrum1, spectrum2, result, 0);
    return result;
}

void displayComplexImg(Mat input, string windowName, int normalMax = 255) {
    Mat planes[2];
    split(input, planes);
    Mat magnitudeRes;
    magnitude(planes[0], planes[1], magnitudeRes);
    normalize(magnitudeRes, magnitudeRes, 0, normalMax, NORM_MINMAX);
    magnitudeRes.convertTo(magnitudeRes, CV_8U);
    imshow(windowName, magnitudeRes);
}

void displayImg(Mat input, string windowName) {
    Mat result;
    normalize(input, result, 0, 255, NORM_MINMAX);
    result.convertTo(result, CV_8U);
    imshow(windowName, result);
}

测试主函数如下, 修改sigma的值为30, 60和160.

void test04(string path) {
    Mat img = imread(path, IMREAD_GRAYSCALE);
    if (img.empty()) {
        cerr << "Error: unable to load the image\n";
        return;
    }
    resize(img, img, Size(256, 256));
    Mat paddedRes = getPaddedImg(img);
    Mat dftRes = getSpectrum(paddedRes);
    Mat ghpf = generateGHPF(2 * img.r    ows, 60);
    Mat filteredSpec = mulSpec(dftRes, ghpf);
    Mat idftRes = idftImg(filteredSpec);

    displayImg(img, "原图");
    displayComplexImg(ghpf, "高通滤波器频谱");
    displayComplexImg(dftRes, "原图频谱");
    displayComplexImg(filteredSpec, "频谱相乘的结果");
    displayImg(idftRes(Rect(0, 0, img.rows, img.rows)), "逆变换的结果");
    waitKey(0);
}

6.2 拉普拉斯算子

拉普拉斯算子定义为:

$${\nabla }^{2}f=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}$$

由于其是一种微分算子, 强调的是图像中灰度的突变. 将原图像和拉普拉斯图像叠加在一起可以复原背景特性并保持拉普拉斯锐化的效果. 即

$$g(x,y)=f(x,y)+c\left[{\nabla }^{2}f(x,y)\right]$$

又${\nabla }^{2}f(x,y)={\mathcal{L}}^{-1}\left\{H(u,\nu )F(u,\nu )\right\}$, $H(u.v)=-4{\pi }^2{D}^2(u,v)$

所以锐化的结果为:

$$g(x,y)={\mathcal{L}}^{-1}\left\{[1+4{\pi }^2{D}^2(u,\nu )]F(u,\nu )\right\}$$

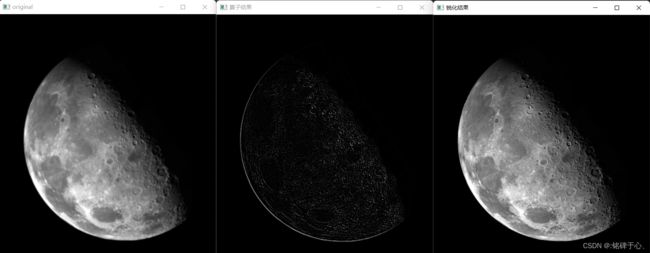
具体的opencv实现如下:（可以发现月球上的坑边明显了）

Mat generateLaplacianFilter(int rows, int cols) {
    Point center(rows / 2, cols / 2);
    Mat filter(rows, cols, CV_64FC2);
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            double distance = norm(Point(i, j) - center);    //求绝对范数(两点距离)
            filter.at<Vec2d>(i, j) = Vec2d(-4 * CV_PI * CV_PI * distance * distance, 0.0);
        }
    }
    return filter;
}

// 测试拉普拉斯滤波器
void test05(string path) {
    Mat img = imread(path, IMREAD_GRAYSCALE);
    if (img.empty()) {
        cerr << "Error: Unable to load the image.\n";
        return;
    }
    Mat paddedRes = getPaddedImg(img);
    Mat dftRes = getSpectrum(paddedRes);
    Mat lapFilter = generateLaplacianFilter(2 * img.rows, 2 * img.cols);
    Mat mulSpecRes = mulSpec(dftRes, lapFilter);
    Mat idftRes = idftImg(mulSpecRes);

    Mat result = idftRes(Rect(0, 0, img.cols, img.rows));
    result.convertTo(result, CV_8U);    //为了相减, 相减之前改变数据类型
    displayImg(img, "original");
    //displayComplexImg(lapFilter, "拉普拉斯滤波器");
    //displayComplexImg(dftRes, "原图频谱图");
    displayImg(result, "算子结果");
    displayImg(img - result, "锐化结果");    //c取-1
    waitKey(0);
}

6.3 同态滤波

核心思想是, 一幅图像表示为照射分量和反射分量的乘积. 照射分量通常由慢的空间变化来表征, 而反射分量往往引起突变, 特别在不同物体的连接部分.

因此适用于光照条件较大(非均匀照明)的图像中.

代码实现如下：

//测试同态滤波
Mat getHomomorFiilter(Mat input, double rh, double rl, double sigma, int c) {
	int rows = input.rows;
	int cols = input.cols;
	Mat filter(rows, cols, CV_64FC2);
	for (int i = 0; i < rows; i++) {
		for (int j = 0; j < cols; j++) {
			double d2 = pow(i - rows / 2, 2) + pow(j - cols / 2, 2);
			double value = (rh - rl) * (1 - exp(-1 * c * d2 / (sigma * sigma))) + rl;
			filter.at<Vec2d>(i, j) = Vec2d(value, 0);
		}
	}
	return filter;
}

void test06(string path) {
	Mat img = imread(path, IMREAD_GRAYSCALE);
	if (img.empty()) {
		cerr << "Error: Unable to load the image.\n";
		return;
	}
	resize(img, img, Size(373, 581));
	img.convertTo(img, CV_32F, 1.0 / 255); //这里归一化很重要，因为后续操作有e，有ln，利于最后的图像显示
	//第一步取ln
	Mat logImg;
	log(1.0 + img, logImg);

	Mat paddedRes = getPaddedImg(logImg);
	Mat dftRes = getSpectrum(paddedRes);
	Mat filter = getHomomorFiilter(paddedRes, 2.0, 0.25, 80, 1);
	Mat mulSpecRes = mulSpec(dftRes, filter);
	Mat idftRes = idftImg(mulSpecRes);
	//最后一步，反指数变换
	exp(idftRes, idftRes);
	idftRes -= 1.0;
	Mat result = idftRes(Rect(0, 0, img.cols, img.rows));

	displayImg(img, "原图");
	displayImg(result, "结果");
	waitKey(0);
}

6.4 小结

后面的滤波器操作大同小异， 只要给出滤波器的函数，通过代码构建出来，再按照4.2中的步骤一步一步来即可。

实际操作中需要注意的是，运算过程中一定要保持俩个操作矩阵的数据类型是一样的。

opencv补充:

1. cv::dft()函数, 其flags参数有以下形式:

   • DFT_COMPLEX_OUTPUT: 输出是一个复数矩阵. 如果没有设置此标志, 则输出的是大小等于输入的幅度矩阵.
   • DFT_REAL_OUTPUT: 仅在逆变换中使用, 指定输出是实数矩阵.
   • DFT_INVERSE: 执行傅里叶逆变换.
   • DFT_ROWS: 指定在每行上独立执行傅里叶变换.
   • DFT_SCALE: 变换结果会进行缩放, 以便更好的处理幅度的变化.

2. opencv中数据类型的命名规则

   • CV_8U：8位无符号整数（unsigned char）
   • CV_8S：8位有符号整数（char）
   • CV_16U：16位无符号整数（unsigned short）
   • CV_16S：16位有符号整数（short）
   • C1：单通道
   • C2：双通道
   • C3：三通道