数据结构：树详解

创建二叉树

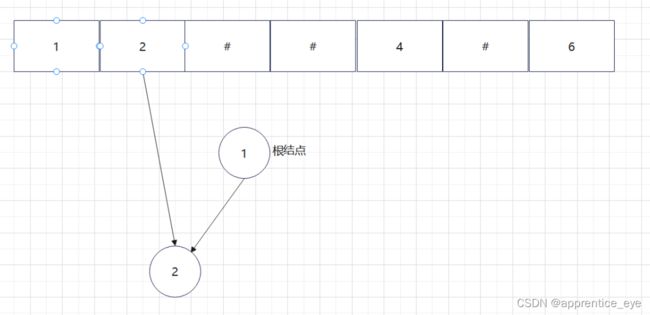
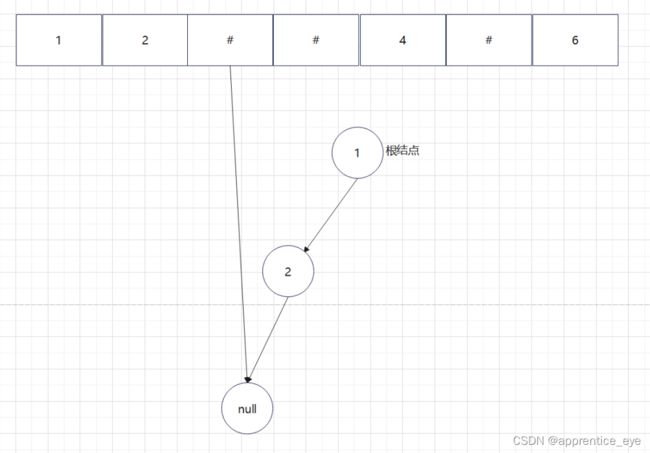
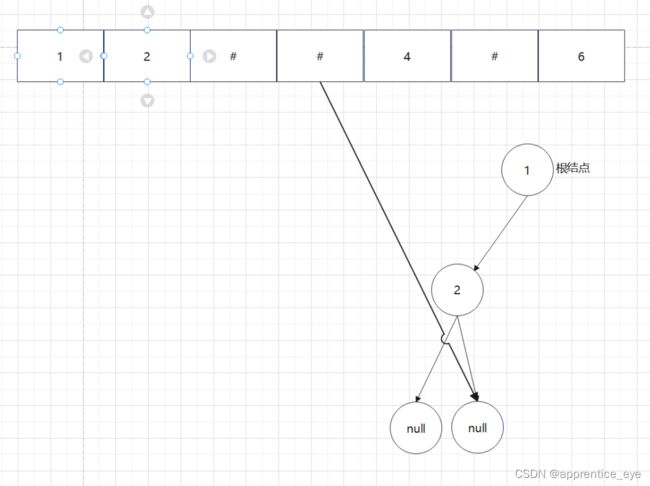
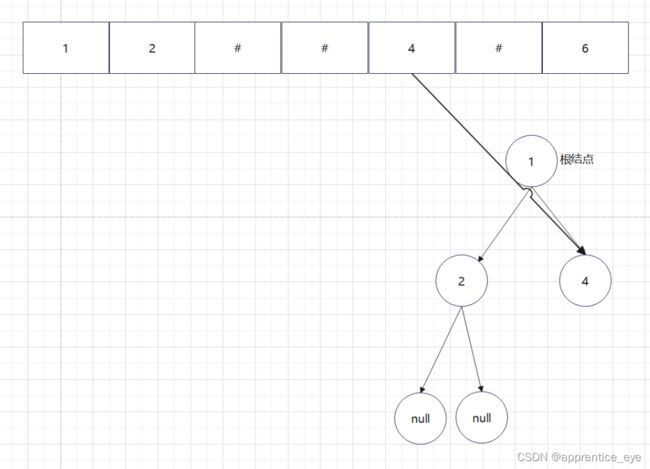
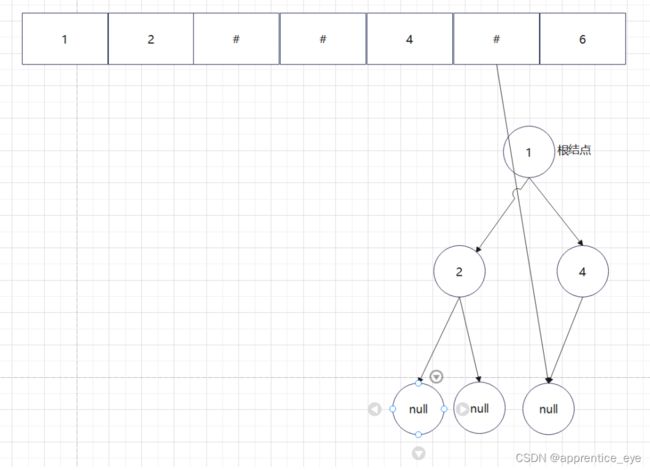
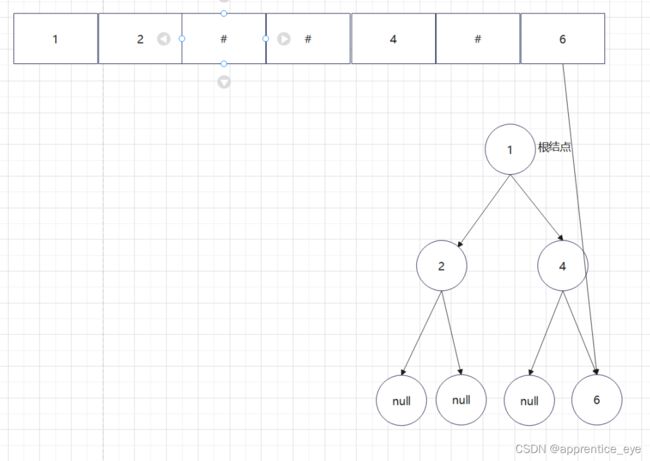
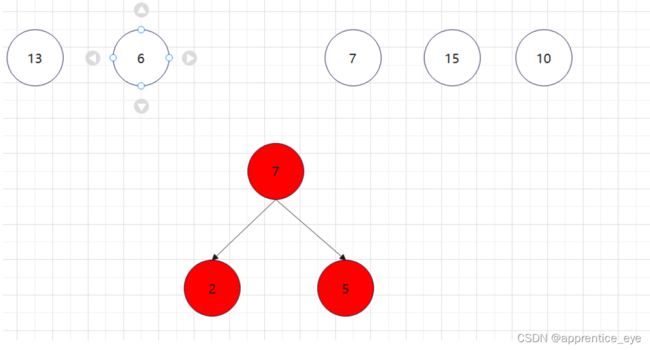
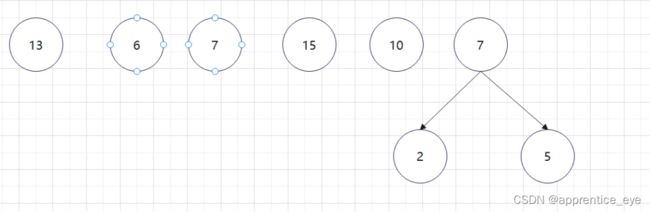
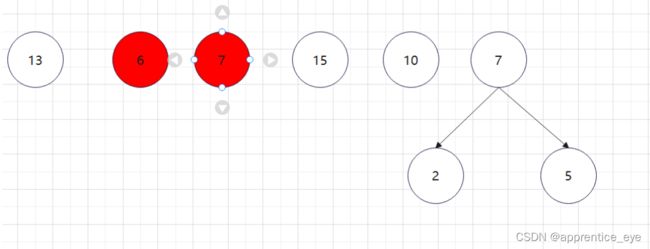
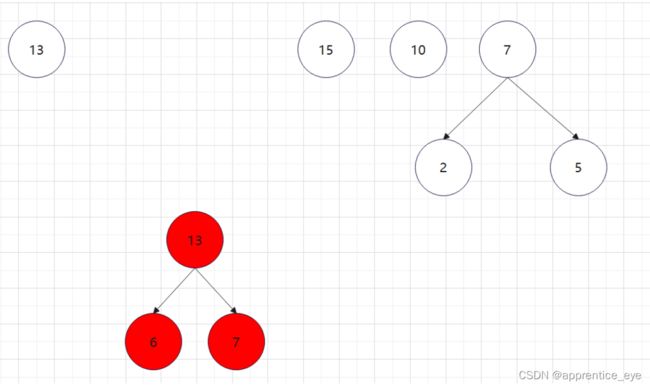
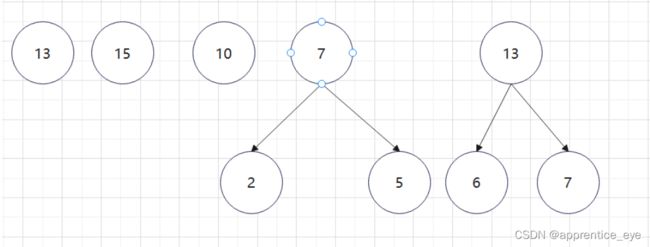
给出了完整的先序遍历序列，子树为空用’#’表示，所以这样我们在通过先序遍历序列创建二叉树时我们直到先序遍历序列是先进行根结点，然后左子树最后右子树的顺序进行遍历的，所以对于完整的先序遍历序列我们可以直到先序遍历序列中第一个元素是二叉树的根结点，如果第二个元素不为’#’，那么这个代表二叉树有左孩子，而且左孩子的值为先序遍历序列的第二个元素的值，依次类推，根据二叉树的完整先序遍历序列我们可以直到每一个结点是否为空，这样我们就能够采取递归形式进行二叉树的创建：
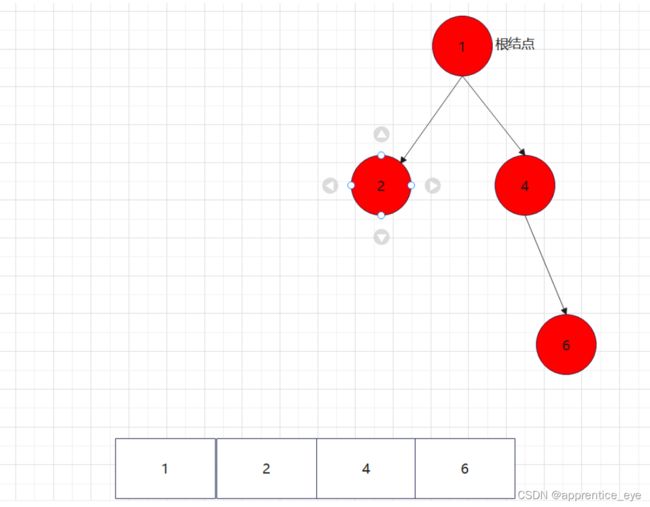
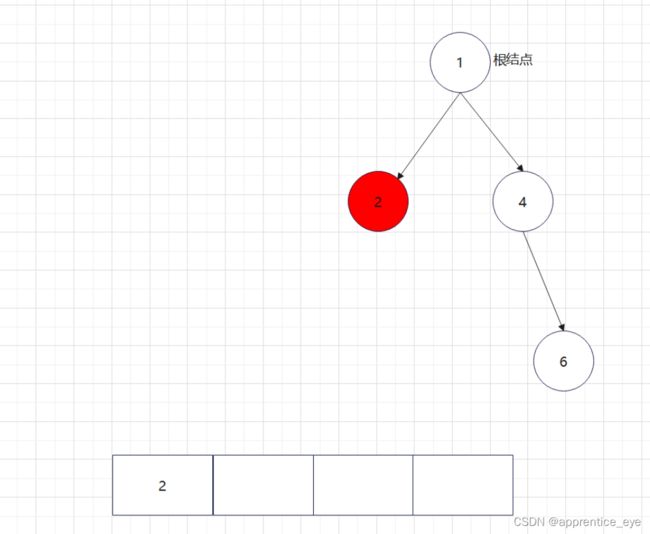
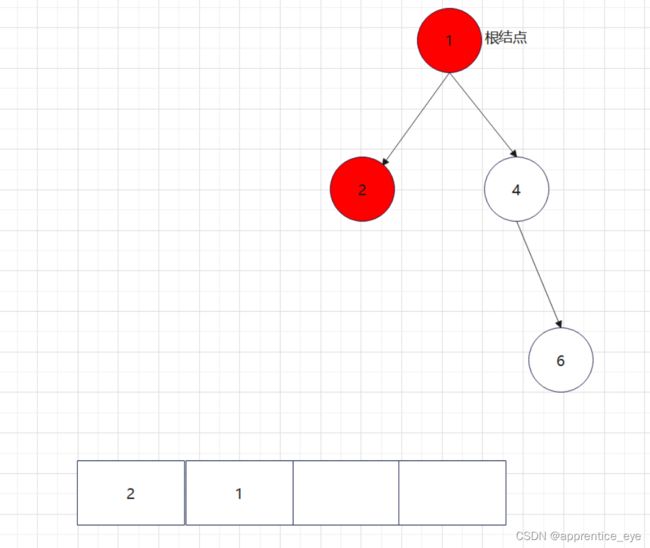
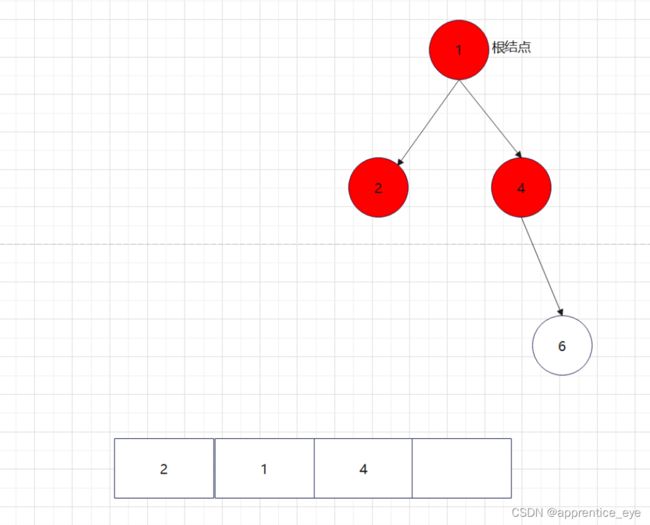
创建过程的图示为如下：

最终我们得到的树如下图所示：

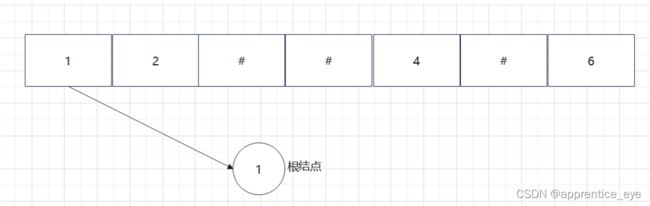
有了上面的思路我们可以写出如下代码：

void InitBinaryTree(char *p, int *length, struct BinaryTreeNode **root){
	if(p[*length]!=0){
		if(p[*length]!='#'){
			*root = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
			(*root)->val = p[*length];
			(*root)->left = NULL;
			(*root)->right = NULL;
			(*length)++;
			InitBinaryTree(p, length, &(*root)->left);
			InitBinaryTree(p, length, &(*root)->right);	
		}else{
			(*length)++;
		}
	}
}

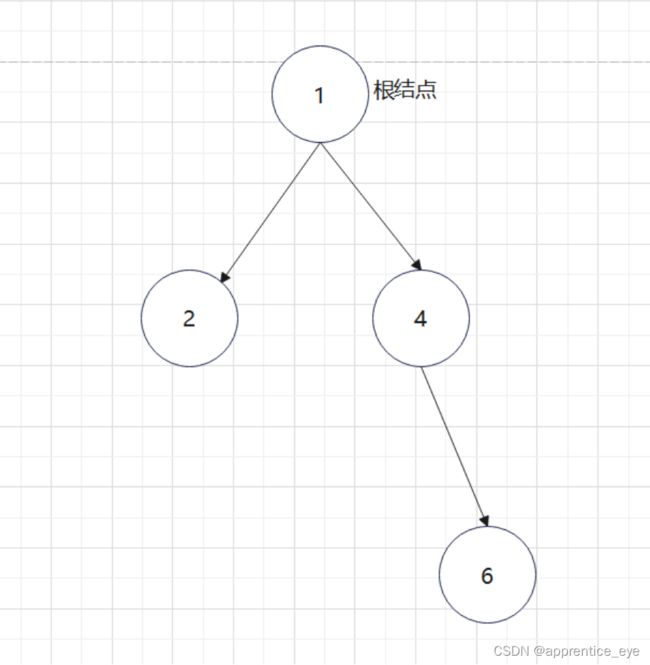
这就是通过树的完整前序遍历序列创建二叉树的过程。
下面我们来进行实现二叉树的前序遍历、中序遍历与后序遍历，前序遍历是指先根结点再左子树最后右子树，中序遍历是先左子树然后根结点最后右子树，后序遍历是先左子树然后右子树最后根结点，这种遍历可以通过递归进行实现，在每次递归中所在结点不为NULL就说明结点有值，我们需要遍历这一个结点的左子树与右子树，也就是递归截至的条件是root==NULL;有了这样的思路前序遍历与中序遍历，与后序遍历就只是根结点的访问顺序发生改变，我们可以写出下面的三种遍历的代码：
前序遍历：

//本函数实现二叉树的前序遍历功能
void preOrderTraversal(struct BinaryTreeNode *root){
	if(root!=NULL){
		printf("%c ", root->val);
		preOrderTraversal(root->left);
		preOrderTraversal(root->right);	
	}
}

中序遍历：

//本函数实现二叉树的中序遍历功能
void inOrderTraversal(struct BinaryTreeNode *root){
	if(root!=NULL){
		inOrderTraversal(root->left);
		printf("%c ", root->val);
		inOrderTraversal(root->right);	
	}
}

后序遍历：

// 本函数实现二叉树的后序遍历功能
void postOrderTraversal(struct BinaryTreeNode *root){
	if(root!=NULL){
		postOrderTraversal(root->left);
		postOrderTraversal(root->right);
		printf("%c ", root->val);	
	}
}

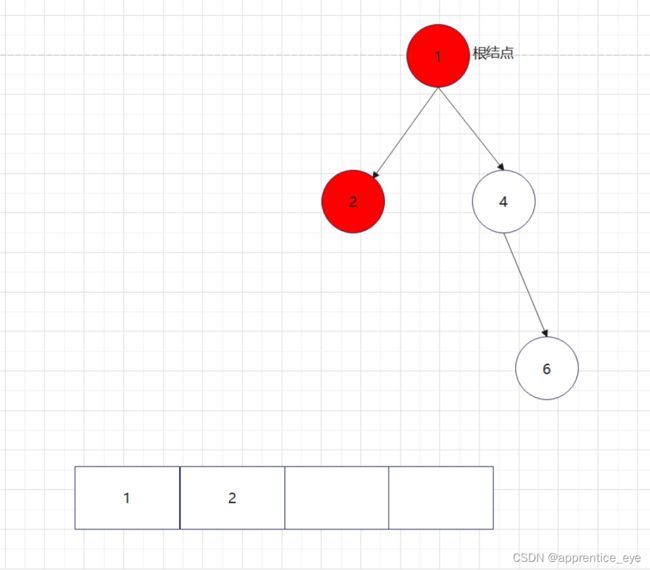
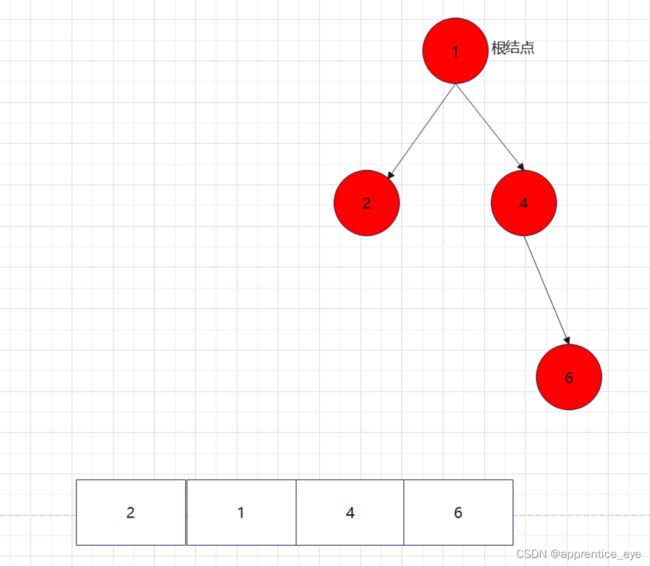
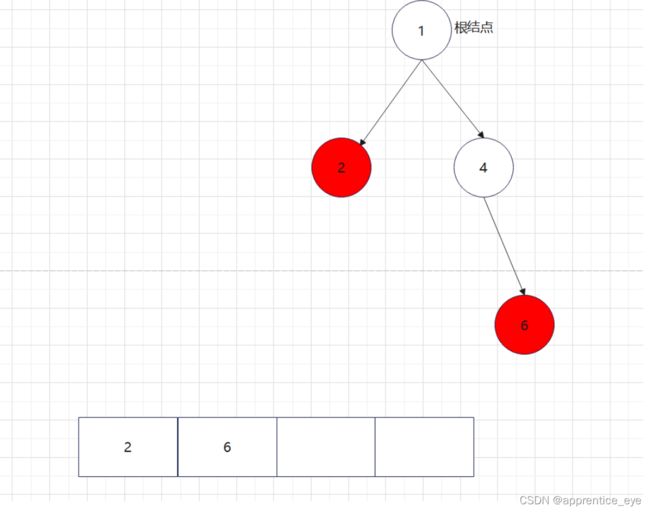
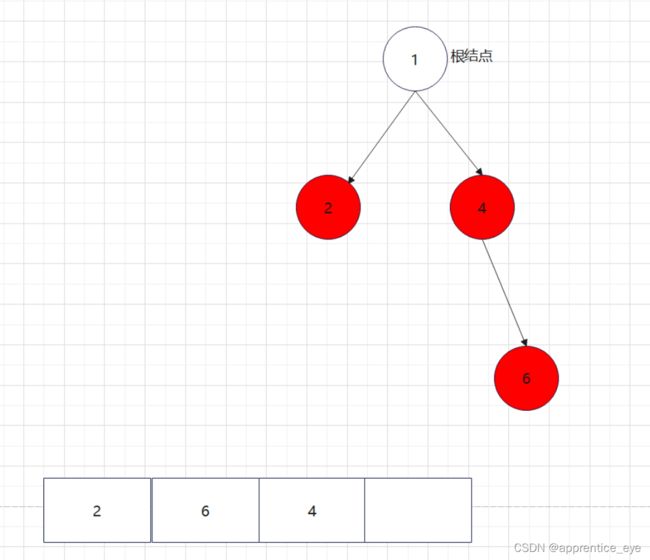
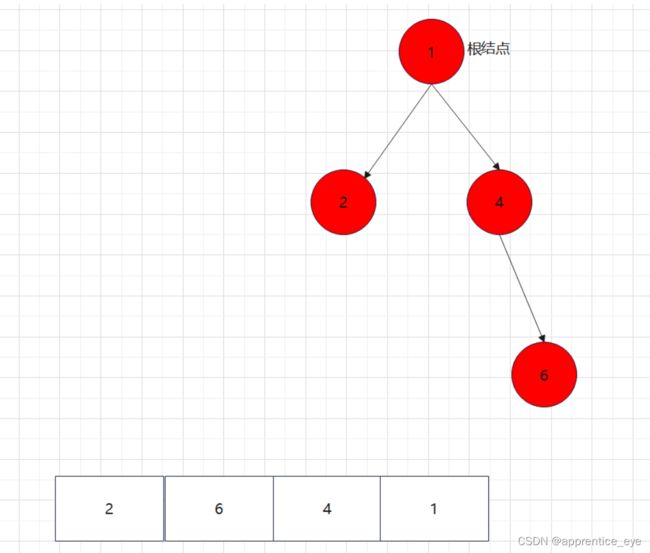
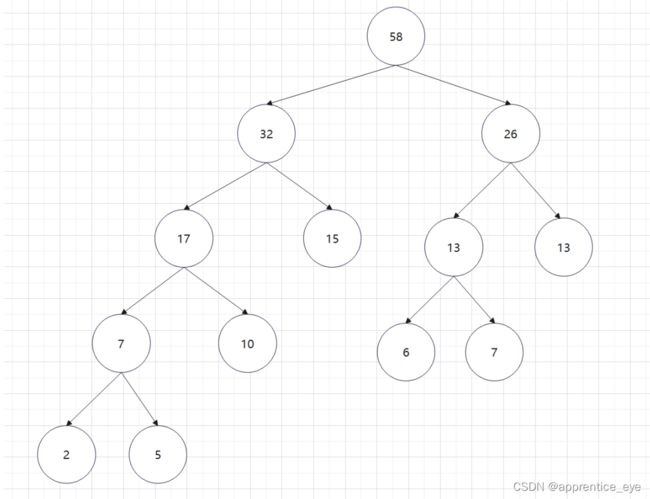
就以上面的建立的二叉树为例查看一下该二叉树的前序遍历序列、中序遍历序列、后序遍历序列。
二叉树的前序遍历序列应为：

中序遍历序列应为：

后序遍历序列应为：

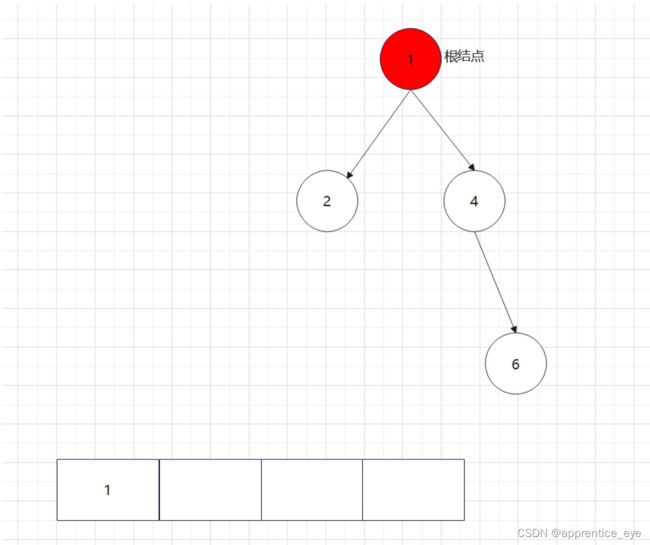
我们来运行一下看看结果是否正确：

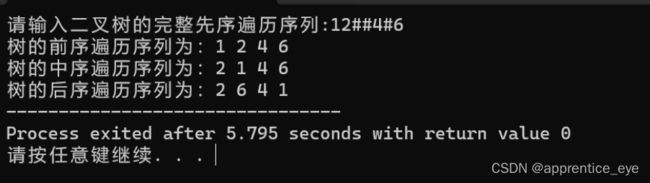
可以看出结果确实正确。
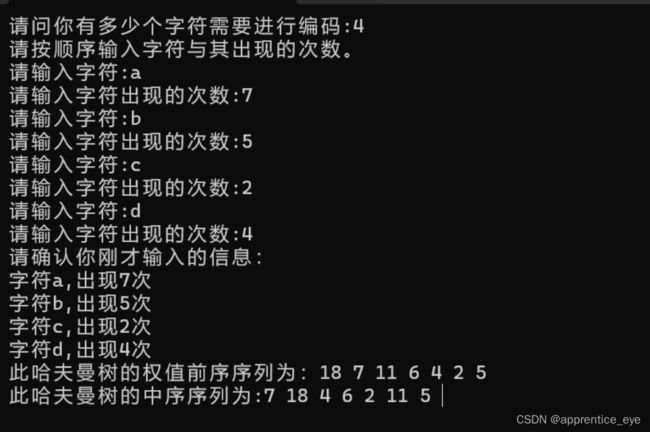
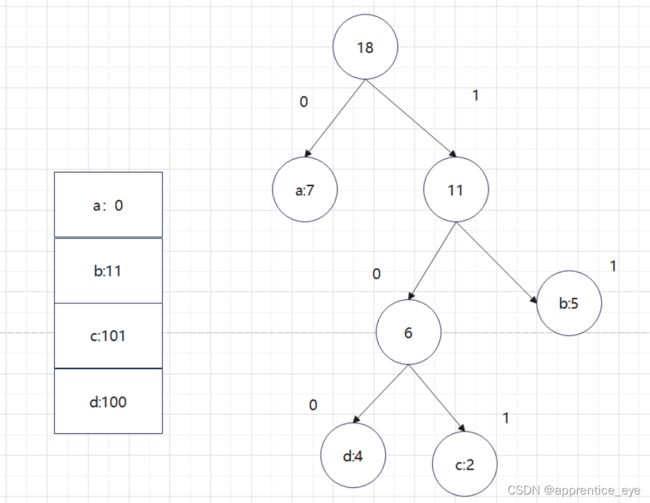
至此关于二叉树的内容已经全部实现，接下来实现哈夫曼树以及编码操作，题目中给出了’a’ ‘b’ ‘c’ ‘d’以及其对应出现的次数分别是7、5、2、4，出现次数多的字母编码要尽可能的短，我们可以利用哈夫曼树来实现对应的操作，哈夫曼树是为每个结点增加一个权值，权值大的结点离根要尽可能的近，我们就可以将所有的字符视作只有一个根结点的树，将结点权值小的两个子树进行合成组成一颗新树，两个子树的权值之和作为新树的权值，这一颗新树与剩余的所有树组成一个新的集合，然后从中选取两个树进行上述过程，如此重复下去，直到剩下一棵树，这棵树就是哈夫曼树。图示如下：

如此进行下去最后只剩下一棵树：

这就是哈夫曼树，所以只需要将字母出现的次数作为权值，按照上述规则我们就能够生成一颗哈夫曼树。代码如下：

#include
#include
struct BinaryTreeNode{
	int weight;
	char val;
	struct BinaryTreeNode * left;
	struct BinaryTreeNode * right;
};
//对子树按照权值进行降序排列，这样只操作最后面的两棵树就行了
void sort(struct BinaryTreeNode ** p, int length){
	for(int i=0;i<length-1;i++){
		for(int j=0; j<length-1; j++){
			if(p[j]->weight<p[j+1]->weight){
				struct BinaryTreeNode * t = p[j];
				p[j] = p[j+1];
				p[j+1] = t;
			}
		}
	}
}
//创建哈夫曼树
struct BinaryTreeNode * InitHuffmanTree(struct BinaryTreeNode ** p, int length){
	struct BinaryTreeNode * root = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
	while(length!=2){
		sort(p, length);
		root->left = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
        *(root->left) = *p[length-2];
		root->right = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
        *(root->right) = *p[length-1];
        root->val = 0;
		root->weight = p[length-2]->weight+p[length-1]->weight;
        free(p[length-1]);
        free(p[length-2]);
		p[length-2] = root;
		root = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
		length -= 1;
	}
	root->left = p[length-2];
	root->right = p[length-1];
	root->weight = p[length-2]->weight+p[length-1]->weight;
	return root;
}
//前序遍历
void preOrderTraversal(struct BinaryTreeNode *root){
	if(root!=NULL){
		printf("%d ", root->weight);
		preOrderTraversal(root->left);
		preOrderTraversal(root->right);	
	}
}
//中序遍历
void inOrderTraversal(struct BinaryTreeNode *root){
	if(root!=NULL){
		inOrderTraversal(root->left);
		printf("%d ", root->weight);
		inOrderTraversal(root->right);	
	}
}
int main(){
	int n;
	char code[4][20];
	printf("请问你有多少个字符需要进行编码:");
	scanf("%d", &n);
	struct BinaryTreeNode ** p = (struct BinaryTreeNode **)malloc(sizeof(int)*n);
	printf("请按顺序输入字符与其出现的次数。\n");
	for(int i=0; i<n; i++){
		p[i] = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
		p[i]->left = NULL;
		p[i]->right = NULL;
		printf("请输入字符:");
		getchar();
		scanf("%c", &p[i]->val);
		getchar();
		printf("请输入字符出现的次数:");
		scanf("%d", &p[i]->weight);
	}
	printf("请确认你刚才输入的信息：\n");
	for(int i=0; i<n; i++){
		printf("字符%c,出现%d次\n", p[i]->val, p[i]->weight);
	}
	struct BinaryTreeNode * root = InitHuffmanTree(p, n);
	printf("此哈夫曼树的权值前序序列为：");
	preOrderTraversal(root);
	printf("\n此哈夫曼树的中序序列为:");
	inOrderTraversal(root);
	return 0;
}

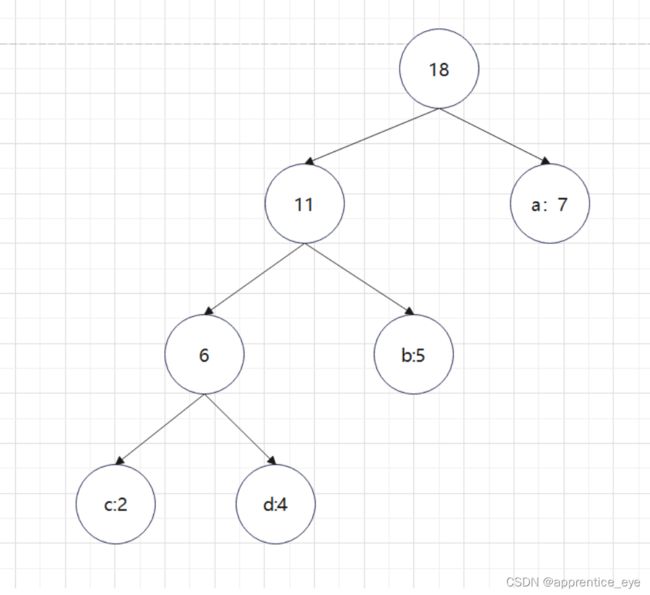
根据权值的前序序列与中序序列可以建立如下二叉树：

因为出现在叶子结点的才是字符，所以我们可以直到权值为7的结点时’a’，权值为4的结点是’d’，权值为2的结点是’c’,权值为5的结点时’b’，即如下图所示：

按照哈夫曼树的建立规则进行手动建树，可以建出以下这个树:

可以看出这两棵树是等价的，只不过是左右孩子交换了下顺序，也就是说明了程序是正确的。接下来就是进行哈夫曼编码了。
向左为0，向右为1进行编码，进行二进制编码，可以写出下面的代码：

void HuffmanCode(struct BinaryTreeNode *root, char n[20], char p[][20], int length){
	//p用来存储编好的编码
	if(root!=NULL){
		switch(root->val){
			case 'a':	
			case 'b':
			case 'c':
			case 'd':
				int i;
				for(i=0;i<length;i++){
					p[root->val-'a'][i]=n[i];
				}
				p[root->val-'a'][i]='\0';
		}
		n[length++] = '0';
		n[length] = 0;
		HuffmanCode(root->left, n, p, length);
		length--;
		n[length++] = '1';
		n[length] = 0;
		HuffmanCode(root->right, n, p,length);
	}
}

对上面的树进行编码

运行结果：

可以看到确实生成了哈夫曼编码。

如果有什么地方讲的不好或者讲错的地方欢迎大家指出来，如果我所讲的对你们有帮助不要忘了点赞、收藏、关注哦！

我是你们的好伙伴apprentice_eye

一个致力于让知识变的易懂的博主。