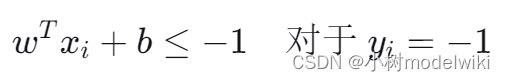支持向量机SVM模型里的二元线性分类是什么

本篇转载自 二元线性分类 - 数模百科

如果对支持向量机SVM模型的所有知识点感兴趣，请移步 支持向量机 - 数模百科

二元线性分类是指我们有两个类别的分类任务，而且这两个类别是可以被一个直线（在高维空间称为超平面）完全分开的。在二维空间中，这条直线叫做决策边界，所有在一侧的点被分类为一类，而在另一侧的点被分为另一类。在三维空间中，我们可以尝试用一个二维平面去区分两个类别。以此类推，当我们在一个n维空间中时，我们可以用一个n-1维的工具去区分不同类别。

举个例子，我们有一些点，这些点分布在纸上，有的点代表着苹果，有的点代表着橘子。我们的任务是找到一种方法，可以通过画一条线来区分这些苹果和橘子。这条线的一侧全是苹果，而另一侧全是橘子。这就是二元线性分类，我们通过一条直线来区分两类不同的物品。如果我们的苹果和橘子不是在纸上，而是在房间里的不同位置，那么我们就需要用一面墙（想象中的）来区分它们。在房间中，这面墙就像是我们在纸上画的那条线，将苹果和橘子分开。

SVM使用超平面进行二元线性分类，通过最大化间隔来找到一个能够将样本正确分类的超平面，并通过合页损失函数进行优化。

超平面的概念

超平面是数学和机器学习领域中一个非常基础且重要的概念。为了便于理解，我们可以从二维和三维空间中的例子出发，逐步深入到更高维度的概念理解中去。

首先，我们来看二维空间，也就是我们平时所说的平面。在这个平面中，我们可以画很多条直线，每一条直线都可以把平面分割成两个部分。这样的直线，实际上就是二维空间中的“超平面”。直线是一维的，比二维空间少一维。

再来看三维空间，也就是我们生活的空间。在这里，我们可以画出许多个平面，每个平面都将空间分割成两部分。在三维空间中，这些平面就是“超平面”。平面是二维的，比三维空间少一维。

更一般地，在一个n维的欧几里得空间中，超平面是n-1维的。它能够将空间分割成两个部分。可以把超平面想象成一个无限大的“板”，它通过空间中某些特定的点，并且所有在这个“板”上的点都满足一个特殊的方程。

这个方程可以用数学语言写成如下形式：

在这个方程中：

• w 是一个n维的向量，称为超平面的法向量，它垂直于超平面。

• x 是超平面上任意一点的位置向量。

• b 是一个常数，称为偏移量或截距，它决定了超平面在空间中的具体位置。

如果我们将数据点画在n维空间中，超平面就可以用来将这些点分开。在机器学习中，尤其是在支持向量机（SVM）模型中，超平面的概念非常关键。在SVM模型中，我们希望找到一个超平面，它不仅能正确地将数据分类，而且能使得不同类别的数据之间的间隔（距离）最大化。这个间隔最大的超平面就被称为最大间隔超平面。

我们希望找到的这个最大间隔超平面，其实就是找到一组最佳的 w 和 b ，使得超平面能够最好地完成分类任务，同时保持最大的分类间隔。这样的超平面能够提供更好的泛化能力，即对未知数据的分类表现更加稳健。

最大化间隔

在二元分类问题中，我们试图找到一个决策边界或一个“线”，有效地将两类分开。

这里的关键前提是，这条线是基于我们现有的数据，也就是训练数据来创建的。然而，在现实生活中，我们在未来遇到的数据（测试数据）可能并不完全与我们的训练数据相同。几乎总是存在一些变化，这些变化被称为“噪声”。

那么，为什么最大化间隔很重要呢？

想象一下，我们的决策边界是一条非常薄的线，仅仅勉强将训练数据中的两类分开。现在，当我们遇到一些包含轻微变化（噪声）的新数据时，这条薄线可能无法有效地将这两类保持分开。噪声可能会导致一些类别A的实例跨越到类别B的一侧，反之亦然，从而导致高误差率。

现在，让我们考虑一种情况，我们在两类之间有一个厚厚的边界或大的间隔。即使新数据中含有一些噪声，这个大的间隔也可以吸收这些变化，使类别A保持在一边，类别B保持在另一边。这将导致分类的误差率降低。

因此，最大化间隔或确保类别之间有良好的距离，可以增加我们模型的鲁棒性和处理数据变化的能力，最终提高其在未知数据上的性能。

这就是最大化间隔的概念。具体来说，间隔指的是数据点到分界线或超平面的最短距离。在支持向量机中，我们的目标是找到能够最大化这个间隔的超平面。

为了数学化地描述这个问题，我们可以使用一些线性代数的知识。首先，定义超平面的方程为：

在这里，w 是一个权重向量，b 是一个偏置项，x 是我们的数据点。要使得这个超平面有最大的间隔，我们希望正类（）和负类（）的数据点至少满足以下条件：

以上两个不等式确保了所有的数据点到超平面的距离至少为1。间隔就是两个类别到超平面的最近点之间的距离，计算公式为：

在这里，||w|| 表示向量 w 的范数，它反映了超平面的“斜率”。要最大化间隔，就是要最小化 ||w||，或者更具体地，最小化 （这样做是为了方便后面的数学运算，因为平方函数有良好的导数性质）。

所以，最大化间隔的优化问题可以表示为：

即在满足所有数据点正确分类的条件下，我们要找到最小化  的 w 和 b。

解决这个优化问题的一种方法是使用拉格朗日乘子法，这是一种处理带约束优化问题的强有力的数学工具。通过这种方法，我们可以找到最大化间隔的超平面，从而构建一个强健的分类器。

Hinge函数（合页损失函数）

当我们说“最大化间隔”时，我们的目标是选择一个决策边界，使得最近的正样本和负样本到这个边界的距离尽可能大。这个距离称为“间隔”。

合页损失函数（Hinge Loss Function）是用于支持向量机中的一种损失函数，它是一种用于“最大化间隔”目标的损失函数。也就是说，因为我们的目标是希望找到那些可以将正样本和负样本正确且完全分开的决策边界，所以我们需要一个损失函数来衡量一个特定的决策边界会对这个目标造成多大的破坏。

合页损失函数的定义如下：

其中，

• y 表示样本的真实标签，对于二分类问题，y 的值通常是 +1 或 -1。

• x 是样本的特征向量，可以理解为该样本各个特征的数值。

• w 是我们试图找到的分类超平面的权重，可以理解为超平面的方向。

• b 是截距项，它决定了超平面沿着特征空间的位置。

在合页损失函数中，表达式 被称为函数间隔。当一个样本被正确分类，并且函数间隔大于1时，我们可以认为这个样本距离决策边界有足够的安全距离，因此它的损失是0。这意味着这个样本对我们的决策边界的选择没有负面影响。

然而，如果样本被错误分类，或者即使它被正确分类，但函数间隔小于1（即它离决策边界太近），那么损失就是 。这种情况下的损失值代表了样本距离我们希望的决策边界有多远，或者说我们的决策边界离最优解还需改进的程度。

合页损失函数的一个优点是它是凸的，这意味着我们可以使用凸优化技术来找到全局最优解。当我们在训练过程中最小化合页损失时，我们实际上是在尝试找到一个可以最大化类别间隔，并且对错误分类的样本施加一定惩罚的决策边界。

总结来说，合页损失函数帮助支持向量机处理分类问题，即使数据在特征空间中不是完全线性可分的。通过软间隔的概念，它允许一些样本违反间隔规则，但会给这些样本施加损失，以保证整体模型的性能。

本篇文章摘录自 数模百科 ——  二元线性分类 - 数模百科

数模百科是一个由一群数模爱好者搭建的数学建模知识平台。我们想让大家只通过一个网站，就能解决自己在数学建模上的难题，把搜索和筛选的时间节省下来，投入到真正的学习当中。

我们团队目前正在努力为大家创建最好的信息集合，从用最简单易懂的话语和生动形象的例子帮助大家理解模型，到用科学严谨的语言讲解模型原理，再到提供参考代码。我们努力为数学建模的学习者和参赛者提供一站式学习平台，目前网站已上线，期待大家的反馈。

如果你想和我们的团队成员进行更深入的学习和交流，你可以通过公众号数模百科找到我们，我们会在这里发布更多资讯，也欢迎你来找我们唠嗑。