双重差分法之安慰剂检验
简单介绍一下实证论文中双重差分法(DID)的安慰剂检验(Placebo Test)在Stata中如何操作。
(本文首发于个人微信公众号DMETP,是往期两篇推文的合辑,欢迎关注!)
下面的内容根据实际使用的数据集分为两个部分。
-
一是以一个截面数据集为例,介绍一下安慰剂检验的整个思路与流程。这里使用的是系统数据集
auto.dta,由于是简单介绍思路,因此该部分并没有第二部分面板数据那么复杂,且模型中不包括DID的交互项,仅仅是对一个核心变量rep78进行1,000次随机抽样; -
二是以一个面板数据集为例,介绍一下面板数据DID中安慰剂检验的整个流程。这里使用的数据集是石大千等(2018)公布在《中国工业经济》网站上的附件内容。论文使用的模型是普通DID模型,也即政策发生时点(2012年)固定,处理组与控制组的设置也固定。
参考文献:
石大千, 丁海, 卫平, 刘建江. 智慧城市建设能否降低环境污染[J]. 中国工业经济, 2018(06): 117-135.
一、安慰剂检验方法选择
通常而言,DID中的安慰剂检验方法包括两种。
-
一是改变政策发生时点,具体又包括前置处理组的政策发生时点,此时安慰剂检验的作用与平行趋势检验相同,都是考察政策发生前基础回归中时间虚拟变量与处理组交互项系数(
F(-1)、F(-2)、F(-3)、…)的显著性,如果不显著说明检验通过;还包括将政策发生时点随机化,也即将时点前置或后置,这是一种更一般化的做法; -
二是将处理组随机化,对处理组变量进行一定次数的随机抽样,然后再观测随机化后的DID项系数或观测值的核密度图是否集中分布于0附近,以及是否显著偏离其真实值;
-
第二种方法更为常见,第一种方法的不足在于:如果样本期间较短,导致随机抽样的时段区间过短,得出的结论不一定真实,虽然抽样次数可以很多,但抽样空间过短将影响结论的稳健性。综合来说,对处理组进行随机化处理是一种更为合适的做法。当然,具体论文要具体分析。
二、截面数据集的安慰剂检验
这部分代码使用的是Stata系统自带的数据集auto.dta,该数据集是截面数据且不包含DID项,在实际使用中,可以将reg改为面板数据回归命令(如xtreg、reghdfe等),同时将这里的核心解释变量rep78改为论文中需要进行随机化处理的关键变量。
需要提醒的是,陆菁等(2021)在随机化处理时,提到“DID模型估计要求政策实施年份前后至少有一年数据”,因此在时间窗口不长且需要进行安慰剂检验的情况下,需要特别注意这一点。
参考文献:
陆菁, 鄢云, 王韬璇. 绿色信贷政策的微观效应研究——基于技术创新与资源再配置的视角[J]. 中国工业经济, 2021(01): 174-192.
此外,代码部分还参考了李青原和章尹赛楠(2021)发表在中国工业经济上的一篇文章的附件,同时还参考了简书的一篇文章。
参考文献:
李青原, 章尹赛楠. 金融开放与资源配置效率——来自外资银行进入中国的证据[J]. 中国工业经济, 2021(05): 95-113.
2.1 整体思路
-
第一步:在原始数据集
auto.dta中单独剔除核心变量rep78的样本数据; -
第二步:将剔除出来的
rep78随机打乱顺序,再将随机化的rep78合并至已被处理过的原始数据集中; -
第三步:将随机化的
rep78放入回归方程中进行回归; -
第四步:以上操作步骤重复1,000次;
-
第五步:单独提取出1,000次回归结果中
rep78的系数与标准误,最后分别绘制系数和t值的核密度分布图以及P值 - 系数散点图。
2.2 代码实现
*==============================================================================*
* 双重差分法 | 安慰剂检验 *
*==============================================================================*
** Stata Version: 16 | 17
** 【文章首发】这篇文章首发于本人微信公众号『DMETP』,是两篇推文的合辑,欢迎关注!
cd "C:\Users\KEMOSABE\Desktop\placebo_test"
**# 一、截面数据的安慰剂检验
**# 1.1 根据原始样本进行基础回归
sysuse auto.dta, clear
global ctrlvar1 "mpg headroom trunk weight length"
reg price rep78 $ctrlvar , r
*- 基础回归中核心变量rep78的真实系数与真实t值分别为:
*- 真实系数 = 889.6715
*- 真实t值 = 3.2206(可手动计算,也即889.6715 / 276.2438)
clear all
**# 1.2 对rep78进行1,000次随机抽样、回归并绘制核密度图
*- 思路:
*- a. 在原始数据集auto.dta中单独剔除核心变量rep78的样本数据
*- b. 将剔除出来的rep78随机打乱顺序,再将随机化的rep78合并至已被处理过的原始数据集中
*- c. 将随机化的rep78放入回归方程中进行回归
*- d. 以上操作步骤重复1,000次
*- e. 单独提取出1,000次回归结果中rep78的系数与标准误,最后分别绘制系数和t值的核密度估计图以及P值与系数的散点图
set seed 13579 // 设置随机种子数
forvalue i = 1/1000 {
sysuse auto.dta, clear
preserve
gen randomvar = runiform()
sort randomvar
gen id = _n
label var id "用于匹配的样本序号"
keep rep78 id
save rep78_random.dta, replace // 该数据集中仅保留rep78和随机化的id
// id用于将该数据集中的rep78横向合并(merge)至原数据集
restore
gen id = _n
label var id "用于匹配的样本序号"
drop rep78
save rep78_dropped.dta, replace // 原数据集中已剔除rep78字段
use rep78_dropped.dta, clear
merge 1:1 id using rep78_random.dta, keepusing(rep78) // 将随机化排序的rep78合并至原数据集
qui reg price rep78 $ctrlvar1 , r
gen b_rep78 = _b[rep78] // 提取回归后rep78的系数
gen se_rep78 = _se[rep78] // 提取回归后rep78的标准误
keep b_rep78 se_rep78
duplicates drop b_rep78, force
save placebo_`i'.dta, replace
}
erase rep78_random.dta
erase rep78_dropped.dta
use placebo_1.dta, clear
forvalue k = 2/1000 {
append using placebo_`k'.dta // 将1,000次回归中rep78的系数和标准误纵向合并(append)至单独的数据集(placebo_1.dta)
erase placebo_`k'.dta
}
graph set window fontface "Times New Roman"
graph set window fontfacesans "宋体" // 设置图形输出的字体
gen tvalue = b_rep78 / se_rep78
gen pvalue = 2 * ttail(e(df_r), abs(tvalue)) // 计算t值和P值
**# 1.2.1 系数
sum b_rep78, detail
twoway(kdensity b_rep78, ///
xline(`r(mean)', lpattern(dash) lcolor(black)) ///
xline(889.6715 , lpattern(solid) lcolor(black)) ///
scheme(qleanmono) ///
xtitle("{stSans:系数}" , size(medlarge)) ///
ytitle("{stSans:核}""{stSans:密}""{stSans:度}", size(medlarge) orientation(h)) ///
saving(placebo_test_Coefficient1, replace)), ///
xlabel(, labsize(medlarge)) ///
ylabel(, labsize(medlarge) format(%05.4f)) // 绘制1,000次回归rep78的系数的核密度图
graph export "placebo_test_Coefficient1.png", replace // 导出为矢量图,方便论文中的图形展示;medlarge可以改为large以将标题文字加大
**# 1.2.2 P值
sum b_rep78, detail
twoway(scatter pvalue b_rep78, ///
msy(oh) mcolor(black) ///
xline(`r(mean)', lpattern(dash) lcolor(black)) ///
xline(889.6715 , lpattern(solid) lcolor(black)) ///
yline(0.1 , lpattern(shortdash) lcolor(black)) ///
scheme(qleanmono) ///
xtitle("{stSans:系数}" , size(medlarge)) ///
ytitle("{stSans:P}""{stSans:值}" , size(medlarge) orientation(h)) ///
saving(placebo_test_Pvalue1, replace)), ///
xlabel( , labsize(medlarge)) ///
ylabel(0(0.25)1, labsize(medlarge) format(%03.2f))
graph export "placebo_test_Pvalue1.png", replace
**# 1.2.3 t值
sum tvalue, detail
twoway(kdensity tvalue, ///
xline(`r(mean)', lpattern(dash) lcolor(black)) ///
xline(3.2206 , lpattern(solid) lcolor(black)) ///
xline(-1.65 , lpattern(shortdash) lcolor(black)) ///
xline( 1.65 , lpattern(shortdash) lcolor(black)) ///
scheme(qleanmono) ///
xtitle("{stSans:t值}" , size(medlarge)) ///
ytitle("{stSans:核}""{stSans:密}""{stSans:度}", size(medlarge) orientation(h)) ///
saving(placebo_test_Tvalue1, replace)), ///
xlabel(, labsize(medlarge)) ///
ylabel(, labsize(medlarge) format(%02.1f)) // 绘制1,000次回归rep78的t值的核密度图
graph export "placebo_test_Tvalue1.png", replace
erase placebo_1.dta
discard
clear all
cls
2.3 运行结果与解读
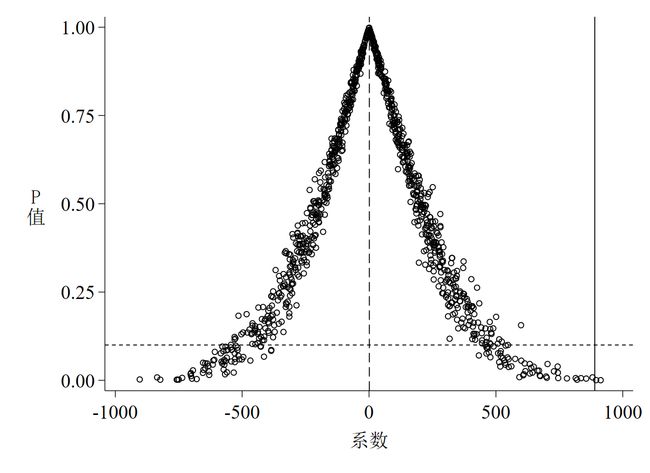
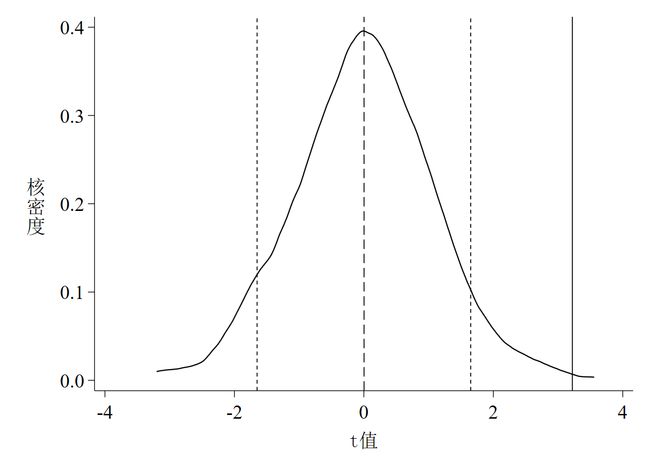
以上这段代码的运行结果是3张图,如下所示。其中图 1是系数的核密度估计图;图 2是P值 - 系数散点图;图 3是t值的核密度估计图。
针对图 1至图 3的解读如下:
-
随机化核心解释变量后系数与t值的核密度估计值的均值都接近于0(分别为1.2233和0.0029);
-
随机化后系数与t值的核密度估计值的均值都大大偏离其真实值(真实值分别为889.6715和3.2206);
-
随机化后多数系数的P值位于
P value = 0.1线以上,说明多数系数至少在10%的水平下不显著; -
以上三点均说明
rep78对price的影响不是由其他不可观测因素(或遗漏变量)推动的; -
设置随机种子数为13,579时,可重复以上结果并得出一致结论;
-
从P值的散点图可以得到以下两点信息:
- 第一,更多的散点集中分布于0附近,而位于真实值垂直线上的散点只有几个,这说明在随机化后真实值是一个异常点;
- 第二,虽然多数散点集中于0附近,但这些散点所代表的系数至少在10%的水平上是不显著的。
三、面板数据集的安慰剂检验
前面一部分介绍了安慰剂检验的具体操作,但都是以一个截面数据集(auto.dta)作为示例的,且模型中没有加入DID的交互项,因此严格来说这个例子还不太恰当。这里用一个具体例子介绍面板数据双重差分模型中的安慰剂检验,这个例子是一个普通DID模型,政策发生时点固定,处理组和控制组也是固定的,相对而言模型设置比较简单,但也可以延伸至相对复杂的DID模型中(如多期DID、连续DID和广义DID等),所需的可能仅仅是要发挥更多的想象力。
原始数据来源于石大千(2018),但这篇文章和中国工业经济官网放出来的附件都没有详细解释处理组和控制组的具体设置,因此虽然可以用gen dt = (year >= 2012)生成政策发生时间虚拟变量(dt),但处理组虚拟变量(du)无法生成,因此这里使用的是公众号『功夫计量经济学』提供的数据,数据有效性本人无法保证,这里只作为一个参考示例。
关于论文的具体内容详见参考文献,这里不做介绍,也可以快速浏览『功夫计量经济学』的相关推文。值得一提的是,『功夫计量经济学』给出了另外一种随机抽样的方法,可以与本推送给出的方案对照阅读。
这里设置了一个随机种子(seed),方便复现结果与推送内容保持一致,随机种子数是223,至于为什么是这个数,纯粹是试错试出来的,因为设置成这个数画出来的图最好看。
3.1 整体思路
-
第一步:在原始数据集
smart_city2018.dta中单独剔除变量id的样本数据; -
第二步:将剔除出来的
id随机打乱顺序,再将随机化的id合并至已被处理过的原始数据集中; -
第三步:将随机化的
treat与dt的交互项(did)放入回归方程中进行回归; -
第四步:以上操作步骤重复1,000次;
-
第五步:单独提取出1,000次回归结果后
did的系数与标准误,最后分别绘制系数和t值的核密度估计图以及P值与系数的散点图。
3.2 代码实现
*==============================================================================*
* 双重差分法 | 安慰剂检验 *
*==============================================================================*
** Stata Version: 16 | 17
** 【文章首发】这篇文章首发于本人微信公众号『DMETP』,是两篇推文的合辑,欢迎关注!
**# 二、面板数据的安慰剂检验
*- 【原始数据来源】石大千, 丁海, 卫平, 刘建江. 智慧城市建设能否降低环境污染[J]. 中国工业经济, 2018(06): 117-135.
* 《中国工业经济》附件下载地址:http://ciejournal.ajcass.org/Magazine/show/?id=54281
*- 【加工数据来源】微信公众号『功夫计量经济学』2021.4.20推送文章“双重差分法(DID)安慰剂检验的做法:随机抽取500次”
* 微信公众号推文地址:https://mp.weixin.qq.com/s/06v6s90G1pp-yLju_yAy1Q
cd "C:\Users\KEMOSABE\Desktop\placebo_test\example"
**# 2.1 基础回归
use smart_city2018.dta, clear
global ctrlvars2 "lnrgdp lninno lnurb lnopen lnss"
reghdfe lnrso dudt $ctrlvars2 , absorb(id year) cluster(id)
*- 基础回归中核心变量dudt的真实系数与真实t值分别为:
*- 真实系数 = -0.1706
*- 真实t值 = -2.1245(可手动计算,即-0.1706 / 0.0803)
discard
**# 2.2 安慰剂检验
*- 思路:
*- a. 在原始数据集smart_city2018.dta中单独剔除变量id的样本数据
*- b. 将剔除出来的id随机打乱顺序,再将随机化的id合并至已被处理过的原始数据集中
*- c. 将随机化的treat与dt的交互项(did)放入回归方程中进行回归
*- d. 以上操作步骤重复1,000次
*- e. 单独提取出1,000次回归结果后did的系数与标准误,最后分别绘制did系数和t值的核密度估计图以及P值与系数的散点图
set seed 223 // 设置随机种子数
forvalue i = 1/1000 {
use smart_city2018.dta, clear
preserve
keep if year == 2005
gen randomvar = runiform()
sort randomvar
keep if id in 1/32
keep id
save id_random.dta, replace // 数据集仅保留随机化后的id
restore
merge m:1 id using id_random.dta // 将随机化id合并至原数据集
gen treat = (_merge == 3)
gen did = treat * dt
qui reghdfe lnrso did $ctrlvars2 , absorb(id year) cluster(id)
gen b_did = _b[did] // 提取单次回归后did的系数
gen se_did = _se[did] // 提取单次回归后did的标准误
keep b_did se_did
duplicates drop b_did, force
save placebo_`i'.dta, replace
}
erase id_random.dta
use placebo_1.dta, clear
forvalue k = 2/1000 {
append using placebo_`k'.dta // 将1,000次回归后did的系数和标准误纵向合并(append)至单独的数据集(placebo_1.dta)
erase placebo_`k'.dta
}
graph set window fontface "Times New Roman"
graph set window fontfacesans "宋体" // 设置图形输出的字体
gen tvalue = b_did / se_did
gen pvalue = 2 * ttail(e(df_r), abs(tvalue)) // 计算t值和P值
**# 2.2.1 系数
sum b_did, detail
twoway(kdensity b_did, ///
xline(`r(mean)', lpattern(dash) lcolor(black)) ///
xline(-0.1706 , lpattern(solid) lcolor(black)) ///
scheme(qleanmono) ///
xtitle("{stSans:系数}" , size(medlarge)) ///
ytitle("{stSans:核}""{stSans:密}""{stSans:度}", size(medlarge) orientation(h)) ///
saving(placebo_test_Coefficient2, replace)), ///
xlabel(, labsize(medlarge) format(%02.1f)) ///
ylabel(, labsize(medlarge) format(%02.1f)) // 绘制1,000次回归did的系数的核密度图
graph export "placebo_test_Coefficient2.png", replace // 导出为矢量图,方便论文中的图形展示;可改medlarge为large以加大字体
**# 2.2.2 P值
sum b_did, detail
twoway(scatter pvalue b_did, ///
msy(oh) mcolor(black) ///
xline(`r(mean)', lpattern(dash) lcolor(black)) ///
xline(-0.1706 , lpattern(solid) lcolor(black)) ///
yline( 0.1 , lpattern(shortdash) lcolor(black)) ///
scheme(qleanmono) ///
xtitle("{stSans:系数}" , size(medlarge)) ///
ytitle("{stSans:P}""{stSans:值}" , size(medlarge) orientation(h)) ///
saving(placebo_test_Pvalue2, replace)), ///
xlabel( , labsize(medlarge) format(%02.1f)) ///
ylabel(0(0.25)1, labsize(medlarge) format(%03.2f))
graph export "placebo_test_Pvalue2.png", replace
**# 2.2.3 t值
sum tvalue, detail
twoway(kdensity tvalue, ///
xline(`r(mean)', lpattern(dash) lcolor(black)) ///
xline(-2.1245 , lpattern(solid) lcolor(black)) ///
xline(-1.65 , lpattern(shortdash) lcolor(black)) ///
xline( 1.65 , lpattern(shortdash) lcolor(black)) ///
scheme(qleanmono) ///
xtitle("{stSans:t值}" , size(medlarge)) ///
ytitle("{stSans:核}""{stSans:密}""{stSans:度}", size(medlarge) orientation(h)) ///
saving(placebo_test_Tvalue2, replace)), ///
xlabel(, labsize(medlarge)) ///
ylabel(, labsize(medlarge) format(%02.1f)) // 绘制1,000次回归did的t值的核密度图
graph export "placebo_test_Tvalue2.png", replace
erase placebo_1.dta
3.3 运行结果与解读
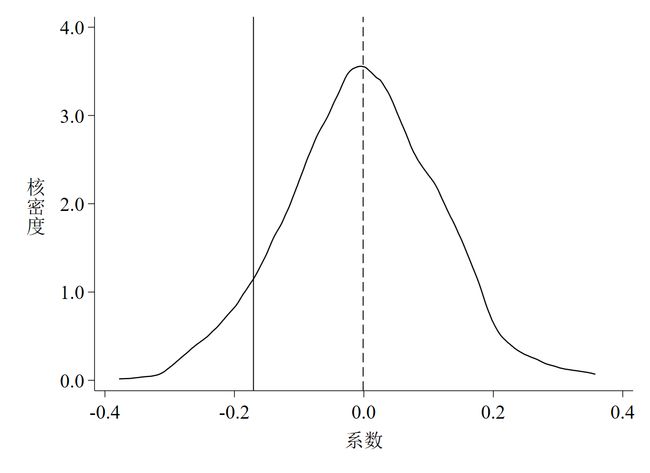
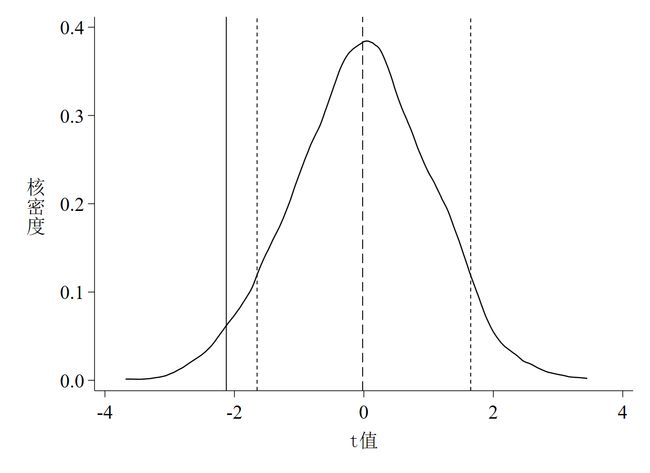
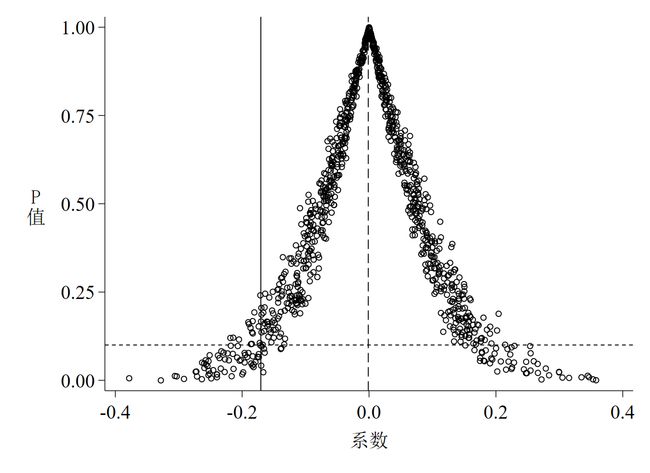
同样,以上代码的运行结果是3张图,如下图 4至图 6。
针对以上3张图,有如下几点解读。
-
第一,
图 4是随机化处理组后did项回归系数的核密度估计图,其中实线是基础回归估计出来的真实系数,虚线是1,000个“虚拟”系数的均值; -
第二,
图 5是t值的核密度估计图,其中实线是真实t值,虚线是均值,两根短虚线分别代表t = -1.65和t = 1.65(也即大样本下10%的显著性水平所对应的t值,t值的绝对值小于该数说明至少在10%的水平下不显著); -
第三,
图 6是P值的散点图,其中水平短虚线是P = 0.1,散点位于该虚线以下说明系数至少在10%的水平下显著,反之则不显著; -
第四,
图 4和图 5都说明了一个基本事实,那就是绝大多数系数和t值均集中分布在0附近,均值与真实值的距离较远,且绝大多数估计系数并不显著,这意味着智慧城市试点对环境污染治理的政策效应没有受到其他未被观测因素的影响。这个基本事实其实完全可以从P值的散点图(图 6)中得知,如散点集中分布在0附近,且远离其真实值,多数散点都位于虚线以上,同时说明在10%的水平下不显著,也就是说,P值散点图包含的信息其实更多更凝练。