机器学习简单概念和pytorch代码-2
机器学习简单概念和pytorch代码-2
学习率的选择和调校
特征工程
特征工程是数据预处理和分析过程中的一个关键步骤,主要用于机器学习和数据挖掘。它涉及到从原始数据中选择、修改和创建新的特征(即数据的属性或变量),以便提高模型的性能。在机器学习中,特征工程对于提高模型的准确性和效率至关重要。它包括以下几个主要步骤:
-
特征选择:从现有的特征集中选择最重要的特征,以减少维度并提高模型的效率。
-
特征提取:将原始数据转换为能够更好地表示问题的特征。这通常涉及到提取信息或减少维度,例如通过主成分分析(PCA)。
-
特征构造:基于现有数据创造新的特征,以揭示数据中的潜在模式或关系。
-
特征转换:对特征进行标准化、归一化或其他转换,使模型更容易处理。例如,将所有特征缩放到相同的范围。
-
特征编码:将非数值特征转换为数值格式,如将分类数据转换为独热编码(One-Hot Encoding)。
特征工程的主要目的是通过这些技术改进模型的性能,使其能够更有效地学习、理解和预测数据。在许多机器学习任务中,好的特征工程往往比选择高级模型更为重要。
多项式回归
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
# 检查CUDA是否可用,并设置device变量
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(torch.cuda.is_available())
# 创建数据集
x = torch.linspace(-3, 3, 100).unsqueeze(1).to(device) # x data (tensor), shape=(100, 1)
y = 1 + 2 * x + 3 * x ** 2 + torch.randn(x.size()).to(device) * 0.5 # noisy y data (tensor), shape=(100, 1)
# 定义多项式模型
class PolyModel(nn.Module):
def __init__(self):
super(PolyModel, self).__init__()
self.poly = nn.Linear(3, 1).to(device) # 一个线性层,输入特征为3(x, x^2, 常数项)
def forward(self, x):
poly_x = torch.cat([x ** 2, x, torch.ones_like(x)], dim=1) # 构造多项式特征
return self.poly(poly_x)
# 实例化模型、定义损失函数和优化器
model = PolyModel()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 训练模型
epochs = 1000
for epoch in range(epochs):
# 前向传播
y_pred = model(x)
# 计算损失
loss = criterion(y_pred, y)
# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (epoch+1) % 100 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
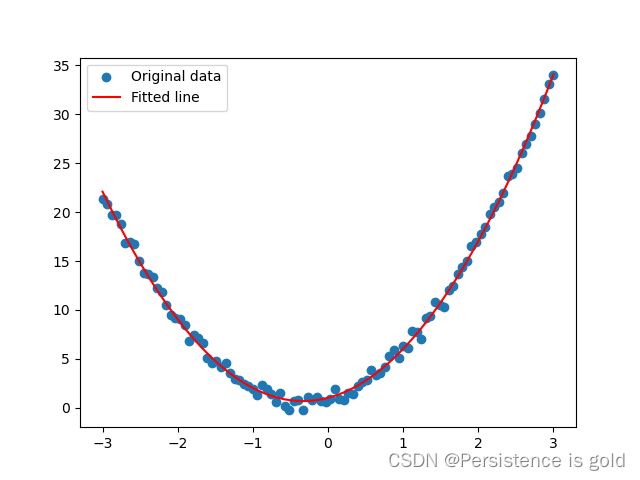
# 绘制结果
predicted = model(x).detach().cpu().numpy() # 将数据移回CPU来进行绘图
plt.scatter(x.cpu().numpy(), y.cpu().numpy(), label='Original data')
plt.plot(x.cpu().numpy(), predicted, label='Fitted line', color='r')
plt.legend()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error, r2_score
# 生成数据
np.random.seed(0)
x = np.linspace(-3, 3, 100)
y = 1 + 2 * x + 3 * x**2 + np.random.randn(*x.shape) * 0.5
x = x[:, np.newaxis] # 将x转换成二维数组,用于后续处理
# 创建多项式特征
poly_features = PolynomialFeatures(degree=2, include_bias=False)
x_poly = poly_features.fit_transform(x)
# 训练模型
model = LinearRegression()
model.fit(x_poly, y)
# 预测
y_pred = model.predict(x_poly)
# 计算评估指标
mse = mean_squared_error(y, y_pred)
r2 = r2_score(y, y_pred)
# 打印系数和评估指标
print("Model coefficients:", model.coef_)
print("Model intercept:", model.intercept_)
print("Mean squared error:", mse)
print("Coefficient of determination (R^2):", r2)
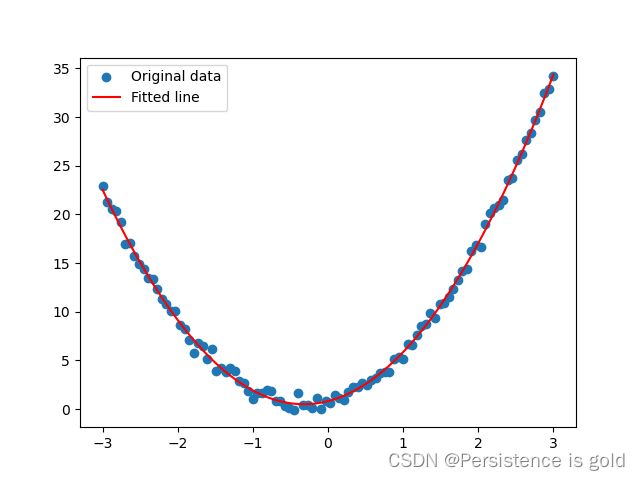
# 绘制结果
plt.scatter(x, y, label="Original data")
plt.plot(x, y_pred, color='red', label="Fitted line")
plt.legend()
plt.show()
logistic regression
Logistic回归是一种广泛用于分类任务的统计方法,尤其是在二分类问题中非常常见。尽管名称中包含“回归”,它实际上是一种分类算法,而不是回归算法。它的核心思想是利用logistic函数(或称为sigmoid函数)来估算概率,从而将线性回归模型的输出转换为介于0和1之间的概率值。
Logistic函数(Sigmoid函数)
Logistic回归的核心是logistic函数,也称为sigmoid函数。这个函数的公式是:
[ \sigma(z) = \frac{1}{1 + e^{-z}} ]
这里的(z)通常是特征和权重的线性组合,即(z = w_1x_1 + w_2x_2 + … + w_nx_n + b)。sigmoid函数将任何实数映射到(0, 1)区间,这使得它可以被解释为概率。
二分类
在二分类问题中,Logistic回归模型预测样本属于某个类别的概率。如果这个概率大于0.5,我们可以将样本分类为正类(通常标记为1);如果小于0.5,则分类为负类(标记为0)。
模型训练
Logistic回归模型通过最大化观测数据的似然函数来进行训练。这通常通过一种名为“逻辑损失”或“交叉熵损失”的损失函数来实现。模型训练的目标是找到一组权重,使得模型对训练数据的分类尽可能准确。
应用领域
Logistic回归由于其简单性和高效性,在许多领域都有广泛的应用,如医疗疾病预测、信用评分、市场营销响应预测等。它也是许多复杂分类算法和神经网络的基础。
扩展
虽然最常见的是二分类的Logistic回归,但它也可以被扩展到多分类问题(例如,使用softmax函数代替sigmoid函数)。在多分类Logistic回归中,模型会估计一个样本属于每个类别的概率,并将其分类到概率最高的类别。
# 导入必要的库
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
# 设置随机种子,以便结果可复现
torch.manual_seed(0)
# 检查CUDA是否可用,并设置device变量
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 创建数据集
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, n_informative=2,
random_state=1, n_clusters_per_class=1)
# 转换数据类型
features = torch.tensor(X, dtype=torch.float32).to(device)
labels = torch.tensor(y, dtype=torch.float32).view(-1, 1).to(device)
# 定义Logistic回归模型
class LogisticRegressionModel(nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = nn.Linear(2, 1)
def forward(self, x):
y_pred = torch.sigmoid(self.linear(x))
return y_pred
# 实例化模型,并移动到GPU(如果可用)
model = LogisticRegressionModel().to(device)
# 损失函数和优化器
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 训练模型
epochs = 1000
for epoch in range(epochs):
# 前向传播
y_pred = model(features)
# 计算损失
loss = criterion(y_pred, labels)
# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (epoch+1) % 100 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
# 绘制结果(注意:绘图部分需要在CPU上进行)
features_cpu = features.cpu()
labels_cpu = labels.cpu()
model_cpu = model.cpu()
def plot_decision_boundary(X, y):
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))
# 预测整个网格
Z = model(torch.tensor(np.c_[xx.ravel(), yy.ravel()], dtype=torch.float32))
Z = Z.view(xx.shape).detach().numpy()
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Logistic Regression Decision Boundary')
plot_decision_boundary(features_cpu.numpy(), labels_cpu.numpy())
plt.show()
决策边界(Decision Boundary)
决策边界(Decision Boundary)是在分类问题中用来区分不同类别的边界。在一个分类模型中,决策边界定义了输入空间中一组点,这些点被模型划分为不同的类别。根据模型的复杂性和特征的数量,决策边界可以是直线、曲线或多维曲面。
在不同类型的模型中的决策边界
-
线性模型:在线性模型(如线性回归、Logistic回归)中,决策边界是一个直线(在二维空间)或一个平面(在三维空间)。例如,在二维空间中,Logistic回归的决策边界可能是一条直线,将数据点分为两部分,一部分属于正类(class 1),另一部分属于负类(class 0)。
-
非线性模型:在非线性模型中(如决策树、支持向量机(SVM)等),决策边界可能是曲线或复杂的形状。这使得模型能够更好地捕捉数据中的复杂模式。
决策边界的作用
-
分类:决策边界是用来确定新的数据点应该被分配到哪个类别的基础。数据点的位置相对于决策边界决定了其分类。
-
模型解释:通过可视化决策边界,我们可以对模型的行为有一个直观的理解。例如,决策边界可以帮助我们理解模型是否过拟合或欠拟合。
-
特征重要性:在某些情况下,决策边界的形状和位置可以反映出不同特征对模型决策过程的影响。
可视化决策边界
在二维空间中,决策边界通常可以通过绘制图形直观地展示。例如,你可以在二维散点图中画出分类模型的决策边界,以展示模型是如何将数据点分为不同类别的。在更高维的空间中,决策边界的可视化变得更加复杂,通常需要使用降维技术或选择特定的两个维度进行可视化。
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
# 设置随机种子
torch.manual_seed(0)
# 创建一个更复杂的数据集
X, y = make_moons(n_samples=100, noise=0.2, random_state=0)
X = torch.tensor(X, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.float32).view(-1, 1)
# 定义GPU设备(如果可用)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 将数据移动到GPU(如果可用)
X, y = X.to(device), y.to(device)
# 定义模型
class ComplexModel(nn.Module):
def __init__(self):
super(ComplexModel, self).__init__()
self.fc1 = nn.Linear(2, 10) # 输入层到隐藏层
self.fc2 = nn.Linear(10, 10) # 隐藏层
self.fc3 = nn.Linear(10, 1) # 隐藏层到输出层
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
return torch.sigmoid(self.fc3(x))
# 实例化模型并移动到GPU(如果可用)
model = ComplexModel().to(device)
# 损失函数和优化器
criterion = nn.BCELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
# 训练模型
epochs = 1000
for epoch in range(epochs):
y_pred = model(X)
loss = criterion(y_pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (epoch+1) % 100 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
# 绘制决策边界
def plot_decision_boundary(model, X, y):
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))
# 预测整个网格
Z = model(torch.tensor(np.c_[xx.ravel(), yy.ravel()], dtype=torch.float32))
Z = Z.view(xx.shape).detach().numpy()
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Logistic Regression Decision Boundary')
# 绘制(注意需要将数据和模型移到CPU)
plot_decision_boundary(model.cpu(), X.cpu(), y.cpu())
plt.show()

使用平方误差函数在逻辑回归中产生的成本函数效果不好
逻辑回归的损失函数
过拟合
过拟合(Overfitting)是机器学习中一个常见的问题,它发生在模型对训练数据学得“太好”时,以至于它过度捕捉了训练数据中的噪声和细节,而不能很好地泛化到新的、未见过的数据上。简而言之,过拟合是模型在训练数据上表现出色,但在验证数据或测试数据上表现不佳的情况。
过拟合的特征和原因
- 高方差:过拟合模型通常表现出高方差,即模型对训练数据的小变动非常敏感。
- 模型过于复杂:如果模型比需要解决的问题复杂得多,它可能会学到数据中的随机噪声而不是潜在的模式。
- 训练时间过长:特别是在神经网络中,如果训练时间过长,模型可能开始记忆训练数据,而不是学习泛化的特征。
- 数据量不足:如果训练数据不够多,模型可能无法学习到足够泛化的特征。
如何检测过拟合
- 性能差异:一个明显的过拟合迹象是训练误差远远小于验证误差。
- 学习曲线:绘制训练误差和验证误差随时间的变化,如果训练误差持续下降,而验证误差开始增加,这可能是过拟合的迹象。
如何防止过拟合
- 增加数据量:更多的数据可以帮助模型学习更泛化的特征。
- 数据增强:在图像处理中,通过旋转、缩放、裁剪等方式增强数据可以增加数据的多样性。
- 减少模型复杂度:选择更简单的模型或减少模型中的参数数量。
- 正则化:例如L1或L2正则化,可以限制模型权重的大小,防止模型变得过于复杂。
- 早期停止:在训练过程中,一旦验证误差开始增加,立即停止训练。
- 交叉验证:使用交叉验证来更好地估计模型在新数据上的性能。
- Dropout:在神经网络中,Dropout可以随机地暂时“丢弃”一部分神经元,防止网络对特定的特征过度依赖。
总之,过拟合是一个需要在模型设计和训练过程中持续关注的问题,通过上述策略可以有效地减少过拟合的风险,提高模型的泛化能力。
特性选择
特征选择(Feature Selection)是在构建机器学习模型的过程中选择最重要的特征(输入变量)的过程。这是机器学习的关键步骤之一,因为选择正确的特征集合可以提高模型的性能,同时减少计算成本和模型复杂度。
特征选择的重要性
- 提高性能:去除不相关或冗余的特征可以提高模型的准确性。
- 减少过拟合:减少特征数量可以降低模型复杂度,从而减少过拟合的风险。
- 减少训练时间:较少的特征意味着模型训练所需的计算量较小。
- 提高模型可解释性:具有较少特征的模型通常更容易解释和理解。
特征选择的方法
-
过滤方法(Filter Methods):这些方法在训练模型之前选择特征。它们通常基于统计测试(如相关性或卡方测试)来评估特征的重要性。
-
包装方法(Wrapper Methods):这些方法将特征选择视为搜索问题,其中不同的特征组合被训练和评估。例子包括向前选择(Forward Selection)、向后消除(Backward Elimination)和递归特征消除(Recursive Feature Elimination, RFE)。
-
嵌入方法(Embedded Methods):这些方法在模型训练过程中进行特征选择。例如,使用L1正则化的线性模型(如Lasso)可以在训练过程中选择特征。
-
维度缩减:虽然不严格是特征选择(因为它创建新的特征组合),方法如主成分分析(PCA)和线性判别分析(LDA)可以减少特征空间的维度。
特征选择的注意事项
- 数据泄露:在特征选择过程中应避免使用未来数据,以防止数据泄露。
- 特征重要性的依赖性:某些特征选择方法可能依赖于特定类型的模型。
- 特征间的相互作用:在某些情况下,单独的特征可能不重要,但当与其他特征组合时却很重要。
总之,特征选择是一个关键的步骤,可以显著提高机器学习模型的性能和效率。正确的特征选择不仅可以提高模型的精确度,还可以减少计算成本和提高模型的可解释性。
进行正规化防止过拟合
在PyTorch中实现带有正则化的线性回归并使用GPU加速,可以通过在损失函数中加入一个正则项来完成。在机器学习中,常见的正则化方法有L1正则化(也称为Lasso回归)和L2正则化(也称为Ridge回归)。以下是一个使用L2正则化(Ridge回归)的线性回归模型的示例:
- 导入必要的库:导入PyTorch及相关库。
- 创建数据集:生成一些用于线性回归的合成数据。
- 定义线性回归模型:创建一个简单的线性回归模型。
- 定义损失函数和正则化:定义均方误差损失并加入L2正则化。
- 选择优化器:选择一个优化器,如SGD或Adam。
- 在GPU上训练模型:如果可用,利用GPU进行训练。
示例代码
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
# 设置随机种子以确保结果可重现
torch.manual_seed(0)
# 创建数据集
x = torch.linspace(-3, 3, 100).unsqueeze(1)
y = 1 + 2 * x + torch.randn(x.size()) * 0.5
x, y = x.to('cuda'), y.to('cuda') # 移动数据到GPU
# 定义线性回归模型
class LinearRegressionModel(nn.Module):
def __init__(self):
super(LinearRegressionModel, self).__init__()
self.linear = nn.Linear(1, 1)
def forward(self, x):
return self.linear(x)
# 实例化模型并移动到GPU
model = LinearRegressionModel().to('cuda')
# 损失函数(均方误差)和L2正则化
def criterion(output, target, model, reg_lambda):
loss = nn.MSELoss()(output, target)
l2_reg = torch.tensor(0.).to('cuda')
for param in model.parameters():
l2_reg += torch.norm(param)
return loss + reg_lambda * l2_reg
# 优化器
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 训练模型
epochs = 1000
reg_lambda = 0.1 # L2正则化系数
for epoch in range(epochs):
# 前向传播
y_pred = model(x)
# 计算损失
loss = criterion(y_pred, y, model, reg_lambda)
# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (epoch+1) % 100 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
# 绘制结果(注意:需要将数据移到CPU)
predicted = model(x).detach().cpu()
plt.scatter(x.cpu().numpy(), y.cpu().numpy(), label='Original data')
plt.plot(x.cpu().numpy(), predicted.numpy(), label='Fitted line', color='r')
plt.legend()
plt.show()
在这个代码示例中,我们使用均方误差损失函数,并添加了一个L2正则化项。L2正则化项是模型参数的平方和,乘以一个正则化系数reg_lambda。这种正则化有助于防止模型过拟合,使得模型参数不会变得过大。
请确保你的环境已经安装了PyTorch,并且你的机器具有NVIDIA GPU以及相应的CUDA支持。如果没有GPU,这段代码仍然可以在CPU上运行,只需将所有.to('cuda')调用改为.to('cpu')或直接删除这些调用即可。

在PyTorch中实现带有正则化的逻辑回归并使用GPU加速,可以通过在损失函数中加入一个正则项来完成。以下是一个使用L2正则化的逻辑回归模型的示例:
- 导入必要的库:导入PyTorch及相关库。
- 创建数据集:生成一些用于逻辑回归的合成数据。
- 定义逻辑回归模型:创建一个简单的逻辑回归模型。
- 定义损失函数和正则化:定义二元交叉熵损失并加入L2正则化。
- 选择优化器:选择一个优化器,如SGD或Adam。
- 在GPU上训练模型:如果可用,利用GPU进行训练。
示例代码
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import make_classification
import numpy as np
import matplotlib.pyplot as plt
# 设置随机种子以确保结果可重现
torch.manual_seed(0)
# 创建数据集
X, y = make_classification(n_samples=100, n_features=2, n_classes=2, n_clusters_per_class=1, random_state=0)
X = torch.tensor(X, dtype=torch.float32).to('cuda') # 使用GPU
y = torch.tensor(y, dtype=torch.float32).view(-1, 1).to('cuda') # 使用GPU
# 定义逻辑回归模型
class LogisticRegressionModel(nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = nn.Linear(2, 1)
def forward(self, x):
return torch.sigmoid(self.linear(x))
# 实例化模型并移动到GPU
model = LogisticRegressionModel().to('cuda')
# 损失函数(二元交叉熵)和L2正则化
def criterion(output, target, model, reg_lambda):
loss = nn.BCELoss()(output, target)
l2_reg = torch.tensor(0.).to('cuda')
for param in model.parameters():
l2_reg += torch.norm(param)
return loss + reg_lambda * l2_reg
# 优化器
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 训练模型
epochs = 1000
reg_lambda = 0.1 # L2正则化系数
for epoch in range(epochs):
# 前向传播
y_pred = model(X)
# 计算损失
loss = criterion(y_pred, y, model, reg_lambda)
# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (epoch+1) % 100 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
# 绘制结果(注意:需要将数据移到CPU)
predicted = model(X).detach().cpu()
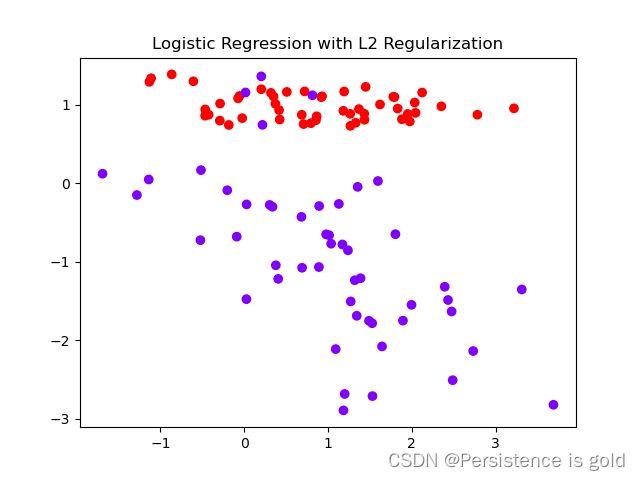
plt.scatter(X.cpu()[:, 0], X.cpu()[:, 1], c=y.cpu().view(-1), cmap='rainbow')
plt.title('Logistic Regression with L2 Regularization')
plt.show()
在这个代码示例中,我们使用二元交叉熵损失函数,并添加了一个L2正则化项。L2正则化项是模型参数的平方和,乘以一个正则化系数reg_lambda。这种正则化有助于防止模型过拟合,使得模型参数不会变得过大。
请确保你的环境已经安装了PyTorch,并且你的机器具有NVIDIA GPU以及相应的CUDA支持。如果没有GPU,这段代码仍然可以在CPU上运行,只需将所有.to('cuda')调用改为.to('cpu')或直接删除这些调用即可。