学习周报2.26

---

前言

This week,I read an article about daily streamflow prediction.This study shows the results of an in-depth comparison between two different daily streamflow prediction models: a novel simpler model based on the stacking of the Random Forest and Multilayer Perceptron algorithms, and a more complex model based on bi-directional Long Short Term Memory (LSTM) networks.The two models show comparable forecasting capabilities.In addition，I learn the attention mechanism and the calculation process through some examples.
本周阅读文献，文献主要研究对比了两种河流日流量预测模型，基于随机森林和多层感知机算法叠加的简单模型以及基于双向长短时记忆网络的复杂模型，通过研究发现两种模型预测能力基本相当。另外，学习了attention机制，通过例子了解attention的计算过程。

---

文献阅读

题目：Stacked machine learning algorithms and bidirectional long short-term memory networks for multi-step ahead streamflow forecasting: A comparative study

作者：Francesco Granata, Fabio Di Nunno, Giovanni de Marinis

摘要

河流流量的预测是防洪和优化水资源管理的一项基本任务。但由于流域特征，水文过程和气候因素的高不确定性，导致预测过程很困难。本研究对比了两种不同的日流量预测模型：基于随机森林和多层感知机算法叠加的简单模型以及基于双向长短时记忆网络的复杂模型。结果表明两种模型预测能力相当，堆叠模型在预测峰值流速方面优于双向LSTM网络模型，但在预测低流速方面不太准确。

随着模型日益复杂，依赖大量的参数和输入数据，而这些参数和输入数据往往不容易获得，导致模型计算成本大。因此，建立基于少量输入变量和少量参数的简单模型将非常有用，其特点是具有与最近开发的复杂模型相当的预测能力。因此，建立基于少量输入变量和少量参数的简单模型将非常有用，其特点是具有与最近开发的复杂模型相当的预测能力，并试图回答以下问题：
1.这种新颖的集成模型能否提供与更复杂的深度学习算法（如双向LSTM）在日常流量预测中相当的结果？
2.随着预测范围的增加，模型的性能如何变化？

堆叠是一种集成机器学习技术，通过元分类器组合多个分类或回归模型。基于整个训练数据集开发单个分类或回归模型，然后根据融合中各个模型的输出（元特征）拟合元分类器。通过堆叠随机森林（RF）和多层感知器（MLP）算法获得集成模型。弹性网络（EN）算法被用作元学习器。

方法

随机森林和多层感知器的堆叠

随机森林（RF）和多层感知器（MLP）被用作基础学习器，而弹性网络（EN）算法则被选为元分类器来开发堆叠预测模型。

RF 是一种集成预测算法，通过组合一组单独的回归树来提供目标变量的单个值。每个单独的回归树的特征是根节点，其中包括训练数据集，内部节点指定输入变量的条件，叶子表示分配给目标变量的实际值。回归树模型是通过将输入数据集递归细分为子集来开发的。多变量线性回归模型在每个子集中提供预测。在树的生长过程中，每个分支被划分为较小的分区，评估每个字段上所有可能的细分，并在每个阶段找到拆分为两个不同的分区，从而最小化最小二乘偏差：
N（t） 是节点 t 中的单元数，ym是第 i 个单位中目标变量的值，并且ym是节点 t 中目标变量的平均值。
R（t）给出了每个节点中“不纯度”的估计值。

MLP是前馈人工神经网络.MLP 至少由三层节点组成：输入层、隐藏层和输出层。输入层包括接收输入数据的节点。隐藏层中的每个节点使用加权线性和处理前一层的值，然后是非线性激活函数。最后一个隐藏层将值传递给输出层，输出层将它们转换为最终计算值。算法训练使用反向传播技术。
本研究中使用的神经网络有 1 个隐藏层。选择sigmoid作为激活函数，选择平方误差作为损失函数。

弹性网络是两种最常用的线性回归正则化变体的组合：LASSO（最小绝对收缩和选择运算符）和Ridge方法。LASSO，也称为 L1 正则化，通过对普通最小二乘 （OLS） 回归引入绝对惩罚来追求选择最解释变量的目标。Ridge正则化，称为 L2 正则化，也在 OLS 公式中引入了惩罚，惩罚平方权重而不是绝对权重。通过这种方式，大权重会受到相当大的惩罚，而许多小权重分布在特征谱中。
双向长短期记忆网络
LSTM网络已被证明在解决涉及水文量时间序列的复杂问题方面特别有效。LSTM 层由一组以循环方式连接的内存块组成。它们中的每一个都包含一个或多个反复连接的存储单元和三个乘法单元：输入、输出和遗忘门，允许对单元进行读取、写入和重置操作。
LSTM网络中的每个存储单元通过隐藏状态（ht），称为短期记忆和细胞状态（Ct），称为长期记忆。LSTM单元的代表性方程可以采用以下形式提出：

与标准LSTM相比，双向LSTM具有数据在正向和反向方向上同时处理。时间步长 t 的双向 LSTM 网络的输出由两个单独的隐藏级别的组合提供，其中每个隐藏级别代表一个训练序列，对应于正向和反向。因此，双向 LSTM 可以比标准 LSTM 更好地学习输入序列的未来和过去信息。

评估指标
使用四种不同的估值指标来估计预测模型的准确性：决定系数、均方根误差、平均方向精度和平均绝对百分比误差。
决定系数（R2） 是回归模型中的统计度量，它通过范围 [0， 1] 中的数字评估模型与数据的拟合优度。

均方根误差 （RMSE） 是绝对误差的度量，其中偏差被平方以防止正值和负值相互抵消。此外，该度量值放大了更大价值的误差，这一特征会惩罚具有最显着误差的模型。

其中 N 是时间序列中预测数据的总量。
平均方向精度 （MDA） 将预测方向（向上或向下）与实际实现的方向进行比较，提供预测模型可以检测到时间序列正确方向的概率。

其中 sgn（·） 是符号函数，而 1 是指标函数。

平均绝对百分比误差 （MAPE） 是预测模型的绝对百分比误差的平均值，其中误差定义为实际值减去预测值。

结果

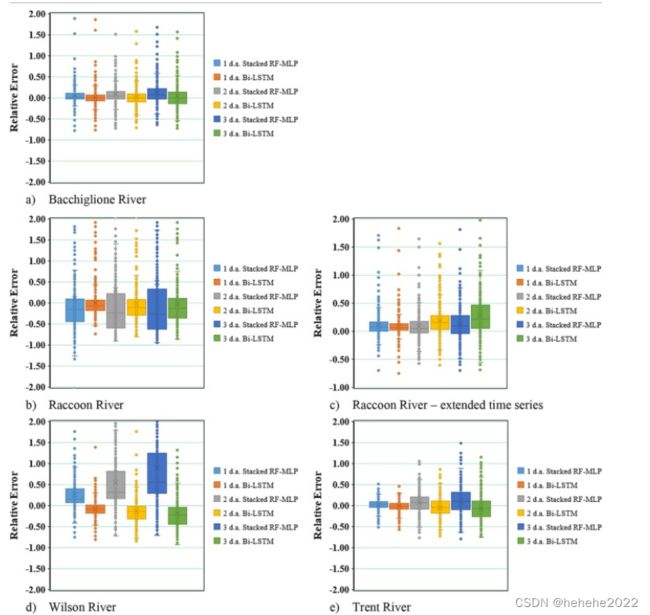
本研究发现，基于RF和MLP算法堆叠的溪流预测模型可以产生与基于Bi-LSTM的更复杂的模型相当的结果。堆叠模型的最大优势在于计算时间，大约是Bi-LSTM模型所需计算时间的10%。

深度学习

Encoder-Decoder（编码-解码）

Encoder-Decoder是一个模型构架，是一类算法统称，并不是特指某一个具体的算法，在这个框架下可以使用不同的算法来解决不同的任务。首先，编码（encode）由一个编码器将输入序列转化成一个固定维度的稠密向量，解码（decode）阶段将这个激活状态生成目标译文。

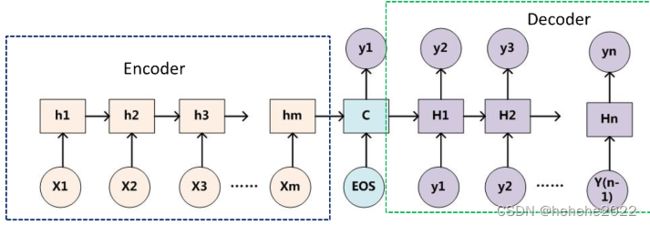
说明：
不论输入和输出的长度是什么，中间的“向量c”长度都是固定的（这是它的缺陷所在）。根据不同的任务可以选择不同的编码器和解码器（例如，CNN、RNN、LSTM、GRU等）
Encoder
对于输入序列x=(x1,…,xT),其会将输入序列如图所示编码成一个context vector c ，encoder一般使用RNN，在RNN中，当前时间的隐藏状态是由上一时间的状态和当前时间输入决定的，也就是

Decoder
一般其作用为在给定context vector c和所有已预测的词 {y1,…,yt−1}去预测 yt，t时刻隐藏状态st为：

信息丢失的问题

通过上文可以知道编码器和解码器之间有一个共享的向量（上图中的向量c），来传递信息，而且它的长度是固定的。这会产生一个信息丢失的问题，编码器要将整个序列的信息压缩进一个固定长度的向量中去。但是这样做有两个弊端，一是语义向量无法完全表示整个序列的信息，还有就是先输入的内容携带的信息会被后输入的信息稀释掉，或者说，被覆盖了。使得在解码的时候一开始就没有获得输入序列足够的信息，那么解码的准确度也会低。为了解决这些缺陷，又引入了Attention机制，Attention模型的特点是Encoder不再将整个输入序列编码为固定长度的中间向量，而是编码成一个向量序列。Encoder 将句子编码成一个向量序列，而不是一个向量，然后再预测翻译单词的每一步选择这些向量的子集作为注意力向量输入到 Decoder 中。

Attention与传统的Seq2Seq模型主要有以下两点不同：
1.encoder提供了更多的数据给到decoder，encoder会把所有的节点的hidden state提供给decoder，而不仅仅只是encoder最后一个节点的hidden state。
2.decoder并不是直接把所有encoder提供的hidden state作为输入，而是采取一种选择机制，把最符合当前位置的hidden state选出来。

确定哪一个hidden state与当前节点关系最为密切，计算每一个hidden state的分数值，对每个分数值做一个softmax的计算，这能让相关性高的hidden state的分数值更大，相关性低的hidden state的分数值更低。

把每一个encoder节点的hidden states的值与decoder当前节点的上一个节点的hidden state相乘，如上图，h1、h2、h3分别与当前节点的上一节点的hidden state进行相乘(如果是第一个decoder节点，需要随机初始化一个hidden state)，也就是计算每一个输入位置j的hidden vector与当前输出位置的关联性similarity（st-1,hj）,相似度的计算方式有很多，最后会获得三个值，这三个值就是上文提到的hidden state的分数，这个数值对于每一个encoder的节点来说是不一样的，把该分数值进行softmax计算，得到attention的分布，计算之后的值就是每一个encoder节点的hidden states对于当前节点的权重，把权重与原hidden states相乘并相加，得到的结果即是当前节点的hidden state。Atttention的关键就是计算这个分值。

Attention机制

Attention机制从上文讲述例子中的Encoder-Decoder框架中剥离，Attention函数的本质可以被描述为一个查询（query）到一系列（键key-值value）对的映射。在计算attention时主要分为三步：
第一步是将query和每个key进行相似度计算得到权重，常用的相似度函数有点积，拼接，感知机等；
第二步一般是使用一个softmax函数对这些权重进行归一化，我们将 αi 称之为注意力分布（概率分布）；
最后将权重和相应的键值value进行加权求和得到最后的attention。目前在NLP研究中，key和value常常都是同一个，即key=value。

---

总结

带有Attention的Encoder-Decoder网络的迭代过程：
1.Encoder网络按照原来的方法计算出 h1,h2…ht;
2.计算Decoder网络，对于第 K个输出词语，先计算出得到Ck所需要的h1,h2…ht的权重ak，ak的计算如上述公式所示，再计算Ck=ak1h1+ak2h2…;
3.将Hk-1,yk-1,Ck带入f(Hk-1,yk-1,Ck)计算Hk，再把Hk带入网络计算yk。