【leetcode 447. 回旋镖的数量】审慎思考与推倒重来

447. 回旋镖的数量

题目描述

给定平面上 **n **对 互不相同 的点 points ，其中 points[i] = [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 ，其中 i 和 j 之间的距离和 i 和 k 之间的欧式距离相等（需要考虑元组的顺序）。

返回平面上所有回旋镖的数量。

原始思路

根据题目描述，所谓回旋镖就是对于一个点i，存在另外两个点到该点的距离相等。

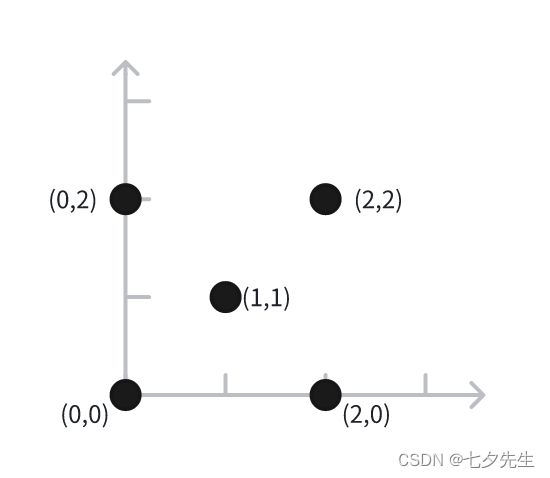
以下图为例，点(0,0)到(0,2)、(2,0)的距离是相通的，这就是一个回旋镖。同样的，点(2,2)与(0,2)、(2,0)也构成一个回旋镖。

大概理解题目的含义后，最直接的想法就是遍历，通过三重遍历分辨判断是否为回旋镖，最后的统计数目就是需要的结果。代码实现如下：

class Solution {
private:
    // 判断点i与点j、点k是否构成回旋镖
    // ps：这里省略了开方运算
    bool isBoomeranges(vector& i, vector& j, vector& k) {
        return ((j[1] - i[1]) * (j[1] - i[1])) + ((j[0] - i[0]) * (j[0] - i[0])) == ((k[1] - i[1]) * (k[1] - i[1])) + ((k[0] - i[0]) * (k[0] - i[0]));
    }
public:
    int numberOfBoomerangs(vector>& points) {
        int res = 0;
        int pointNum = points.size();
        for(int i = 0;i < pointNum;++i) {
            for(int j = 0;j < pointNum;++j) {
                for(int k = 0;k < pointNum;++k) {
                    if(i == j || i == k || j == k) {
                        // 同一个点不算
                        continue;
                    }
                    if(isBoomeranges(points[i], points[j], points[k])) {
                        ++res;
                    }
                }
            }
        }
        return res;
    }
};

三重循环，不出意外地超时了……

试图挽回，空间换时间

三重循环每次都要计算距离，肯定是做了很多重复运算的，或许可以用空间换时间，

尝试代码如下：

class Solution {
public:
    int numberOfBoomerangs(vector>& points) {
        int res = 0;
        int pointNum = points.size();
        vector> dis(pointNum, vector(pointNum, 0)); // 记录点与点之间的“距离”
        for(int i = 0;i < pointNum;++i) {
            for(int j = i + 1;j < pointNum;++j) {
                dis[j][i] = dis[i][j] = ((points[j][1] - points[i][1]) * (points[j][1] - points[i][1])) + ((points[j][0] - points[i][0]) * (points[j][0] - points[i][0]));
            }
        }
        for(int i = 0;i < pointNum;++i) {
            for(int j = 0;j < pointNum;++j) {
                for(int k = 0;k < pointNum;++k) {
                    if(i == j || i == k || j == k) {
                        continue;
                    }
                    if(dis[i][j] == dis[i][k]) {
                        ++res;
                    }
                }
            }
        }
        return res;
    }
};

结果从通过25个测试用例提升到通过28个。改善了，但又没完全改善。

到这里，意识到应该是解决方案本身的时间复杂度$O(n^3)$就太高了。

回归本源，方法为王

虽然上面的思路简单易懂，但也把我带入“歧途”，没有深入审视题目中的含义。

所以遍历思路走到尽头后，不得不重新审视题目。

三重循环中有很多计算是重复的，还是以开头的例子做讲解，对于点(1,1)，它需要分别判断：

1. 与(0,0)、(0,2)是否构成回旋镖
2. 与(0,0)、(2,2)是否构成回旋镖
3. 与(0,0)、(2,0)是否构成回旋镖
4. 与(0,2)、(0,0)是否构成回旋镖
5. 与(0,2)、(2,2)是否构成回旋镖
6. 与(0,2)、(2,0)是否构成回旋镖
7. 与(2,2)、(0,0)是否构成回旋镖
8. 与(2,2)、(0,2)是否构成回旋镖
9. 与(2,2)、(2,0)是否构成回旋镖
10. 与(2,0)、(0,0)是否构成回旋镖
11. 与(2,0)、(0,2)是否构成回旋镖
12. 与(2,0)、(2,2)是否构成回旋镖

在这个过程中，(1,1)和(0,0)、(0,2)、(2,2)、(2,0)的距离，分别被算了6遍。

但实际上，(1,1)到这四个点的距离都是相同的，任取两个点都能和(1,1)构成回旋镖，再加上顺序敏感的题目要求（既$[(1,1),(0,0),(0,2)]$与$[(1,1),(0,2),(0,0)]$是两个回旋镖），利用排列数计算就能替代多余计算。

所以，对于某个点i，只需统计其他点与i之间的距离，然后利用排列数就可以计算出回旋镖的数目。
比如上面的例子中，距离为$\sqrt{2}$的点对有4个，那么$A_4^2=4\times 3=12$。

算法步骤：

1. 遍历所有点
2. 对于某个点i，统计与其他点的距离长度
3. 对每个距离长度的数目，计算排列数
4. 所有排列数之和即为答案

class Solution {
private:
    int distance(const vector& p1, const vector& p2) {
        // 计算两点之间的“距离”
        return (p1[0] - p2[0]) * (p1[0] - p2[0]) + (p1[1] - p2[1]) * (p1[1] - p2[1]);
    }
public:
    int numberOfBoomerangs(vector>& points) {
        int res = 0;
        int pointNum = points.size();
        for(int i = 0;i < pointNum;++i) {
            // 遍历所有点
            unordered_map disNumMp;
            for(int j = 0;j < pointNum;++j) {
                // 统计该点与其他之间距离长度的数目
                // 只有该点自己到自己的长度为0，所以0对应的数目一定为0，不影响最终结果计算，无需剔除
                ++disNumMp[distance(points[i], points[j])];
            }
            for(auto it = disNumMp.begin();it != disNumMp.end();++it) {
                // 计算排列数
                res += (it->second * (it->second - 1));
            }
        }
        return res;
    }
};

小感悟

有些时候，人容易对一开始选择的路径产生依赖，不推倒重来就难以跳脱。

审慎的思考和选择或许可以避免弯路，但更多时候还是要走到南墙才能意识到选择的对错。

所以，要有审慎选择的过程，也要有推倒重来的勇气！