算法程序设计实验报告
多种方法解决算法问题
- 题目一
-
- 方法一：快速排序
- 方法二：直接插入排序
- 方法三：选择法排序
- 方法四：冒泡排序
- 题目二
-
- 方法一：冒泡排序
- 方法二：堆排序
- 方法三：分治策略
- 方法四：二路归并排序
- 题目三
-
- 方法一：穷举法
- 方法二：动态规划
- 方法三：闫氏DP分析法
- 题目四
-
- 方法一：蛮力法
- 方法二：分治法
- 方法三：动态规划法
- 四、 设计技巧及体会
题目一
题目1：设A是n个非0实数构成的数组，设计一个算法重新排列数组中的数，使得负数都排在正数前面，要求用多种算法实现，并保证至少算法中有一种算法使用O(n)的时间和O(1)的空间。
方法一：快速排序
1.原理：
数列中挑出一个元素，称为 “基准”（pivot）;重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；
2.代码：
import pandas as pd
import numpy as np
import math
import copy
import time
def reorder(mylist, start, end):
# 若选其他元素作为pivot，下面的while内容需要相应更改
pivot = 0
left = start
right = end
while left < right:
while left < right and mylist[left] > pivot:
left += 1
while left < right and mylist[right] < pivot:
right -= 1
if left != right:
mylist[left], mylist[right] = mylist[right], mylist[left]
mylist[end], mylist[left] = mylist[left], pivot
return left
#读取文件中的数据
df=open("E:\\研一第一学期\\算法\\100万.txt")
list1=[]
for line in df:
list1.append([int(x) for x in line.split(" ")])
time_start=time.time()#开始计时
reorder(list1[0],0,len(list1[0])-1)
time_end=time.time() #结束计时
time_c=time_end-time_start
print("reorder所用时间：",time_c,'s')
#输出排序后的数据到文件
f=open("E:\\研一第一学期\\算法\\out0.txt","w")
for row in list1:
print(row ,file=f)
3.运行结果：
方法二：直接插入排序
1.原理：
将待排序序列分为两部分，一部分有序一部分无序；
第一个元素为有序序列，从第二个元素到最后为无序序列 ；
将无序序列中每一个元素依次插入到有序序列的合适位置–从小到大（从大到小）合适的位置：待排序元素大于或等于（小于）该元素
2.代码：
#include
void InsertSort(int array[],int len){
int i,j;
//第一个for循环 遍历无序序列
for(i=1;i=0;j--){ //将待排序元素依次和有序序列中的元素比较
//待排序元素 小于 有序序列中当前元素时 将该元素后移
array[j+1] = array[j];
}
array[j+1] = tem; //待排序元素 大于 有序序列最后一个元素 直接将该元素插入到有序序列最后
}
}
int main(){
printf("Please input the number of arrays:\n");
int n;
scanf("%d",&n);
printf("Please input the elements:\n");
int a[n],i;
for(i=0;i 3.运行结果：
方法三：选择法排序
1.原理：
(1）首先通过n-1次比较，从n个数中找出最小的， 将它与第一个数交换—第一趟选择排序，结果最小的数被安置在第一个元素位置上
（2）再通过n-2次比较，从剩余的n-1个数中找出关键字次小的
记录，将它与第二个数交换—第二趟选择排序
（3）重复上述过程，共经过n-1趟排序后，排序结束
2.代码：
#include
int main()
{
printf("Please input the number of arrays:\n");
int n;
scanf("%d",&n);
printf("Please input the elements:\n");
int a[n];
int Pos, tmp, i, j;
for(i=0;i 3.运行结果：
方法四：冒泡排序
1.原理：
(1）第一趟扫描：从i=1开始，依次比较A[i]与A[i+1] ，若为逆序(A[i]>A[i+1])，
则交换其值；依次类推，直至第n-1个数和第n个数比较为止——
第一趟扫描使最大的数被安置在第n个元素位置上。
（2）对前n-1个数进行第二趟扫描，结果使次最大的数被安置在第n-1个元素位置。
（3）重复上述过程，最多经过n-1趟扫描后，排序结束
2.代码：
#include
int main()
{
printf("Please input the number of arrays:\n");
int n;
scanf("%d",&n);
printf("Please input the elements:\n");
int a[n];
int i,j,t;
for(i=0;i=a[j+1])
{
t=a[j];
a[j]=a[j+1];
a[j+1]=t;//冒泡排序
}
}
}
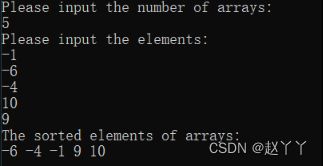
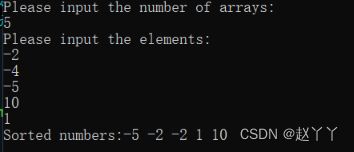
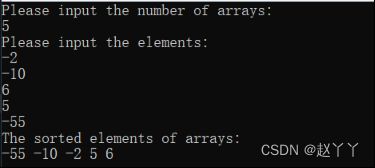
printf("The sorted elements of arrays:\n");
for(i=0;i 3.运行结果：
题目二
题目2：给定n个不同数的数组S和正整数i，i≤n1/2，求S中最大的i个数，并且按照从大到小的次序输出。用至少3种算法来实现，并分析其时间复杂度。
方法一：冒泡排序
1.算法原理：对S 进行冒泡排序，然后输出S 中最大的i 个数。
冒泡排序：主要有两个过程，①两两元素相比较 ，如果升序情况下大的往后排 ，降序情况下小的往后排（本例采用降序）②排序在最右端的代表已经排好序的，将不再参与大小比较
其时间复杂度：TA(n)=(n-1) + (n-2) + (n-3) + …+1=O(n2)
2.伪代码：
输入: n个数的数组S[p..r]
输出：元素按从大到小排序的数组S
1. for(开始的索引K=0; K <数组的长度;K++) {
2. for(剩余未排序的索引J=0; J < 当前未排序的长度; J++) {
3. if(数组[J]<数组[J+1]) {
4. 数组[J] 跟 数组[J+1] 调换位置
5. }
6. }
7.}
3.代码实现
#include
#include
#define SIZE 10 //定义数组大小
//主函数
int main(void) {
void bubble(int a[], int n);
int n = SIZE;
int b[n];
printf("请输入数组:\n");
for (int i = 0; i < n; i++) {
scanf("%d", &b[i]);
}
bubble(b, n);
printf("冒泡排序之后为:\n");
for (int i = 0; i < 10; i++) {
printf("%d ", b[i]);
}
int bound = pow(10,0.5);
printf("\n数组中最大的i个数为:\n");
for (int i = 0; i < bound; i++) {
printf("%d ", b[i]);
}
}
//冒泡排序过程
void bubble(int a[], int n) {
int i, j, temp;
for (i = 1; i < n; i++) {
for (j = 0; j < n - i; j++) {
if (a[j] < a[j + 1]) {
temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
}
4.运行结果展示
由于冒泡排序的时间复杂度较大，对100万级的数据运行很慢，故未使用冒泡排序对100万数据进行运行。
方法二：堆排序
1.算法原理：堆排序分为两个部分：堆调整+堆排序
其思路是：将一个已知的序列先调整到大堆的形式，然后再将堆顶元素和堆最后的元素进行调换（这样最大的元素就在最后面了），减去最后一个元素将剩余的元素进行堆调整，重复上面的步骤就会生成从小到大的序列。（反之即为从大到小的序列）
2.代码：
import pandas as pd
import numpy as np
import math
import copy
import time
#读取文件中的数据
df=open("D:\\courses\\Algorithm\\100万.txt")
list1=[]
for line in df:
list1.append([int(x) for x in line.split(" ")])
#堆排序
time_start=time.time()#开始计时
list1[0].sort(reverse = True )#从大到小排列
print(list1[0])
time_end=time.time() #结束计时
time_c=time_end-time_start
print("堆排序所用时间：",time_c,'s')
#输出排序后的数据
f=open("D:\\courses\\Algorithm\\out1.txt","w")
for row in list1:
print(row ,file=f)
#输出前1000大的数
with open("D:\\courses\\Algorithm\\1\\out1.txt") as f1:
list2=[]
for line in f1:
list2.append(list(line.split(","))[0:999])
#print(list2)
f2=open("D:\\courses\\Algorithm\\1\\堆排序前1000位.txt","w")
for row in list2:
print(row ,file=f2)
3.运行结果展示
算法时间复杂度：首先堆调整，堆调整的时间复杂度为O(n)，堆排序的时间复杂度为O(nlogn)，故假设节点数为n,所以需要进行n - 1次调换，也就是需要n-1次堆调整，每次堆调整的时间复杂度为O(logn) ，那么总的时间复杂度就是
(n - 1)O(logn) = O(nlogn)
所以最后堆排序的时间复杂度为：O(n) + O(nlogn) = O(nlogn）
方法三：分治策略
1.算法原理：
利用分治策略，把前k大的都弄到数组最右边，然后对这最右边k个元素排序后再输出。
输入：一个整数n，表示数组的大小。
n个整数，用来表示数组的元素，整数之间以一个空格分开。
一个小于n的整数k，表示输出前k大元素。
输出：从大到小输出前k大的数
我们引入一个操作arrangeRight(k):把数组（或数组的一部分）前k大的都弄到最右边，具体如何将前k大的都弄到最右边?
第一步：设key=a[0],将key挪到适当位置，使的比key小的元素都在key左边，比key大的元素都在key右边。
第二步：选择数组的前部或后部再进行arrangeRight操作：若后部个数正好等于k时，直接输出；若后部个数大于k，则对后部再进行arrangeRight操作；若后部个数小于k，则对前部再进行arrangeRight操作。
其时间复杂度：TC(n)=O(n+klogk)
将前k大的都弄到最右边时间复杂度为O(n),
对k个元素排序后再输出时间复杂度为O(klogk)。
2.代码设计
import pandas as pd
import numpy as np
import time
def partition(mylist, start, end):
# 若选其他元素作为pivot，下面的while内容需要相应更改
pivot = mylist[end]
left = start
right = end
while left < right:
while left < right and mylist[left] >= pivot:
left += 1
while left < right and mylist[right] <= pivot:
right -= 1
if left != right:
mylist[left], mylist[right] = mylist[right], mylist[left]
mylist[end], mylist[left] = mylist[left], pivot
return left
def quick_sort(mylist, start, end):
"""
mylist: 待排序的 list
start: mylist第一个元素索引
end: mylist最后一个元素索引
"""
if start < end:
mid = partition(mylist, start, end)
quick_sort(mylist, start, mid - 1)
quick_sort(mylist, mid + 1, end)
#读取文件中的数据到列表
df=open("D:\\courses\\Algorithm\\100万.txt")
list1=[]
for line in df:
list1.append([int(x) for x in line.split(" ")])
time_start=time.time()#开始计时
quick_sort(list1[0],0,len(list1[0])-1)
time_end=time.time() #结束计时
time_c=time_end-time_start
print("快速排序所用时间：",time_c,'s')
#输出排序后的数据到文件
f=open("D:\\courses\\Algorithm\\out3.txt","w")
for row in list1:
print(row ,file=f)
#输出前1000大的数
with open("D:\\courses\\Algorithm\\1\\out3.txt") as f1:
list2=[]
for line in f1:
list2.append(list(line.split(","))[0:999])
#print(list2)
f2=open("D:\\courses\\Algorithm\\1\\快速排序前1000位.txt","w")
for row in list2:
print(row ,file=f2)
3)运行结果展示
方法四：二路归并排序
1.算法原理：对S 进行二路归并排序，并输出S 中最大的i 个数。
第一步：首先要将数组进行划分，设待排序的数组是A[SIZE]。我们每次从数组中间开始划分，划分形式如同一棵二叉树。
第二步：划分必定是一个递归的操作。因此设计一个类似于二叉树遍历的递归代码。
函数名为MergeSort( A[] ，int low , int high)，每次对A[low…high]进行划分，划分为A[low…mid]、A[mid+1…high]，然后再对这两段数组进行递归的划分。
划分到单一元素的时候，进行合并操作。
第三步：合并操作。对于任意两个有序的数组，将它们合并。
在合并的时候，比如我们对A[2，4，6，1，3，5]。在中间划分，分成了两个小数组，这时在原址上合并，会造成数据丢失。因此，我们需要一个辅助数组B，和A一模一样，在B的基础上进行判断操作，在A的基础上进行排序操作。
情况1 两个有序数组，刚好全部排序好。
情况2 其中一个数组一个元素都没有了，但是另一个数组里，还有很多元素，这种情况下，这个数组里剩余的元素肯定都是小于已经排序好的那一部分(本例用从大到小)。比如 A[4，2，1] B[6，5，3],当排序到[6，5，4，3]的情况下，B已经没了，但是A还有[2，1]这两个元素，这两个元素肯定是比所有的已排序的小的，直接接到已排序的后面就好。
其时间复杂度：TB(n)=O(n*logn)
因为每次合并，都要遍历一下整个数组，故每次合并，都花费O(n)的时间，
而合并的总次数，是树的高度logn，即一共合并logn次
故时间复杂度 O(nlogn)
2.伪代码
Merge Sort(S,p,r)
输入: n个数的数组S[p..r]
输出：元素按从大到小排序的数组S
1.if p3.代码如下
import pandas as pd
import numpy as np
import time
def merge(mylist, l, m, r):
n1 = m - l + 1
n2 = r - m
# 创建临时数组
L = [0] * (n1)
R = [0] * (n2)
# 拷贝数据到临时数组 arrays L[] 和 R[]
for i in range(0, n1):
L[i] = mylist[l + i]
for j in range(0, n2):
R[j] = mylist[m + 1 + j]
# 归并临时数组到 arr[l..r]
i = 0 # 初始化第一个子数组的索引
j = 0 # 初始化第二个子数组的索引
k = l # 初始归并子数组的索引
while i < n1 and j < n2:
if L[i] <= R[j]:
mylist[k] = L[i]
i += 1
else:
mylist[k] = R[j]
j += 1
k += 1
# 拷贝 L[] 的保留元素
while i < n1:
mylist[k] = L[i]
i += 1
k += 1
# 拷贝 R[] 的保留元素
while j < n2:
mylist[k] = R[j]
j += 1
k += 1
def mergeSort(mylist, l, r):
if l < r:
m = int((l + (r - 1)) / 2)
mergeSort(mylist, l, m)
mergeSort(mylist, m + 1, r)
merge(mylist, l, m, r)
#读取文件中的数据到列表
df=open("D:\\courses\\Algorithm\\100万.txt")
list1=[]
for line in df:
list1.append([int(x) for x in line.split(" ")])
time_start=time.time()#开始计时
mergeSort(list1[0],0,len(list1[0])-1)
time_end=time.time() #结束计时
time_c=time_end-time_start
print("快速排序所用时间：",time_c,'s')
#输出排序后的数据到文件
f=open("D:\\courses\\Algorithm\\out4.txt","w")
for row in list1:
print(row ,file=f)
#输出前1000大的数
with open("D:\\courses\\Algorithm\\1\\out4.txt") as f1:
list2=[]
for line in f1:
list2.append(list(line.split(","))[0:999])
#print(list2)
f2=open("D:\\courses\\Algorithm\\1\\二路归并排序前1000位.txt","w")
for row in list2:
print(row ,file=f2)
4.运行结果展示
题目三
题目3：求两个序列的最长公共子序列。
方法一：穷举法
即对X的每个子序列，检查它是否也是Y的子序列，从而确定它是否为X和Y的公共子序列，并且在检查过程中选出最长的公共子序列。
X的一个子序列相应于下标序列{1, 2, …, m}的一个子序列，因此，X共有2m个不同子序列。同样，Y的一个子序列相应于下标序列{1, 2, …, n}的一个子序列，因此，X共有2n个不同子序列。故穷举搜索法需要指数时间（2m * 2n）。
方法二：动态规划
1.原理
动态规划算法：最优子结构性质
记：Xi={x1,…,xi}，即X序列的前i个字符（
）
Yj={y1,…,yj}，即Y序列的前i个字符（
）
假定
c[i] [j]数组：指只取X前i个元素和只取Y前j个元素能够得到的最长公共子序列的值（即存放最优子结构的值）
（1）若xm=yn（最后一个字符相同），该字符必是X与Y的任一最长公共子序列Z（设长度为k）的最后一个字符，即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1）。
（2）若xm≠yn，则Z∈LCS(Xm-1, Y)或Z∈LCS(X , Yn-1)。若zk≠xm则有Z∈LCS(Xm-1 , Y)，类似的，若zk≠yn 则有Z∈LCS(X , Yn-1)。此时，问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为：max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。
综上，可以得出递推式：
2.伪代码
for x = 0 to n do
for y = 0 to m do
if (x == 0 || y == 0) then
LCS(x, y) = 0
else if (Ax == By) then
LCS(x, y) = LCS(x - 1,y - 1) + 1
else
LCS(x, y) = ) max(LCS(x – 1, y) , LCS(x, y – 1))
endif
endfor
endfor
3.代码
求LCS的长度
using namespace std;
char a[1001], b[1001];
int c[1001][1001], len1, len2;
void lcs(int i, int j)
{
for (i = 1; i <= len1; i++)
{
for (j = 1; j <= len2; j++)
{
if (a[i - 1] == b[j - 1])
c[i][j] = c[i - 1][j - 1] + 1;
else if (c[i - 1][j] > c[i][j - 1])
c[i][j] = c[i - 1][j];
else
c[i][j] = c[i][j - 1];
}
}
}
int main()
{
while (~scanf(" %s", a))
{
scanf(" %s", b);
memset(c, 0, sizeof(c));
len1 = strlen(a);
len2 = strlen(b);
lcs(len1, len2);
printf("%d\n", c[len1][len2]);
}
return 0;
}
运行结果：输入两个序列以空格隔开，abcfbc abfcab，可得出它们的最长公共子序列长度为4，programming contest，LCS的长度为2，abcd mnp，LCS的长度为0。
求LCS的具体序列：
对于一个最优子结构c[i][j]的来源一共有三个，分别是
1）c[i] [j] = c[i - 1] [j - 1] + 1，
2）c[i] [j] = c[i - 1] [j] ；
3）c[i] [j] = c[i] [j - 1]；
为了自底向上计算子问题的最优值，可以创建一个临时的数组b[i][j]用来记录这三个来源，从而根据最值反向追踪最长公共子序列：
1）b[i] [j] = 1, 即表示取了x[i]或y[j]作为最长公共子序列的一部分，输出即可。
2）b[i] [j] = 2，即表示当前c[i] [j]的状态来自c[i - 1] [j],这时需要追踪c[i - 1] [j]。
3）b[i] [j] = 3， 即表示当前c[i] [j]的状态来自c[i] [j - 1],这时追踪c[i] [j - 1]。
这种方法按照反序来找LCS的每一个元素的。由于每个数组单元的计算耗费O(1)时间，所以构建c[i][j]表的算法时间复杂度O(nm),空间复杂度也是O(nm)，输出1个LCS的序列需要O(m+n)。
const int N = 1010;
char s1[N], s2[N];
int len1, len2;
int c[N][N];
int b[N][N];
void print(int i, int j){
if(i == 0 || j == 0)return;
if(b[i][j] == 1){
print(i - 1, j - 1);
cout<>len1>>len2;
//输入需要求最长公共子序列的序列s1和s2
cin>>s1+1>>s2+1;
for(int i = 1; i <= len1; i ++){
for(int j = 1; j <= len2; j ++){
if(s1[i] == s2[j]){
c[i][j] = c[i - 1][j - 1] + 1;
b[i][j] = 1;
}
else if(c[i - 1][j] >= c[i][j - 1]){
c[i][j] = c[i - 1][j];
b[i][j] = 2;
}
else {
c[i][j] = c[i][j - 1];
b[i][j] = 3;
}
}
}
print(len1, len2);
// cout< 
运行结果：输入X序列的个数7、Y序列的个数6，Xi={A,B,C,B,D,A,B},Yi={B,D,C,A,B,A}，输出X,Y序列的最长公共子序列{B,C,B,A}。
为了节省空间，也可以不使用临时数组b,直接通过c数组判断即可。
const int N = 1010;
char s1[N], s2[N];
int len1, len2;
int c[N][N];
void print(int i, int j) {
if (i == 0 || j == 0)return;
if (c[i][j] == c[i - 1][j - 1] + 1) {
print(i - 1, j - 1);
cout << s1[i];
}
else if (c[i][j] == c[i - 1][j])print(i - 1, j);
else print(i, j - 1);
}
int main()
{
//最优子结构状态值初始化
memset(c, 0, sizeof(c));
//输入序列s1和s2的长度
cin >> len1 >> len2;
//输入需要求最长公共子序列的序列s1和s2
cin >> s1 + 1 >> s2 + 1;
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (s1[i] == s2[j])c[i][j] = c[i - 1][j - 1] + 1;
else c[i][j] = max(c[i - 1][j], c[i][j - 1]);
}
}
cout<
运行结果：输入X序列的个数7、Y序列的个数8，再输入Xi={a,b,c,i,c,b,a},Yi={a,b,d,k,s,c,a,b}
输出X,Y序列的最长公共子序列个数4，序列为{a,b,c,a}。
4.图解过程
以字符串s1=“ABCBDAB”,S2=“BACDBA”为例。
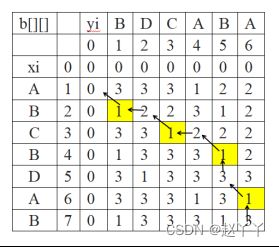
（1）初始化len1=7，len2=6，初始化c[][]第一行、第一列元素为0。
（2）i=1:s1[0]与s2[j-1]比较，j=1,2,3…len2。即“A”与“BDCABA”分别比较一次。
如果字符相等，c[i][j]取左上角数值加1，记录最优值来源b[i][j]=1。
如果字符不等，取左侧和上面数值中的最大值，如果左侧和上面的数值相等，默认取上面数值，如果c[i][j]的来源于左侧b[i][j]=2，来源于上面b[i][j]=3。
（3）继续处理i=2,3,…,len1:s1[i-1]与s2[j-1]比较，j=1,2,3,…,len2。
（4）c[][]右下角的值即为最长公共子序列的长度。c[7][6]=4，即字符串s1=“ABCBDAB”,S2=“BACDBA”的最长公共子序列的长度为4。
（5）构造最优解，首先读取b[7][6]=3,说明来源为3，向左找b[6][6]，继续查找，当b[i][j]=1,找左上角，返回时输出字符，b[i][j]=0,找上面。b[1][0]中列为0，算法停止，返回输出最长公共子序列BCBA。
方法三：闫氏DP分析法
状态表示（化零为整）：f[i][j]每一个条件对应一个维度。总集合表示的是所有序列A[1 ~ i]和序列B[1 ~ j]的公共子序列的集合。集合的属性是最大值。
状态计算（化整为零）：找到最后一步的不同点，即为A[i]是不是包含在子序列里，B[j]是不是包含在子序列里。若1为包含，0为不包含，则应该有四个不同的选择，即（00，01，10，11）。
（1）00即A[i]和B[j]都不包含在公共子序列里，最大值就为f[i-1][j-1]。
（2）01即不包含A[i]但是包含B[j]，如果将其表示成f[i-1][j],实际上有两种可能：
a.不包含A[i]但是包含B[j]
b.不包含A[i]也不包含B[j]
可以发现在分析第二类状态时覆盖了第一类状态，所以不需要单独计算第一类状态，只计算第二类状态，就可以得出第一类状态的最大值和第二类状态的最大值的max。
（3）10即包含A[i]，不包含B[j]，与第二类状态同理，为f[i][j-1]。
（4）11即A[i]和B[j]都包含在公共子序列里，这个子集存在时有一个前提条件，就是A[i]=B[j]，A[i]之前的A和B[j]之前的B可以随便选（变化部分），但是最后一定要A[i]和B[j]都选（不变部分），所以要留下一个长度1。所以这个状态的最大值就是f[i-1][j-1]+1。
综上所述，我们只需考虑01,10,11这三种情况即可。
const int N = 1010;
char a[N], b[N];
int n, m;
int f[N][N];
void print(int i, int j) {
if (i == 0 || j == 0)return;
if (f[i][j] == f[i - 1][j - 1] + 1) {
print(i - 1, j - 1);
cout << a[i];
}
else if (f[i][j] == f[i - 1][j])print(i - 1, j);
else print(i, j - 1);
}
int main() {
cin >> n >> m >> a + 1 >> b + 1; //这里+1的意思是使下标从1开始。
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
f[i][j] = max(f[i - 1][j], f[i][j - 1]); //先找到第二集合的最大值与第三集合的最大值的max
//因为第二集合包含了第一个一集合，所以不用单独计算第一个集合。
if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1); //再将一二三集合比出的最大值与第四集合的最大值比较取max。
}
}
cout << f[n][m] << endl;
print(n, m);
return 0;
}
运行结果：输入X序列的个数7、Y序列的个数6，Xi={A,B,C,A,D,A,B},Yi={B,A,C,D,B,A}
输出X,Y序列的最长公共子序列个数4，序列为{A,C,D,B}。
题目四
题目4：最大子段和问题，用至少三种方法求解，并比较它们的复杂度。
方法一：蛮力法
1.原理
在该方法中，用两个for循环求出最大子段和的值，并返回该值，由于用了两个for循环遍历，所以可以得出用暴力求解法得出的时间复杂度为
。
2.代码
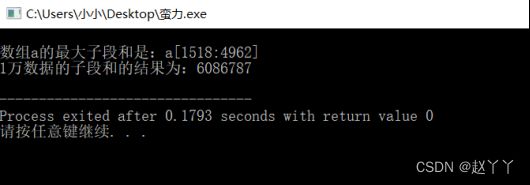
（1）蛮力法求解—常规数据：
#include
#include
#include
using namespace std;
//该算法的时间复杂度是O（n*n）
//蛮力法
int maxSum(int n, vector a, int &starti, int &endj) {
int sum = a[0];
for(int i = 0; i < n; i++) {
int thisSum = 0;
for(int j = i; j < n; j++) {
thisSum += a[j];
if(thisSum >= sum) {
sum = thisSum;
starti = i;
endj = j;
}
}
}
return sum;
}
int main() {
vector a;
int t,sum;
cout<<"请输入数组元素的值："<>t) {
a.push_back(t);
if(cin.get()=='\n') //遇到回车退出
break;
}
int length = a.size();
int starti,endj;
cout< （2）蛮力法求解—1万数据：
#include
#include
#include
using namespace std;
//该算法的时间复杂度是O（n*n）
//蛮力法
int maxSum(int n, int a[], int &starti, int &endj) {
int sum = a[0];
for(int i = 0; i < n; i++) {
int thisSum = 0;
for(int j = i; j < n; j++) {
thisSum += a[j];
if(thisSum >= sum) {
sum = thisSum;
starti = i;
endj = j;
}
}
}
return sum;
}
int main() {
int a[10000];
int starti, endj,sum;
FILE* fp;
fp = fopen("C:/Users/小小/Desktop/1万.txt","r");
for(int i=0;i<10000;i++){
fscanf(fp,"%d",&a[i]);
}
cout< 3.测试结果
方法二：分治法
1.分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。即一种分目标完成程序算法，简单问题可用二分法完成。
在该题中，采用分治算法，假设数组为
，该数组有n个元素，下标从0开始，初始位置为left，结束位置为right，则中间位置为
。可以分析得出
的最大子段和有三种情形：
（1）
的最大子段和与
的最大子段和相同；
（2）
的最大子段和与
的最大子段和相同；
（3）
的最大子段和为
，且
。
其中，（1）和（2）两种情形可以由递归求得。
对于情形（3），
和
在最优子序列中，
的最大子段是
的最大子段和与
最大子段和的和。
分治算法的时间复杂度为：
从而可以得
。
2.代码
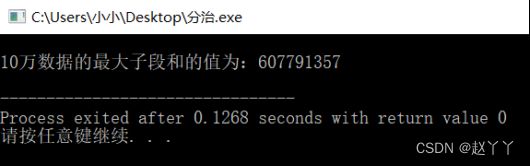
分治法求解—10万数据：
#include
#include
using namespace std;
int MaxSubArray(int a[],int left,int right) {
int mid=(left+right)/2;
int s1,s2,sum=0;
int starti,endj;
int max=-10000; //max相当于s3 左右相加
if(left==right) {
return a[left];
}
s1=MaxSubArray(a,left,mid); //左递归
s2=MaxSubArray(a,mid+1,right); //右递归
endj=mid;
for(int i=mid; i>=left; i--) { //从左半部分最后一个数向前加找出最大值
sum+=a[i];
if(max 3.测试结果
方法三：动态规划法
1.原理
第三种方法采用动态规划求解，这里我们求解该题的算法思路是： 首先设置一个状态
，该状态表示以第i个元素结尾的子序列的最大值。令
、，其为动态规划的初始条件。然后设状态转移方程为
，
取两者中的最大值，该方程也可以理解为当
为负数时，
的取值为
，若
为正时，
的取值为
。然后设一个变量SumMax，其初值设为
，然后令
，即不断更新SumMax的值，SumMax最终的值即为最大字段和的值。由设计出的算法可知，利用动态规划求解的时间复杂度为
。
综上可以得出，动态规划算法的时间复杂度最低，所以利用动态规划算法求解最大子段和问题的效率最高。
2.算法实现
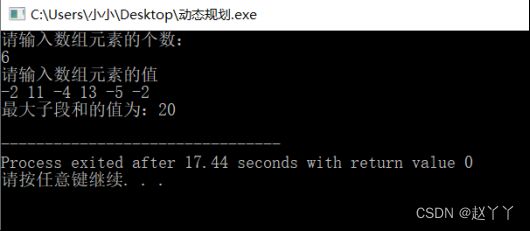
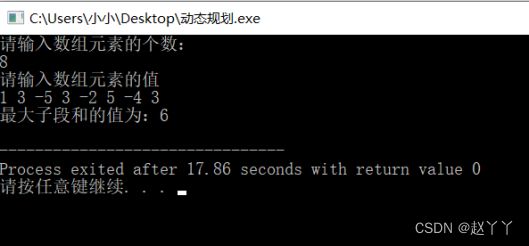
（4）动态规划算法求解—100万数据：
#include
#include
using namespace std;
int a[1000000];
int f[1000000]={-0x3f3f3f3f};
int main(){
FILE* fp;
fp = fopen("C:/Users/小小/Desktop/100万.txt","r");
for(int i=0;i<1000000;i++){
fscanf(fp,"%d",&a[i]);
}
f[0]=a[0];
int SumMax=f[0];
for(int i=1;i<1000000;i++){
// cin>>a[i]; //输入数组元素的值
f[i]=max(f[i-1]+a[i],a[i]);//(1<=i<=n-1)
SumMax=max(f[i],SumMax);
}
cout<<"100万数据的最大子段和的值为："< 3.测试结果
四、 设计技巧及体会
1、对设计进行评价，指出合理和不足之处，提出改进的方案。
本次课内实验算法设计基本满足老师的要求，但因为是第一次实验课，算法设计过程和代码编写过程比较艰辛。
本次实验课中表现比较好的地方是：通过大家共同探讨努力，四道题都按时完成并且使用了至少三种方式来进行实现，算法的时间复杂度和空间复杂度都满足要求，但不足之处也同样存在，包括程序编写完成后在面对100万的数据测试集时程序的运行或多或少都需要一些修改，尽管在改进之后完成了展示，但是还是可以看出大家在程序编写与算法设计的过程中还有考虑不周到的地方，在后续的课内实验算法设计与代码编程过程中还需要多考虑这种大数据量的测试集对于程序运行的影响。
2、在设计过程中的感受。
（1）本次实验过程中主要是对快速排序、二路归并排序、冒泡排序等排序算法的思想和动态规划有了更深层次的理解与体会，用C/C++/python实现的代码也更加熟悉，在实验过程中更加理解了算法的思想。
（2）针对每个问题，实现的算法有好多种，具体使用哪种要根据对其时间复杂度和空间复杂度的分析比较进行，我们在以后的编码过程中要尽量编写简单高效的代码，尽量争取所用的时间复杂度小一点。
（3）本次实验对100万数据集的排序对算法要求更加严格，更要求算法效率。
（4）此次小组合作实验让我们受益匪浅，不仅让我们注意搜集资料、组织好小组成员共同分工，也让我们体会到动手实践、自主探索与合作交流是学习的重要方式之一。在后面的实验课程中应该更注重小组成员之间的相互讨论，共同学习共同进步。