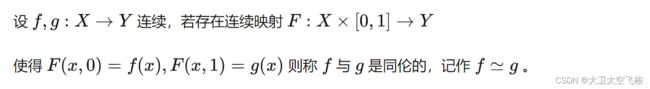计算共形几何-代数拓扑
摘自团队文章,计算共形几何 - 知乎。
计算共形几何是丘成桐先生和顾险峰教授共同创立的跨领域学科,完美的融合现代几何拓扑理论与计算机科学,将代数拓扑、微分拓扑、曲面微分几何、黎曼面理论、最优传输理论的基本概念、关键定理和思想方法推广到离散情形,转换成计算机算法。
共形几何植根于基础数学,是很多领域的交叉点:黎曼面理论、复分析、微分几何、代数拓扑、几何偏微分方程、代数曲线等等;计算共形几何和计算机科学中的计算几何、数字几何和数值偏微分方程也有亲缘关系。这门学科的诞生是因为三维技术的蓬勃兴起,特别是三维扫描技术(例如基于结构光的相位平移技术)、计算机图形学技术(例如曲面参数化、纹理贴图技术)、计算机视觉技术(例如曲面注册配准,人脸表情捕捉)的迅猛发展,使得传统的欧几里得几何和线性代数方法无法解决这些领域提出的深刻问题,工程医疗领域必须系统引入现代微分几何和拓扑的思想和方法,发展严密而实用的计算方法。计算共形几何响应了时代的呼唤,从第一性原理出发推动了科学技术的发展。
共形几何主要应用包括计算机图形学中的全局曲面共形参数化、保面积参数化、计算机视觉中的动态曲面配准以及3D视觉领域的应用,例如立体视觉、点云融合、曲面重建、网格生成、几何压缩等等。2022年的科技热点在于自动驾驶、工业软件、可解释人工智能和元宇宙等领域,共形几何的理论和算法有助于直接解决这些领域的一些基本问题。共形映射指将一张曲面映射成另外一张曲面,保持角度不变,同时保持局部形状不变。
上图米开朗基罗的大卫王雕像被共形地映到平面长方形,这个映射的特性有:
- 曲率发生巨大变化,把弯曲的曲面变成了平直的平面。
- 虽然局部面积发生变化,但局部形状保持不变,比如眼睛、耳朵、发髻。
局部面元的变化率和曲面的平均曲率完整地保持了原来曲面所有的几何信息,我们可以用面元变化率和平均曲率来完全重建原始曲面。
现实世界中所有可能的形状,在共形变换下最终会变成三种标准曲面中的一种:球面、欧式或双曲空间。大千世界,各种形状千变万化,纷繁复杂,有无穷多种可能。基于计算共形几何的单值化定理,极大地简化了理论探讨和算法设计。
工程中碰到的几何畸变可以分成两类:局部形状的畸变和局部面积元的畸变。如果使得局部形状被保持,即映射局部是相似变换,但是相似比逐点不同,所得的映射是共形映射(conformal mapping),由共形几何理论来研究;如果使得面积元被保持,则所得映射为最优传输映射,由最优传输理论来刻画。在很多环节,计算共形几何提供了解决这些问题的唯一的可行方法。
下面介绍计算共形几何涉及的代数拓扑/微分拓扑、算法和工程应用等核心内容。
视频链接:顾险峰清华大学计算共形几何2018_哔哩哔哩_bilibili
本文按照理论、算法设计和应用的逻辑来写,主要介绍代数拓扑和微分拓扑,依此介绍了同伦理论、同调理论、覆盖空间理论、Brouwer 不动点理论,特别是微分流形上的微积分,以微分形式和外微分来推广场论,矢量场奇异点的 Poincare-Hopf 指标定理,微分拓扑中的 de Rham 上同调理论和 Hodge 分解理论。主要解决工程中三大问题:曲面配准、几何分类和几何分析,使用的核心研究工具是计算共形几何。
- 曲面配准:把一张脸变成另一张脸,动画中叫表情迁移,需要两个曲面的微分同胚。
- 曲面分类:比如表情识别,判断三维的人脸是什么表情,是哭或者笑?
- 几何分析:得到人体的器官表面,判断其是否有肿瘤;通过分析大脑皮层的曲面,判断是否有脑疾病?
几何是研究各种变换群下的不变量,工程上常用的几何是:
- 黎曼几何:等距变换,这里的距是指测地距离。把一张长方形纸卷成圆柱,上面任意两点之间的最短距离不变。
- 曲面微分几何:高斯曲率不变和主曲率不变,一个曲面嵌入到三维空间中,那么它可以在三维空间中进行旋转和平移。
- 拓扑Topology:几何图形或空间在连续改变形状后还能保持不变的一些性质,它只考虑物体间的位置关系而不考虑它们的形状和大小。在拓扑学里不讨论两个图形全等的概念,但是讨论拓扑等价的概念。比如,圆和方形、三角形的形状、大小不同,但在拓扑变换下,它们都是等价图形;足球和橄榄球,也是等价的——从拓扑学的角度看,它们的拓扑结构是完全一样的。而游泳圈的表面和足球的表面则有不同的拓扑性质,比如游泳圈中间有个“洞”。在拓扑学中,足球所代表的空间叫做球面,游泳圈所代表的空间叫环面,球面和环面是“不同”的空间。
顾老师研究的计算共形几何介于拓扑和黎曼几何之间,由于经常需要对曲面进行大形变,比如把弯的曲面变成直的平面,此时曲率将不再被保持,所以黎曼几何不太适用。
拓扑变换太剧烈,保留的信息太少,即太"软",黎曼几何太"硬",没办法把弯曲的变成平的曲面。计算共形几何软硬适中,特别适合研究大的形变。
共形变换和一般微分同胚的本质差别
上图比较了共形变换和拟共形变换。我们将人脸曲面映射到平面圆盘,在平面圆盘上放置很多彼此相切的小圆,构成圆盘填充 (circle packing) 的模式,平面小圆被映射拉回到曲面上。上面一行显示的是共形映射,平面上的无穷小圆被映射拉回到曲面上的无穷小圆;下面一行显示的是一般的微分同胚,这里是拟共形映射,平面上的无穷小圆被映射拉回到曲面上的无穷小椭圆,由此可见,共形映射保持无穷小圆。
(作者注:把同一张三维人脸映射到单位圆盘上,上面一行共形变换是圆到圆,圆的大小发生变化,但是形状没有改变,这个变换称为黎曼映照。可以证明,从人脸到圆盘所有的共形变换彼此之间相差一个三维的群,也就是说有无穷多个变换,但这无穷多个变换可以用三个参数来刻画,因此维数有限。下面一般微分同胚是椭圆到圆,微分同胚有无穷多个,构成的空间也是无穷多维。这是共形变换和拟共形变换最大的差别,共形变换三个参数就可以控制,而且有唯一性,这为工程计算带来很多好处。)
计算共形几何中几个最基本问题
- 给定曲面黎曼度量,如何计算该共形结构。
- 给定曲面高斯曲率,能否设计出一个黎曼度量。
- 给定两个曲面,如何计算两个曲面的拟共形变换。
- 给定两个拓扑等价曲面,他们之间不见得存在保角变换,如何计算不变量来判断两个曲面是否存在保角变换。
- 计算中通常需要找到简单的度量或者曲率来简化计算,如何在共形结构中找到最简单的黎曼度量。
- 两个拓扑等价但是不存在保角变换的曲面,能否找到一个映射,使他最接近保角变换,使得局部形状畸变达到全局最小。这些变换是否存在;是否唯一;计算起来是否稳定。
共形几何计算方法
共形结构的研究方法包括复分析(平面区域的保角变换),代数拓扑和微分几何。因为具有共形结构的曲面是黎曼面,我们采用微分几何的途径,通过黎曼度量来研究共形结构。度量曲面上共形结构的计算方法分为调和映照,全纯微分和 Ricci flow 三大类。
下面开始介绍代数拓扑核心内容
代数拓扑主要目的是把拓扑范畴的问题换成代数问题,包括拓扑空间、结构不变性的映射、同伦群与同调群等。
函子性质(Functor)是描述拓扑空间有代数结构不变量的重要语言。一般地,两个拓扑空间有连续映射,那么可以诱导出它们在对应点的基本群同态,并且若这两个拓扑空间同胚,那么它们对应点的基本群同构。
上图偏下内容介绍了构成群的四个特点(封接幺逆),现实中整数在加法上成群,所有有理数在乘法上成群,魔方所有的操作成群,以及词群等。下面以词群为例介绍群的构成。
群通常表示成Generators和Relators,对这两部分加以比较,可以判断两个群是否同构。
(作者注:从抽象代数的概念上来说,同态和同构是在映射的前提下谈的。
(作者注:拓扑同胚:在拓扑学中,同胚 (homeomorphism、topological isomorphism、bi continuous function) 是两个拓扑空间之间的双连续映射。同胚是拓扑空间范畴中的同构。)
代数拓扑由庞加莱创立。基本群的想法比较直观:假如我们是生活在曲面上的蚂蚁,一辈子没有跳离过曲面,因此没有三维的概念。那么,我们如何判断我们生活的曲面是否有“洞”?
如果蚂蚁比较智慧,它会追踪曲面上的封闭路径。拓扑球面上,所有的圈都能够缩成一个点;拓扑轮胎上,存在一些圈无法缩成点。“圈是否能够缩成点”的思想成为了同伦伦的源头。
代数拓扑由庞加莱创立。基本群的想法比较直观:假如我们是生活在曲面上的蚂蚁,一辈子没有跳离过曲面,因此没有三维的概念。那么,我们如何判断我们生活的曲面是否有“洞”?
如果蚂蚁比较智慧,它会追踪曲面上的封闭路径。拓扑球面上,所有的圈都能够缩成一个点;拓扑轮胎上,存在一些圈无法缩成点。“圈是否能够缩成点”的思想成为了同伦伦的源头。
定义path、loop、product,完成群的构造。
定义同伦homotopy,譬如我们考察曲面上的道路,如果两条道路具有相同的起点和终点,并且条道路能够在曲面上渐变成另外一条道路,则我们说它们彼此同伦。其用处特别广,譬如在解一个复杂的偏微分方程时,先同伦变换成一个简单的方程求解,然后再把方程和解同伦变换回去。严格定义如上公式,
同伦类的核心观点:圈是否可以缩成点。
定义同伦等价homotopy equivalence,如上数学语言。我们考察曲面上过固定点的所有封闭环路(圈)。如果不脱离曲面,一个圈可以逐渐形变成另外一个圈,则这两个圈彼此同伦等价。两个圈可以次第连接,形成一个大圈,如此我们定义圈和圈之间的乘法。{圈的同伦类,乘法}构成了所谓的曲面同伦群。
基本群Fundamental Group或一维同伦群
给定拓扑空间 S 固定基点 p,所有过基点的环路集合为 Γ 所有环路的同伦类集合为 Γ /~,定义乘法,单位元和,逆元定义,那么 Γ /~成群,记为空间的基本群 �1(�,�) 。基本群是代数拓扑最基本的概念,是重要的拓扑不变量,也是共形几何必须掌握的知识。这个概念最早是由庞加莱在19世纪末20世纪初提出并加以研究。(作者注:基本群是从单位闭区间到拓扑空间的闭路的同伦等价类和其运算得到的,是对一个拓扑空间联系一个群的代数结构。)
定义基本群的结构:generators,relators。
解释拓扑等价:是一个非常近现代的概念,直观而言,我们可以想象一个由橡皮膜做成的曲面,通过拉伸收缩,扭曲缠绕,能够形变到另外一个曲面,并且形变过程中,曲面不撕裂、不粘连,则我们说这两个曲面拓扑等价。
(作者注:同伦Homotopy 的概念在拓扑上描述了两个对象间的“连续变化”。 两个拓扑空间如果可以通过一系列连续的形变从一个变到另一个,那么就称这两个拓扑空间同伦;同调,两个流形本身没有边界,其中一个是更高维流形的边界,则两个流形同调。)
拓扑空间之间的拓扑映射诱导了群之间的同态,群同态的行为特征反映了拓扑映射的特质。这一手法被抽象为艰涩的范畴论语言,装神弄鬼,故弄玄虚。拓扑空间和拓扑映射组成了所谓的拓扑范畴{拓扑空间,拓扑映射},群和同态组成了代数范畴{群,群同态}。代数拓扑的手法定义了从拓扑范畴到代数范畴的一个态射,此态射将拓扑空间映成了群,把拓扑映射变成了群同态。至为重要的是,这个态射是“函子”的,这意味着这种范畴间的转化是“保结构的”,信息被尽量保留。这一态射的意义在于将“玄而又玄”的拓扑,变成了朴实无华的计算。
庞加莱猜想 ( Poincaré conjecture ) 内容为:任何一个单连通的,闭的三维流形一定同胚于一个三维的球面。其也称为克雷数学研究所悬赏的七个千禧年大奖难题。
1961年的夏天,在基辅的非线性振动会议上,斯梅尔公布了自己对庞加莱猜想的五维空间和五维以上的证明,立时引起轰动。 斯梅尔由此获得1966年菲尔兹奖。
1983年,美国数学家福里德曼 ( Freedman)将证明又向前推动了一步。在唐纳森工作的基础上,他证出了四维空间中的庞加莱猜想,并因此获得菲尔茨奖。但是,再向前推进的工作,停滞了。
拓扑学的方法研究三维庞加莱猜想没有进展,有人开始想到了其他的工具。瑟斯顿(Thruston)就是其中之一。他引入了几何结构的方法对三维流形进行切割,并因此获得了1983年的菲尔茨奖。
Ricci流是以意大利数学家里奇(Gregorio Ricci)命名的一个方程,用它可以完成一系列的拓扑手术,构造几何结构,把不规则的流形变成规则的流形,从而解决三维的庞加莱猜想。在使用Ricci流进行空间变换时,到后来总会出现无法控制走向的点。这些点叫做奇点。如何掌握它们的动向,是证明三维庞加莱猜想的关键。在借鉴了丘成桐和李伟光在非线性微分方程上的工作后,1993年,汉密尔顿发表了一篇关于理解奇点的重要论文。
在汉密尔顿工作的基础上,三维的情形被俄罗斯数学家格里戈里·佩雷尔曼于2003年左右证明。2006年,数学界最终确认佩雷尔曼的证明解决了庞加莱猜想。庞加莱猜想是一个拓扑学中带有基本意义的命题,将有助于人类更好地研究三维空间,其带来的结果将会加深人们对流形性质的认识。
拓扑球面Topological Sphere上面所有圈可否缩成一个点?该问题是庞加莱猜想的逆问题。
证明:亏格为 1 的情形,包括1,2,3步骤。
证明:亏格为 2、3 的情形。
理解曲面拓扑,重点要会画上面的图,特别是亏格为 2 和 3 的图,画图时注意方向不要搞错。
以上是各种维度曲面的基本群及其推广,下面介绍如何计算。
一类特殊拓扑空间的基本群计算: VAN-Kampen 定理。
借用 VAN-Kampan定理,用数学归纳法来证明N维情形。
介绍另外一种例子:六面体划分,Hexahedral Mesh 网格化是此领域的圣杯问题。
对于给定的三维空间中的区域,具有复杂拓扑和几何,如何自动生成高质量的结构化的六面体网格? 六面体网格是有限元分析中最理想的网格,科学家和工程师一直在为此找寻最理想的方案,但至今没有完美解决,对于复杂的几何,我们仍然需要借助四面体单元,但对于数学家来说,寻找完美的解决方案是情怀和动力所在。这个问题被成为神圣网格问题HOLY GRAIL GRID,可见其重要性。
关于非结构性的六面体网格的存在性理论,早在1980年代由菲尔兹奖得主瑟斯顿(Thurston)洞察到,其主要工具是微分拓扑,特别是光滑同伦理论,其主要的光滑同伦定理由另一位菲尔兹奖得主斯梅尔(Smale)证明。历经几十年的发展,理论上没有实质性改变,近期又由计算拓扑学家(Jeff Erickson)用代数拓扑的语言加以厘清。
结构性的六面体网格的存在性理论,最近被大连理工大学的罗钟铉,雷娜团队和作者合作共同创立,其理论根基是流形的叶状结构理论和黎曼面的亚纯微分理论。这一理论给出了复杂拓扑三维流形六面体网格的存在性证明,并给出了神圣网格的自动生成算法。美国三院院士(国家科学院,国家工程院,国家科学和艺术院),Thomas Hughes教授对于这项工作给与高度评价,他认为这项工作极其重要(Extremely Important)。相对于微分拓扑,叶状结构理论对于问题的刻画更为精致而深刻。
下面引出休斯顿定理:
大名鼎鼎的休斯顿 Thurston 定理、Whisker Alogrithm 算法,在六面体生成领域统领多年,背后依据的理论是光滑同伦理论。(PS:感叹人生应该像Whisker一样,善于寻找成名或者说为世界作出贡献的机会)
证明休斯顿理论,引出光滑同伦理论,进而引出smale定理。smale定理证明(略)。
光滑曲线:处处一阶可导的曲线。
介绍正则同伦或光滑同伦
介绍曲面基本群的典范表示。
介绍图的基本群计算方法,如上图。
Graph cuts 即 Cut Graph 另外一种说法:是一种十分有用和流行的能量优化算法,在图像处理领域普遍应用于前后背景分割(Image segmentation)、立体视觉(stereo vision)、抠图(Image matting)等,目前在医学图像领域应用较多。
此类方法把图像分割问题与图的最小割(min cut)问题相关联。首先用一个无向图,G=
第一种顶点和边是:第一种普通顶点对应于图像中的每个像素。每两个邻域顶点(对应于图像中每两个邻域像素)的连接就是一条边。这种边也叫 n-links。
第二种顶点和边是:除图像像素外,还有另外两个终端顶点,叫 S(source:源点,取源头之意)和 T(sink:汇点,取汇聚之意)。每个普通顶点和这2个终端顶点之间都有连接,组成第二种边。这种边也叫 t-links。
继续介绍算法实现。(笔误:encounter)
根据事实 1,2,诱导出两个群之间同态;(两个流形通过两个群表示出来,方便计算)
根据事实 3,推出同伦等价判断方法。
应用介绍
- 布劳威尔不动点定理
求解方程一直是数学发展的一个源动力,通常求解方程等价于求算子的不动点。如果算子的作用域的拓扑比较复杂,并且算子有扰动,不动点的行为分析就非常有挑战性。关于不动点有三个层次的问题,深刻程度有所差异,所使用的工具也截然不同。第一个层次是不动点的存在性问题,其解答是莱夫希茨(Lefschetz)理论,所用工具是同调论;第二个层次是不动点几何个数的下界,其答案是尼尔森(Nielsen)理论,所用工具是同伦论;第三个层次是下界是否可以达到,所用工具已经超出代数拓扑,而是瑟斯顿的曲面自映射分类理论,属于几何拓扑,与微分几何和共形几何紧密相连。
目前有关计算尼尔森数乃至曲面自映射的不动点的算法程序还没有出现。如何表示复杂拓扑曲面间的映射,如何为曲面配上合适的黎曼度量,如何在映射同伦类中找到合适的代表,如何计算不动点的指标,这些都对目前的计算数学提出了强有力的挑战。但是另一方面,目前似乎还没有为这套理论找到合适的应用。我们相信,不久的将来,依随科技的发展,复杂流形的不动点计算必然会成为关键技术,在工程和医疗领域大显身手。
- 解释 RNN 深度学习、常微分方程 ODE、不动点理论三者之间的关系。
深度学习实质上是在求解微分方程,最终归结在寻找不动点上。
- 简介江泽涵先生在不动点类理论的贡献,后面还有介绍不动点类理论的章节。
开始介绍覆盖空间,严格数学定义如上所示。理解完基本群,算是跨过了第一道门槛,接着需要理解“万有覆盖空间”。覆盖空间是单联通的,所有圈都能缩成点,那么该覆盖空间称为万有覆盖空间。
其严格数学定义:
举例如下:
给定 一个拓扑空间,计算其基本群,通过基本群找到所有的正规子群,每个正规子群代表一类覆盖空间。
原来群除掉正规子群得到商群,那商群有什么作用?
所有拓扑空间一定存在一个万有覆盖空间。 Γ 是一套路径的集合,起点是p点。 Γ 模掉同伦 ∼ ,得到所有道路同伦等价类,道路同伦等价类构成的集合就是万有覆盖空间。
介绍如何构造一个交换群(即模掉中心交换子),并留下作业:如何构造覆盖空间?
介绍同伦检测方法,主要idea是运用lifting。
介绍计算万有覆盖空间的算法,好理解,但计算比较耗资源。
应用:物联网安全路由设计及实现
在物联网中,许多传感器构成网络,我们需要设计路由算法以确保网络传输的安全。如图所示,传感器网络覆盖了平面区域,空心部分是网络无法覆盖的地方,例如池塘。我们希望从点 p 传输消息到达点 q,这里有多条路径可以选择 。
为了增加信息传递的安全性,我们将消息切割成多个包 package,每个包沿着不同的路径进行传递,同时我们要求任意一条路径不能在网络中渐变成另外一条。这意味着不同的路径应该彼此不同伦。因此如何判断两条路径是否同伦,如何设计彼此不同伦的路径,这些都是网络路由安全设计的重要问题,其计算依赖于同伦群的理论。
介绍一种几何拓扑方法计算万有覆盖空间,该算法需要理解的概念比较多,如双曲度量、测地线、Ricci flow等,然更优秀。
下面开始介绍同调论
同调和同伦理论简介:
同伦群,理解同伦群的诀窍是考察圈是否能够缩成一个点。
如果所有的圈都能缩成点,则曲面必为球面。这一结论在三维流形上的推广,就是鼎鼎大名的庞加莱猜测。这一结论的严格数学阐发,就是同伦论。我们考察曲面上过固定点的所有封闭环路(圈),如果不脱离曲面,一个圈可以逐渐形变成另外一个圈,则这两个圈彼此同伦等价。两个圈可以次第连接,形成一个大圈,如此我们定义圈和圈之间的乘法。{圈的同伦类,乘法}构成了所谓的曲面同伦群。同伦群的概念平易近人,言简意赅,它的结构却异常丰富,全面反映曲面拓扑。如果同伦群平庸(即只有单位元),则曲面必为球面。如果同伦群可交换,则曲面必为轮胎。如果同伦群存在有限阶的子群,则曲面必不可定向。同伦群的生成元的个数等于曲面亏格的二倍。
同伦群的每一个正规子群都对应着一个覆盖空间,其商群对应着覆盖空间的覆盖变换群。但是,同伦群不可交换,难以计算。
单纯同调群,理解下同调群的诀窍是考察圈和边的差别。
曲面上的任意一个区域的边界必然是封闭曲线(圈),但是曲面上任意一个圈未必是某个区域的边缘(边),两者的差别就是同调。如果曲面上所有的圈都是边,那么曲面必然是球面。这一观点的严密代数化,就是同调群。两个圈如果相差一个边缘,则它们是互为同调的。所有同调类在加法的意义下成群。同调群是同伦群的简化版,同调群都是可交换群,因此理论上同调运算可以完全由线性代数所胜任。所谓单纯就是简单,这里是指所有的概念都是定义在曲面的三角剖分之上的:曲面区域表示成有向面的并集,封闭曲线表示成有向边的队列,边缘算子表示成线性矩阵。同调群的计算最终归结为代数矩阵运算。
上同调群,理解上同调群的诀窍是考察无旋场和梯度场的差别。
德-拉姆de Rham上同调群是定义在微分形式上的。如果曲面具有黎曼度量,我们可以将微分形式等价地理解为切矢量场。取曲面上任意函数,其梯度场的旋量必处处为零。但是,曲面上任意一个无旋场未必是梯度场。无旋场和梯度场之间的差别就是上同调。两个无旋场如果相差一个梯度场,则它们是互为上同调的。所有上同调类在加法的意义下成群。我们可以沿着封闭曲线在矢量场里积分,因此上,下同调群互为对偶。
PS:上同调与调和场内容,后面章节有详细介绍。
调和微分上同调群,调和矢量场是曲面上旋度为零,散度为零的矢量场。所有调和场在加法意义下成群,被称为是曲面的调和微分群。
每一个上同调类中存在一个唯一的调和场,因此调和微分上同调群和de Rham上同调群彼此同构。
所以下同调群的几何意思就是圈和边的差别。公式上下圈和边都可能有几十万维,但最终区别只有几维,在于有多少handle。
下面解释用图例直观展现同伦和同调不同之处,同伦群比同调群多了很多信息。
接着介绍单纯映射定理,联系复形的多面体之间的一类重要映射。它是从复形 K 的多面体|K|到复形 L 的多面体|L|的连续映射,任何连续映射在某种意义下可用它逼近。该定理工程上经常用,目前电影效果不是很好,有部分原因是单纯映射没做好。
代数拓扑的目的是将拓扑范畴的问题转换成代数范畴的问题,用代数方法加以解决。最为基本的问题之一就是判断两个拓扑空间是否同胚。在理想情形下,我们为每一个空间配上一系列群结构,如果这些群彼此同构,则空间拓扑同胚。但是,目前代数拓扑的方法还没有到达这一程度。同调群同构只能推出空间同伦等价。伦型等价远远弱于拓扑等价。经过几十年的努力,初心本想在拓扑空间上用拓扑同胚不变量作为代数表示,结果变成了用同调群来处理,信息损失不少。 同调论的基本方法是将流形三角剖分,然后将子流形表示成单形的线性组合,所有的子流形构成线性空间。将拓扑算子(边缘算子)表示成线性算子(矩阵),用线性代数的方法来获取拓扑信息。同调方法将低秩、稀疏,高度非线性的拓扑性质变换成高维空间的线性运算,非常具有启发意义。另外如何更优的三角剖分,请参照其他专题课题。
(作者注:随着上同调的被定义,原先讲的同调群一般指下同调群。)
介绍同调群的应用。
莱布尼茨Number回答了存在不动点问题,江泽涵的研究回答了不动点有多少个的问题。理论都很成熟了,还是需要有心人把代码编出来,哈哈哈。
接着介绍同调群的应用。
拓扑去噪应用
我们用 CT 断层扫描技术获取直肠切面图像,经过曲面复建得到直肠曲面。由于图像分割的误差,复建的曲面有很多虚假的亏格(环柄)。在实际应用中,我们需要检测这些虚假亏格。这些环柄非常微小,用肉眼无法直接检测。唯一的方法就是通过计算拓扑方法(同调群理论)得到,这往往依赖于曲面的环柄圈和隧道圈的算法。得到这些虚假环柄之后,我们将它们沿着环柄圈切开,然后再填补洞隙来去除拓扑噪声。
介绍上同调
进入上同调群学习,和万有覆盖空间一样,是比较难的章的章节。从基本定理、基本构造两方面,与下同调比较。
上同调的引入就是度量拓扑空间的洞,同调是比同伦更为有力的工具。
下同调理论的要义是考察流形上所有的封闭曲线(圈),和所有曲面片的边缘(边),所有的边必为圈,反之不对,存在不是边的圈,因此圈和边的差别就是流形的下同调。
我们用场论来直观解释上同调的思想:上同调理论的本质是考察流形上所有旋量为零的切矢量场(无旋场)和所有函数的梯度场。梯度场必为无旋场,反之不对。存在不是梯度场的无旋场,因此无旋场和梯度场的差别就是流形的上同调。
上同调可以看作是一种对拓扑空间赋予代数不变量的方法,但其代数结构比同调更为精炼。上同调源于同调的构造过程的代数对偶。通俗意义上讲,上链的基本意义是为同调的链赋予某种“量”。
上同调运算包括艾达尔上同调(Étale cohomology),德拉姆上同调(de Rham cohomology),李代数上同调,伽罗瓦上同调,霍赫希尔德同调。
如何计算上同调,引出Stokes定理。
讲解了工业界常用的样条定理,设计时没考虑拓扑问题,存在 C^2 不光滑问题。用上同调理论能很好解决该拓扑障碍。
庞加莱-霍普夫定理 Poincare-Hopf,微分流行上向量场零点的指标等于这个微分流行的欧拉示性数。
指标,可以形象的理解为向量场在某点的绕圈数,绕几圈这个数就是“几”。欧拉示性数,等于顶点数+面数﹣棱数。实际上欧拉示性数可以拓展到一般的拓扑空间上,并且是一个非常重要的拓扑不变量,可以通过很多数学方法得到,譬如可以通过对微分流形进行三角剖分得到。
现实中有个神奇而又深刻的定理:毛球定理,实际上它是庞加-莱霍普夫( Poincare - Hopf )定理的一个非常简单特例。毛球定理说的是对于一个表面垂直布满毛发的圆球,无法把所有的毛发抚平。当然,这是非常形象的描述,并不太严格,用严格的数学语言来说,二维欧式球面上不存在处处非零的光滑向量场,也就是说球面上的非零向量场必定有零点,而在这个零点处,“毛发”就无法被捋平,因为被“捋平”就意味着没有零点。这样,“毛球定理”就在数学上得到了完美的解释。
利用这个定理可以得到许多有趣的推论,一个表面垂直布满毛发的圆球上,不可能把所有毛发抚平;你不可能给一个毛茸茸的毛球顺毛。大自然造物也遵循这个定理,所以人头发在生长时就会有漩涡状的发旋。当然现实中去掉这个发旋倒是也简单,把“零向量”的地方搞成一条线譬如中分,或者干脆处理为零譬如光头党。O(∩_∩)O哈哈~
事实上所谓的这个“毛球定理”还可以解释很多的物理现象。我们的地球就可以看成一个球体,地球表面的风速和风向也都是连续的。我们做出风速的向量场,根据这个定理必然会存在风速为零的地方,这也就从理论上肯定了气旋的产生。风速为零的地方也就是气旋的风眼。事实上,这种与拓扑学有关的自然现象还有很多。比如你的耳机线就很容易打结,缠在一起难以解开,但是如果把线的首尾两端连接起来构成一个闭环,就可以有效减少打结的情况。具体的原理大家也可以进行一些更为深入的思考。
该定理给出了零点和欧拉示性数之间关系,把流形上的向量场和拓扑不变量联系了起来。庞加莱-霍普夫定理最初由庞加莱得到二维的情况,之后霍普夫推广到高维情况。
证明庞加莱-霍普夫定理,更进一步熟悉上同调理论。
上同调算法实现,介绍算法前半部分,下面计算偏微分方程,引入调和场。
调合场
介绍调和场,庞加莱对偶,定义*w,w。
为了计算调和 1-形式 Harmonic 1-form,引出一个大定理,Hodge定理。把PDE方程变成对称矩阵。具体算法介绍下图再述。
先介绍一些其他基础知识。
阿蒂亚-辛格指标定理(Atiyah-Singer Index Theorem)是微分几何和拓扑学中的一个定理。此定理由英国数学家迈克尔·阿蒂亚与美国数学家艾沙道尔·辛格于1962年给出第一个证明。 该定理断言,对于紧的可定向的流形上的线性椭圆微分算子,其解析指标等于拓扑指标。几何和拓扑学中的许多大定理,包括黎曼-罗赫定理(Riemann-Roch Theorem)、希兹布鲁赫符号差定理(Hirzebruch's Signature Theorem)、高斯-博内-陈定理(Gauss-Bonnet-Chern Theorem)都是它的特殊情况,指标定理在理论物理学中亦有应用。
Hodge定理:曲面上所有无旋无散矢量场(旋度为 0,散度为 0 的场)成群,此群和曲面的上同调群同构,这就是所谓的霍奇(Hodge)理论。Hodge定理可以直接推广为黎曼面上的黎曼-罗赫定理,进而更为广泛的指标定理。
直观而言,我们考察曲面上的切向量场,如果这个向量场光滑得无以复加,那么这个向量场被称为是调和场(Harmonic Field)。所有的调和 k- 形式构成群,调和 k- 形式群和流形的 k 阶上同调群同构。
有时把Hodge定理称为霍奇分解定理,曲面上任意一个光滑切向量场,可以被唯一地分解为三个向量场:梯度场、散度场和调和场。霍奇分解经常被用于光滑化一个矢量场,将一个不可积矢量场变得可积。
该理论进一步揭示了分析与拓扑之间的深刻联系,给当代流形分析的整体研究产生了巨大影响。这一定理在图形学、计算机视觉和网络中,应用非常广泛。
由于Hodge的贡献,我们再介绍一些内容:
霍奇猜想,一个非奇异射影代数簇上的每一个(一定类型的)调和微分形式都是代数闭链的上同调类的一个有理组合。
微积分通常是在二维平面或者球面上,可以推广到各种各样更为一般的簇上。霍奇猜想涉及的是推广到一个非奇异射影代数簇上的微积分。它对某种类型的抽象对象作出了一个断言,我们把这种抽象对象称为H对象,如果我们从某种类型的簇着手并在其上做某种微积分,就会产生H对象。当我们用微积分去定义一个对象时,定义出来的对象从任何意义上说都不一定是"几何的"。霍奇猜想说,H对象对刚才这句话来说是个例外。虽然它们本身可能不是几何对象,但它们能以一种相当简单的方式由几何对象构建起来。在这个猜想的术语中,H对象就是代数闭链的上同调类的一个有理组合。这就是说,任何H对象都能以一种纯粹代数的方式由几何对象构建起来。
我们可以从代数簇上沿着广义路径的积分着手来提出霍奇猜想。由于对路径进行变形仍能保持这种积分的值不变,因此你可以认为这种积分是定义在路径类上的。霍奇猜想提出,如果某些这样的积分为零,那么在这个路径类中存在着一条能用多项式方程描述的路径。非奇异复代数簇的代数拓扑和多项式方程所表述的几何有关联。
霍奇猜想的作用是给专家们提供某种能用来分析H对象的强有力的数学结构。这在许多现代数学中十分重要,数学家不断在寻找对象上的新结构,或者是寻找从一个领域到另一个领域的联系,以使他们能把来自一个领域的方法加以改造,运用于另一个领域。霍奇猜想、费马大定理和黎曼猜想成为广义相对论和量子力学融合的 m 理论载体和工具。
霍奇猜想的证明将在代数几何、分析和拓扑学这三个学科之间建立起一种基本的联系。
当今黎曼假设、庞加莱猜想、霍奇猜想、贝赫和斯维讷通-戴尔猜想、纳维叶―斯托克斯方程、杨―米尔理论、P问题对NP问题被称为21世纪世界七大数学难题。
计算holomorpic 1-form的算法如上,现在主要需要计算:
为方便计算,引出在等温坐标下 *w 和 d 的定义。
定义了全纯1-形式计算公式,为了计算该实部与虚部,先介绍复变函数,其形式如下:
在其定义域上处处解析,也就是处处可导。在我们遇到的情形中解析函数的实部和虚部满足柯西——黎曼条件。柯西-黎曼微分方程是提供了可微函数在开集中为全纯函数的充要条件的两个偏微分方程。因为可微,所以就列出线性主部表出的一个式子,实部对实部,虚部对虚部。
而咱们又别于复变函数的定义为:
保角变换又叫保角映射conformal transformation。设f(z)是区域 D 到 G 的双射(既是单射又是满射),且在 D内的每一点都具有保角性质,则称 f(z) 是区域 D 到 G 的保角映射,也称为保角变换或者共形映射。即图形在变换前后,其形状产生了旋转和伸缩,但是两条曲线之间的夹角保持不变。
以前计算保角变换都是基于复变函数,现在将代数拓扑、微分几何和调和理论充分地结合在一起,不但可以解决平面问题,也可以解决曲面问题。
例:以上为亏格一的曲面保角变换到平面的共形计算方法。
补充介绍一些复分析几何的理论和应用,其核心是计算全纯1-形式。
工业应用案例分享
以下主要摘自《老顾谈几何》总结性内容 2022计算共形几何课程总结_腾讯新闻
图形渲染:高效逼真的图形渲染强烈依赖于纹理贴图和法向贴图技术,而这些技术归结为曲面参数化方法。共形几何的单值化定理可以将具有复杂拓扑和几何的曲面映射到平面区域,并且这种映射局部保形,没有引入几何畸变。
几何畸变可以分成两类:局部形状的畸变和局部面积元的畸变。如果使得局部形状被保持,即映射局部是相似变换,但是相似比逐点不同,所得的映射是共形映射(conformal mapping),由共形几何理论来研究;如果使得面积元被保持,则所得映射为最优传输映射,由最优传输理论来刻画。
近期虚幻引擎5的Nanite虚拟几何技术将渲染效率提高了几个数量级,使得元宇宙中超大场景的实时渲染成为可能。而虚拟几何技术的核心是将不规则的三角网格转换成规则的几何图像,而这种转换依赖于曲面全局参数化。迄今为止,计算共形几何是唯一的可行方法。
几何建模:传统的机械几何建模是将简单的基本形状进行布尔运算得到复杂几何实体。比较现代的方法是直接扫描三维实体得到稠密点云,然后用SLAM技术将点云融合,再用数字几何技术重建三维曲面。初始重建的曲面往往具有大量的拓扑和几何噪音,需要用计算拓扑的方法去除拓扑噪音,用计算几何的方法去除几何噪音,再用共形几何方法进行三角剖分,得到高质量三角网格。高质量的网格可以用于后端的CAE数值模拟仿真,也可以应用于CAM,直接三维打印出来。传统几何建模领域中,最终曲面都被表示成高阶光滑的样条曲面,例如B-Spline,NURBS 和 T-样条曲面。通过共形几何的方法,我们可以将三角网格曲面转换成样条曲面。
几何约束求解:在工程实践中,我们往往需要求解带有几何约束的问题。计算共形几何给出系统性的方法来解决这类问题。例如扎哈设计的大兴国际机场的建筑大量采用曲面的叶状结构概念,而曲面的叶状结构等价于黎曼面上的全纯二次微分,归结为在曲面上特定的上同调类中求非线性椭圆型偏微分方程。计算共形几何给出精确的算法, 可以计算复杂曲面上所有的叶状结构。
再如,近些年来,拓扑优化技术发展迅猛。传统的拓扑优化设计都是在欧氏空间中施行,应用共形几何,我们可以将欧氏空间的方法直接推广到曲面上,在曲面上求解偏微分方程。例如,我们可以设计具有负泊松比的超材料,用于防弹面罩设计。
网格剖分:在CAE数值模拟仿真中,网格生成部分经常占据70%以上的时间和成本,因此网格生成具有根本的重要性。传统的基于Delaunay Refinment的平面三角剖分算法非常成熟。通过共形映射,我们将曲面映到平面,同时这个映射保角,因此可以将平面高质量的三角剖分拉回到曲面上,生成曲面的高质量三角网格。
曲面的结构化网格生成更加困难,其中关键在于网格奇异点构型的选取。长期以来,曲面四边形网格生成都是依赖于有经验的工程师手工调整。我们发现四边形网格等价于黎曼面上的亚纯四次微分,其奇异点等价于主除子,从而满足Abel方程。因此,计算共形几何方法为结构化网格生成奠定了理论基础,给出了高效算法。
CAE高性能数值计算:计算共形几何提供了完备的理论和算法在曲面上高效、高精度求解线性、非线性偏微分方程,得到各种函数和张量。这些方程的求解方法可以直接应用于工程领域。计算共形几何提供了曲面Ricci流算法,可以通过高斯曲率来反解黎曼度量,这是目前唯一的方法能够构造黎曼度量。所有的曲面都存在一个与初始度量共形等价的度量,并且诱导常值曲率,常数为+1,0,或者-1取决于曲面拓扑。通过单值化,我们可以将任何曲面上的偏微分方程转化为平面区域的偏微分方程。例如,曲面上的椭圆型偏微分方程例如热力学、弹性力学中的Lapalce方程,Poisson方程,都在共形变换下不变,从而转化成平面区域的类似方程,应用成熟的平面PDE方法求解,提高了计算效率。还有曲面上的全纯微分,用于六面体网格生成等。
几何(图)数据库:Klein的Erlangen纲领指出,不同的几何研究不同变换群下的不变量。我们可以将这些不变量作为曲面的“指纹”,将几何曲面分类,实现几何数据库的索引和几何搜素引擎。计算共形几何算法提供了所有的几何拓扑不变量,例如拓扑中的亏格、同伦同调群、曲面自旋结构;共形几何中的周期矩阵,Fuchsian群;黎曼几何中的黎曼度量(共形因子),Laplace的谱,热核;微分几何中的主曲率、平均曲率。用这些不变量,我们可以将曲面由粗到精,逐步分类。同时,计算共形几何提供了计算曲面之间各种映射的方法,比如极小化几何畸变的Teichmuller映射方法,从而可以建立曲面间精确的对应关系,进行精细的比较,从而计算曲面间的距离。
数据转换:几何数据的常见数据表示包括点云,图,非结构化网格和样条。通过如上的讨论,我们看到共形几何可以将这些表示进行转换。
数据模型驱动:共形几何方法可以和深度学习方法结合,用于几何生成模型。首先,通过全局参数化,我们将曲面转换成几何图像,从而可以直接应用各种卷积网络。同时,我们也可以用几何方法来解释深度学习方法,指导新型学习模型的设计。例如,我们知道深度学习的主要任务是学习流形上的概率分布,其中概率分布的学习算法是基于最优传输理论。由蒙日安培方程的正则性理论,传输映射不一定连续,经常存在奇异集合,而深度神经网络只能学习连续映射,这一本质矛盾造成了模式坍塌(mode collapse)。由此,我们基于最优传输映射的几何变分法,设计了AE-OT模型,可以避免模式坍塌。
本文介绍了邱先生和顾教授在计算共形几何领域的一些重大理论创新,并分享了其团队在工程领域独一无二的算法。