【UnityShader入门精要学习笔记】第四章(3)矩阵的性质
![]()
本系列为作者学习UnityShader入门精要而作的笔记,内容将包括:
- 书本中句子照抄 + 个人批注
- 项目源码
- 一堆新手会犯的错误
- 潜在的太监断更,有始无终
总之适用于同样开始学习Shader的同学们进行有取舍的参考。
文章目录
- 复习
-
- 知识点复习
-
- 向量加减
- 向量乘除
- 向量模长
- 向量归一化
- 向量点乘
- 向量叉乘
- 练习题答案
- 矩阵
-
- 矩阵的定义
- 矩阵和向量的联系
- 矩阵运算
-
- 矩阵加减
- 矩阵数乘
- 矩阵乘法
- 一些特殊的矩阵
-
- 方阵
- 对角矩阵
- 单位矩阵
- 转置矩阵
- 逆矩阵
- 正交矩阵
- 练习题
(该系列笔记中大多数都会复习前文的知识,特别是前文知识非常重要的时候,这是为了巩固记忆,诸位可以直接通过目录跳转)
复习
知识点复习
上节我们学习了点和向量,以及向量的基本运算法则
点(point) 是n维空间中的一个位置,而向量(vector) 是n维空间中的一个有向线段,有模长(magnitude) 和方向(direction) 两种属性。
在坐标空间下,我们往往可以把向量和点等同起来。
向量加减
假设有向量a和向量b,则:
a → + b → = ( a x + b x , a y + b y ) a → − b → = ( a x − b x , a y − b y ) \overrightarrow a+\overrightarrow b=(a_x+b_x,a_y+b_y) \newline \overrightarrow a-\overrightarrow b = (a_x-b_x,a_y-b_y) a+b=(ax+bx,ay+by)a−b=(ax−bx,ay−by)
在几何上我们可以使用三角法则得出向量运算结果
向量乘除
我们可以用一个标量来对向量进行乘除:
k v → = ( k x , k y , k z ) v → / k = ( x k , y k , z k ) k\overrightarrow v=(kx,ky,kz) \newline \overrightarrow v/k=(\frac{x}{k},\frac{y}{k},\frac{z}{k}) kv=(kx,ky,kz)v/k=(kx,ky,kz)
向量乘除本质上是对向量的拉伸变换
向量模长
模长公式:
∣ v → ∣ = x 2 + y 2 + z 2 |\overrightarrow v| = \sqrt{x^2+y^2+z^2} ∣v∣=x2+y2+z2
简单的计算,因为几何上直观来看就是运用了勾股定理。
向量归一化
给定任意非零向量 v → \overrightarrow v v,将其归一化为模长为1的单位向量,归一化公式为:
v ^ = v → ∣ v → ∣ \hat v = \frac{\overrightarrow v}{|\overrightarrow v|} v^=∣v∣v ,即该向量除以其模长

归一化的单位向量模长为1,因此所有归一化向量可以构成一个单位圆。其落点都在单位圆的圆周上。
向量点乘
向量点乘
向量的点积公式如下:
a → ⋅ b → = ( a x , a y , a z ) ⋅ ( b x , b y , b z ) = a x b x + a y b y + a z b z \overrightarrow a \cdot \overrightarrow b =(a_x,a_y,a_z)\cdot(b_x,b_y,b_z)=a_xb_x+a_yb_y+a_zb_z a⋅b=(ax,ay,az)⋅(bx,by,bz)=axbx+ayby+azbz
点积满足以下性质:
a → ⋅ b → = b → ⋅ a → ——交换律 \overrightarrow a \cdot \overrightarrow b = \overrightarrow b \cdot \overrightarrow a——交换律 a⋅b=b⋅a——交换律
( k a ) ⋅ b = a ⋅ ( k b ) = k ( a ⋅ b ) ——结合律 (ka) \cdot b = a \cdot(kb) = k(a \cdot b) ——结合律 (ka)⋅b=a⋅(kb)=k(a⋅b)——结合律
a ⋅ ( b + c ) = a ⋅ b + a ⋅ c ——分配律 a \cdot (b+c) = a \cdot b + a \cdot c ——分配律 a⋅(b+c)=a⋅b+a⋅c——分配律
v ⋅ v = v x 2 + v y 2 + v z 2 = ∣ v ∣ 2 v \cdot v = v_x^2 + v_y^2 +v_z^ 2 = |v|^2 v⋅v=vx2+vy2+vz2=∣v∣2

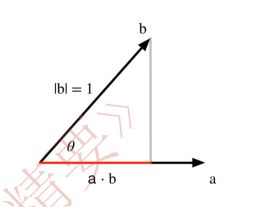
点积其实本质上计算的是投影与向量的乘积。对于 v → ⋅ w → \overrightarrow v \cdot \overrightarrow w v⋅w而言,其计算结果实质上是 w → \overrightarrow w w的投影长度 乘以 ∣ v → ∣ |\overrightarrow v| ∣v∣
根据两个向量之间的夹角,点积的符号也不同,若夹角小于90°则结果>0,若等于90°则=0,若大于90°则<0
(简单来说, [ v x v y ] ⋅ [ w x w y ] \begin{bmatrix}v_x\\ v_y\end{bmatrix} \cdot \begin{bmatrix}w_x\\ w_y\end{bmatrix} [vxvy]⋅[wxwy]实质上与矩阵乘法 [ v x v y ] [ w x w y ] \begin{bmatrix}v_x v_y\end{bmatrix} \begin{bmatrix}w_x\\ w_y\end{bmatrix} [vxvy][wxwy]相等,而后者计算结果实际上是将二维矩阵w应用线性变换v使其降维到了一维空间,这个一维空间就是我们用于投影的数轴,降维后的结果就是投影,所以向量点积本质上就是一个将矩阵从二维变换到一维的线性变换。)
从三角函数上看,点积公式还可以表示为下列形式:
a ⋅ b = ∣ a ∣ ∣ b ∣ c o s θ a \cdot b = |a||b|cos\theta a⋅b=∣a∣∣b∣cosθ
(其实还是投影乘以模长,投影是 ∣ b ∣ c o s θ |b|cos\theta ∣b∣cosθ,模长是 ∣ a ∣ |a| ∣a∣)
投影还有一些其他的性质:
向量叉乘
另一个重要的运算是向量的叉乘(cross product) ,也称为外积(outer product) 。
叉乘的公式是:
a × b = ( a x , a y , a z ) × ( b x , b y , b z ) = ( a y b z − a z b y , a z b x − a x b z , a x b y − a y b x ) a × b =(a_x,a_y,a_z) ×(b_x,b_y,b_z) = (a_yb_z - a_zb_y,a_zb_x-a_xb_z,a_xb_y-a_yb_x) a×b=(ax,ay,az)×(bx,by,bz)=(aybz−azby,azbx−axbz,axby−aybx)
叉乘满足以下性质:
a × b = − ( b × a ) ——交换律 a × b = -(b×a) ——交换律 a×b=−(b×a)——交换律
( a × b ) × c ≠ a × ( b × c ) (a × b) × c \ne a × (b × c) (a×b)×c=a×(b×c)
虽然很难记,但如果用线性代数的角度去考虑就清晰许多:

实际上叉乘就是加上一列基向量构成一个新矩阵,并计算该矩阵的行列式。
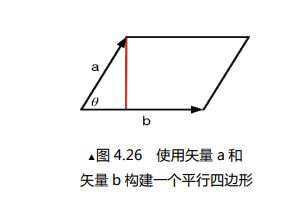
记住一个简单的结论就是,两个向量叉乘,最终会得到一个新向量,这个新向量的长度是 v , w v,w v,w向量构成的平行四边形的面积,而新向量的方向,由原坐标系指定,且垂直于这个平行四边形。如果你使用右手坐标系,就举起右手,反之使用左手,使得任意两根手指与 v , w v,w v,w对齐,剩下那根的方向就是新向量的方向。
这个叉乘出来的向量的模长由于和平行四边形面积一致,所以我们也可以得到叉乘向量的模长公式:
∣ a × b ∣ = ∣ a ∣ ∣ b ∣ s i n θ |a × b| = |a||b|sin\theta ∣a×b∣=∣a∣∣b∣sinθ (平行四边形面积=底 * 高)
叉乘最常见的应用就是计算垂直于一个平面、三角形的向量,还可以用于判断三角面片的朝向。
练习题答案
1.判断题
(1)错误,向量由方向和模长两个要素构成
(2)正确
(3)错误,叉乘运算规则是与左右手系无关的, 但其在右手坐标系的结果是符合右手定则的, 在左手坐标系的结果是符合左手定则的(如果根据上节的行列式就好理解了,基向量 i ^ , j ^ , k ^ \hat i ,\hat j,\hat k i^,j^,k^都是基于原坐标系的,无论左右手坐标系,最后计算的结果都是相同的,只是在不同坐标系空间上,新产生的那个向量的位置会发生改变)
(1) 62 \sqrt {62} 62
(2)(12.5,10,25)
(3)(1.5,2)
(4) ( 5 13 , 12 13 ) (\frac{5}{13},\frac{12}{13}) (135,1312)
(5) ( 1 3 , 1 3 , 1 3 ) (\frac{1}{\sqrt 3},\frac{1}{\sqrt 3},\frac{1}{\sqrt 3}) (31,31,31)
(6)(10,9)
(7)(-6,1,2)
d = ∣ ( 10 , 13 , 11 ) − ( 2 , 1 , 1 ) ∣ = 64 + 144 + 100 = 308 d = |(10,13,11)-(2,1,1)| = \sqrt{64+144+100}=\sqrt{308} d=∣(10,13,11)−(2,1,1)∣=64+144+100=308
(1)75
(2)13
(3)13
(4)(-9,-13,7)
(5)(9,13,-7)(其中(5)与(4)正好位置互换,因此 a × b = − ( b × a ) a × b =-(b× a) a×b=−(b×a))
(1) a ⋅ b = ∣ a ∣ ∣ b ∣ c o s θ = 4 ∗ 6 ∗ 1 2 = 12 a \cdot b = |a||b|cos\theta = 4 * 6 * \frac{1}{2} = 12 a⋅b=∣a∣∣b∣cosθ=4∗6∗21=12
(2) ∣ a × b ∣ = ∣ a ∣ ∣ b ∣ s i n θ = 4 ∗ 6 ∗ 3 2 = 12 3 |a×b| = |a||b|sin\theta = 4* 6 * \frac{\sqrt{3}}{2} =12\sqrt{3} ∣a×b∣=∣a∣∣b∣sinθ=4∗6∗23=123
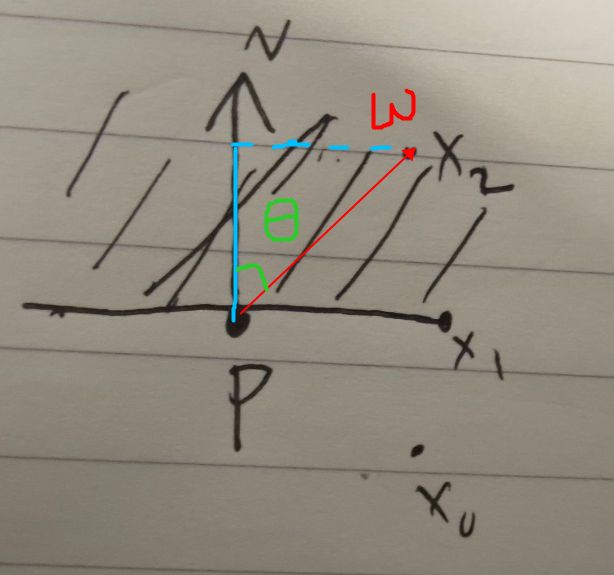
(1)想要判断玩家在NPC的前方还是后方,也就是判断玩家相对于NPC的方向,以向量 v v v表示前方。
如图所示,那么以向量v为y轴,p为原点建立的直角坐标系上,第一象限和第二象限都可以视为前方。图中三个示例点x,只有 x 2 x_2 x2是前方的点。
也就是说只需要连接点p到点x,构建向量w。当向量w和向量v的夹角 θ \theta θ小于90°时,则正面x在p的前方。
做w到v方向上的投影,其实就是点积 w ⋅ v > 0 w \cdot v >0 w⋅v>0时,证明玩家在npc的前方。同理,当 w ⋅ v = 0 w \cdot v =0 w⋅v=0证明玩家与npc在水平方向,当 w ⋅ v < 0 w \cdot v <0 w⋅v<0证明玩家在npc后方。
(2)带入点 p = ( 4 , 2 ) , v = ( − 3 , 4 ) , x = ( 10 , 6 ) p=(4,2),v=(-3,4),x=(10,6) p=(4,2),v=(−3,4),x=(10,6)来验证答案
v ⋅ w = ( − 3 , 4 ) ⋅ ( 6 , 4 ) = − 2 < 0 v\cdot w=(-3,4)\cdot(6,4)=-2<0 v⋅w=(−3,4)⋅(6,4)=−2<0,此时玩家在npc后方
(3)npc的视野角度为 ϕ \phi ϕ,则左右能看到的角度为 ϕ 2 \frac{\phi}{2} 2ϕ,那么只需根据公式求出夹角 θ < = ϕ 2 \theta <= \frac{\phi}{2} θ<=2ϕ即可证明在视野范围内。
则 v ⋅ w = ∣ v ∣ ∣ w ∣ c o s θ , 所以 θ = a r c c o s ( v ⋅ w ∣ v ∣ ∣ w ∣ ) < = ϕ 2 v \cdot w = |v||w|cos\theta,所以\theta = arccos(\frac{v\cdot w}{|v||w|})<= \frac{\phi}{2} v⋅w=∣v∣∣w∣cosθ,所以θ=arccos(∣v∣∣w∣v⋅w)<=2ϕ 即可(或者 c o s θ < = c o s ϕ 2 ) cos\theta <= cos\frac{\phi}{2}) cosθ<=cos2ϕ)
(4)现在NPC只能看到固定距离内的对象,则以该距离为半径,P点为圆心画圆,可见范围即为该y正半轴上半圆与视野夹角范围的相交面积。
只需证明向量w的模长小于等于该距离即可。
7.如何证明三个顶点方向是顺时针还是逆时针,首先要明确,顶点方向是顺时针还是逆时针和p1的位置以及p2的位置没有关系,只和p3的位置有关系
为什么这么说?假设p1,p2位置已知,我们任取两个点作为p1,p2,以p1为起点,连接p2为向量v。再任取一点作为p3,连接p1,p3作为向量w。发现在向量v固定的情况下,顶点的顺时针还是逆时针关系完全由向量w的位置(p3的位置)决定。
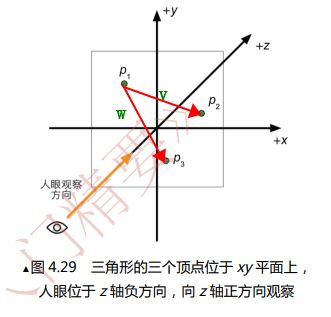
观察原图,不难发现,原图的坐标系为左手坐标系。也就是说,如果想要证明该面片是正面(也就是正面朝向z轴负方向,意味着叉乘结果产生的新向量指向z轴负方向,运用左手法则,握住z轴负方向,发现此时四指方向为顺时针),只需证明面片的叉乘向量指向z轴负方向,也就是证明叉乘结果<0即可。
因此问题转化为:若向量w和v的叉乘结果<0,则顶点顺序为顺时针,反之若叉乘结果>0则为逆时针。
为了方便计算,我们直接把点p1放在原点,设 p 1 = ( 0 , 0 , 0 ) , p 2 = ( x 2 , y 2 , 0 ) , p 3 = ( x 3 , y 3 , 0 ) p_1=(0,0,0),p_2=(x_2,y_2,0),p_3 = (x_3,y_3,0) p1=(0,0,0),p2=(x2,y2,0),p3=(x3,y3,0)
所以 v = ( x 2 , y 2 , 0 ) , w = ( x 3 , y 3 , 0 ) v=(x_2,y_2,0),w=(x_3,y_3,0) v=(x2,y2,0),w=(x3,y3,0),因此:
v × w = ( 0 , 0 , x 2 y 3 − x 3 y 2 ) , v × w=(0,0,x_2y_3-x_3y_2), v×w=(0,0,x2y3−x3y2),
因此若 x 2 y 3 − x 3 y 2 < 0 , 则为顺时针,反之若 x 2 y 3 − x 3 y 2 > 0 则为逆时针 x_2y_3-x_3y_2<0,则为顺时针,反之若x_2y_3-x_3y_2>0则为逆时针 x2y3−x3y2<0,则为顺时针,反之若x2y3−x3y2>0则为逆时针
那 x 2 y 3 − x 3 y 2 = 0 x_2y_3-x_3y_2 =0 x2y3−x3y2=0呢?拜托大哥,那 p 1 , p 2 , p 3 p_1,p_2,p_3 p1,p2,p3不就在同一条直线上了吗,根本没法构成三角形的。
矩阵
你可能注意到,在前文我已经提到了矩阵,行列式等线性代数中的数学概念,因为如果你想学习计算机图形学的相关知识,我默认诸位读者已经了解线性代数的基本知识。也正因如此我才在开篇就极力推荐大家先去观看线性代数的本质一课。
因此,我接下来只会简单介绍矩阵的一些性质。再结合线性代数的本质一课中所学的内容简单解说。
矩阵的定义
矩阵(matrix) 是由m行n列标量组成的数组,例如一个3行四列的矩阵,我们称为一个 3 × 4 3×4 3×4的矩阵:
M = [ m 11 m 12 m 13 m 14 m 21 m 22 m 23 m 24 m 31 m 32 m 33 m 34 ] M=\begin{bmatrix}m_{11} &m_{12} &m_{13}& m_{14}\\ m_{21}&m_{22}&m_{23}&m_{24}\\ m_{31}&m_{32}&m_{33}&m_{34} \end{bmatrix} M= m11m21m31m12m22m32m13m23m33m14m24m34
特别的,若矩阵行数=列数,我们称其为方阵
矩阵和向量的联系
向量也可以用矩阵的形式来表示,例如点 p = ( x , y , z ) p=(x,y,z) p=(x,y,z)我们可以表示为:
p = [ x y z ] p=\begin{bmatrix}x\\ y\\ z \end{bmatrix} p= xyz
我们将其称之为 n × 1 的列向量 n × 1的列向量 n×1的列向量
或者也可以表示为:
p = [ x y z ] p=\begin{bmatrix}x&y& z \end{bmatrix} p=[xyz]
称为 1 × n 的行向量 1×n的行向量 1×n的行向量
但实际上学过线性代数的本质的话,我们更认同使用列向量表示一个向量,因为行通常代表着维度的数量。因此,一个矩阵实际上也可以视为向量的集合,例如上述的三行四列矩阵M,就代表了四个三维向量的集合。
矩阵运算
矩阵加减
矩阵加减很简单,由于矩阵是向量的集合,因此我们可以将其视为多个向量的加减,仅需要保证两个矩阵的行列数一致即可:
A = [ a 11 a 12 a 13 a 14 a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 ] B = [ b 11 b 12 b 13 b 14 b 21 b 22 b 23 b 24 b 31 b 32 b 33 b 34 ] A + B = [ a 11 + b 11 a 12 + b 12 a 13 + b 13 a 14 + b 14 a 21 + b 21 a 22 + b 22 a 23 + b 23 a 24 + b 24 a 31 + b 31 a 32 + b 32 a 33 + b 33 a 34 + b 34 ] A=\begin{bmatrix}a_{11} &a_{12} &a_{13}& a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34} \end{bmatrix} \newline B=\begin{bmatrix}b_{11} &b_{12} &b_{13}& b_{14}\\ b_{21}&b_{22}&b_{23}&b_{24}\\ b_{31}&b_{32}&b_{33}&b_{34} \end{bmatrix} \newline A+B=\begin{bmatrix}a_{11}+b_{11} &a_{12}+b_{12} &a_{13}+b_{13}& a_{14}+b_{14}\\ a_{21}+b_{21}&a_{22}+b_{22}&a_{23}+b_{23}&a_{24}+b_{24}\\ a_{31}+b_{31}&a_{32}+b_{32}&a_{33}+b_{33}&a_{34}+b_{34} \end{bmatrix} A= a11a21a31a12a22a32a13a23a33a14a24a34 B= b11b21b31b12b22b32b13b23b33b14b24b34 A+B= a11+b11a21+b21a31+b31a12+b12a22+b22a32+b32a13+b13a23+b23a33+b33a14+b14a24+b24a34+b34
减法同理
矩阵数乘
矩阵的数乘也很简单,也可以视为对向量集合的数乘:
k M = M k = k [ m 11 m 12 m 13 m 14 m 21 m 22 m 23 m 24 m 31 m 32 m 33 m 34 ] = [ k m 11 k m 12 k m 13 k m 14 k m 21 k m 22 k m 23 k m 24 k m 31 k m 32 k m 33 k m 34 ] kM=Mk=k\begin{bmatrix}m_{11} &m_{12} &m_{13}& m_{14}\\ m_{21}&m_{22}&m_{23}&m_{24}\\ m_{31}&m_{32}&m_{33}&m_{34} \end{bmatrix}= \begin{bmatrix}km_{11} &km_{12} &km_{13}& km_{14}\\ km_{21}&km_{22}&km_{23}&km_{24}\\ km_{31}&km_{32}&km_{33}&km_{34} \end{bmatrix} kM=Mk=k m11m21m31m12m22m32m13m23m33m14m24m34 = km11km21km31km12km22km32km13km23km33km14km24km34
矩阵乘法
矩阵和矩阵的相乘相对就麻烦了,本质上来说需要遵循一个规则才能相乘:
A 为 r × n 的矩阵, B 为 n × m 的矩阵,则 A B 结果为 r × m 的矩阵 A为r×n的矩阵,B为n×m的矩阵,则AB结果为r×m的矩阵 A为r×n的矩阵,B为n×m的矩阵,则AB结果为r×m的矩阵
就是前一个矩阵的行数要和后一个矩阵的列数相同。
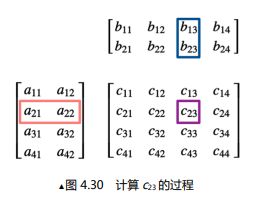
以上图为例,矩阵AB的结果计算出矩阵C,其中 c 11 = a 11 ∗ b 11 + a 12 ∗ b 21 c_{11}=a_{11}*b_{11}+a_{12}*b_{21} c11=a11∗b11+a12∗b21, c 12 = a 11 ∗ b 12 + a 12 ∗ b 22 c_{12}=a_{11}*b_{12}+a_{12}*b_{22} c12=a11∗b12+a12∗b22…以此类推,就是使用被乘数的行向量与乘数的列向量相乘。
矩阵乘法有以下性质:
- 矩阵乘法不满足交换律: A B ≠ B A AB \ne BA AB=BA
- 矩阵乘法满足结合律: ( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)
在学习了线性代数的本质之后,对于矩阵乘法我们可以在几何上更直观的理解:
其中被乘数代表了对基向量应用的线性变换之后得到的矩阵,我们通过将该矩阵乘上另一个向量来对该向量应用此变换。而乘数代表了一个向量的集合。因此矩阵相乘在几何上的含义就是:
对一个矩阵集合中的所有向量(乘数B)应用一种线性变换(被乘数A)之后得到的新的向量集合(AB)
一些特殊的矩阵
方阵
方阵指的是行列数相等的矩阵。在三维渲染里最常用的方阵是3×3和4×4的
方阵具有一些特殊的性质,例如方阵可以计算行列式(上节提到了行列式公式)。
行列式的值代表了应用某线性变换的矩阵其基向量构成的面积大小是单位面积的多少倍(三维下同理面积替换为体积)。
(例如一个二维方阵 [ 1 0 0 1 ] \begin{bmatrix}1 &0\\ 0&1\\ \end{bmatrix} [1001],其基向量构成的单位面积是1,应用线性变换变为矩阵 [ 2 0 0 2 ] \begin{bmatrix}2 &0\\ 0&2\\ \end{bmatrix} [2002]之后, i ^ \hat i i^变为原来两倍, j ^ \hat j j^也变为两倍,所以基向量构成的面积大小变为4,是原来的四倍,其行列式的值=4)
如果行列式计算的值为0的话,说明矩阵中的列向量线性相关,因为行列式变为0代表了面积/体积消失了。意味着原来的张成空间发生了降维,只有在矩阵的列向量线性相关时才会发生张成空间降维的现象。
若行列式为负则说明变换后的空间相对于原空间发生了翻转。
对角矩阵
M = [ 1 0 0 0 0 2 0 0 0 0 3 0 0 0 0 4 ] M=\begin{bmatrix}1 &0 &0& 0\\ 0&2&0&0\\ 0&0&3&0\\ 0&0&0&4 \end{bmatrix} M= 1000020000300004
像这样,对角元素非零,其余元素都为0的矩阵被我们称为对角矩阵,对角矩阵的行列式等于对角元素之积。
单位矩阵
单位矩阵我们通常用 E E E来表示,一个4×4的单位矩阵如下:
E = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] E=\begin{bmatrix}1 &0 &0& 0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{bmatrix} E= 1000010000100001
单位矩阵是一种特殊的对角矩阵,其对角元都为1。任何矩阵乘以单位矩阵结果都为它自身。(很简单,因为对每个向量的每个维度应用了乘以1的变换,就是没变)
即: E M = M E = M EM=ME=M EM=ME=M
转置矩阵
转置矩阵就是对矩阵进行翻转,行变列,列变行:
M i j T = M j i M^T_{ij} = M_{ji} MijT=Mji
[ 6 2 1 3 7 4 8 1 ] T = [ 6 7 2 4 1 2 3 1 ] \begin{bmatrix}6 &2 &1& 3\\ 7&4&8&1\end{bmatrix}^T = \begin{bmatrix}6 &7\\ 2&4\\ 1 &2\\ 3 &1\\ \end{bmatrix} [67241831]T= 62137421
性质:
- ( M T ) T = M (M^T)^T=M (MT)T=M,转了再转,等于没转
- ( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT
逆矩阵
像要求出逆矩阵,首先必须得是一个方阵
逆矩阵从数字意义上来讲,可以用于解方程组,例如:
2 x + 5 y + 3 z = − 3 4 x + 0 y + 8 z = 0 1 x + 3 y + 0 z = 2 2x+5y+3z=-3\newline 4x+0y+8z=0\newline 1x+3y+0z=2 2x+5y+3z=−34x+0y+8z=01x+3y+0z=2
如这个方程组,如果我们将其表示为线性代数则为:
[ 2 5 3 4 0 8 1 3 0 ] [ x y z ] = [ − 3 0 2 ] \begin{bmatrix}2&5 &3\\ 4&0&8\\ 1&3&0 \end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}=\begin{bmatrix}-3\\ 0\\ 2\end{bmatrix} 241503380 xyz = −302
我们将该式记为: A x = v Ax=v Ax=v
在上述式子就变成了对向量x应用线性变换A后得到最终向量v。那么解方程的问题就转换为求解该向量 [ x y z ] \begin{bmatrix}x\\ y\\ z\end{bmatrix} xyz
应用线性变换A后,我们可以从x变换到v,那么同样的也可以应用另一种线性变换从v变换到x,这个线性变换在几何上直观的来看就是A的逆变换。我们将这个变换记作 A − 1 A^{-1} A−1,也就是A的逆矩阵。
如果应用了线性变换 A A A之后,再应用线性变换 A − 1 A^{-1} A−1,其实相当于将向量变换过去,再变换回来,本质上和我们什么都没做一样,就相当于乘以了一个单位矩阵,因此有:
A A − 1 = A − 1 A = E AA^{-1}=A^{-1}A=E AA−1=A−1A=E
方程 A x = v Ax=v Ax=v就可以表示为 x = A − 1 v x=A^{-1}v x=A−1v
如果一个方阵的行列式=0,那么这个方阵就没有逆矩阵,我们将其称为“奇异矩阵”,很简单的原理,因为行列式等于0代表了张成空间的降维,我们可以将空间从高维降到低维,但是想要从低维升至高维还要找到唯一确定的原空间,抱歉,没有任何一个函数可以做到这点,因为函数是一对一的映射,而这样的逆变换注定有多种结果。
所以如果一个方阵的行列式不为0,则代表它存在逆矩阵。
性质:
- ( M − 1 ) − 1 = M (M^{-1})^{-1}=M (M−1)−1=M
- E − 1 = E E^{-1}=E E−1=E
- ( M T ) − 1 = ( M − 1 ) T (M^T)^{-1}=(M^{-1})^T (MT)−1=(M−1)T
- ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1,同样可以推广到多矩阵: ( A B C D ) − 1 = D − 1 C − 1 B − 1 A − 1 (ABCD)^{-1}=D^{-1}C^{-1}B^{-1}A^{-1} (ABCD)−1=D−1C−1B−1A−1
正交矩阵
如果一个方阵 M M M和它的转置矩阵 M T M^{T} MT的乘积是单位矩阵,也就是 M M T = M T M = E MM^T=M^TM=E MMT=MTM=E。则我们称该方阵M为正交矩阵。
如果该矩阵M还是可逆的,那么就有 M M T = M M − 1 = E MM^T=MM^{-1}=E MMT=MM−1=E,所以 M T = M − 1 M^T=M^{-1} MT=M−1
这个性质很重要,这样我们就不必求矩阵的逆,直接使用转置矩阵就得到矩阵的逆了。
一个矩阵想要是正交矩阵,那么必须满足以下性质:
- 方阵中的每个列向量和行向量的模长为1
- 所有列向量以及行向量都满足两两正交(内积为0)
模长为1代表该向量为单位向量(若模长不为1则最终结果一定是单位矩阵的倍数)。
而两两正交代表所有向量构成了正交基,这不就是我们之前学到的笛卡尔坐标系的定义吗?
若同时满足上述两种条件,则称基向量构成了标准正交基。