门控融合网络 (GFN) 和混合专家 (MoE)
门控融合网络 (GFN) 和混合专家 (MoE) 都是神经网络中使用的架构,特别是用于处理需要组合来自多个来源或模型的信息的复杂数据和任务。以下是每项的概述:
1. Gated Fusion Network (GFN):门控融合网络(GFN):
GFN 旨在通过学习门控机制来融合或合并来自不同模式或来源的信息。它由多个数据处理流组成,每个数据处理流都专注于特定方面或信息源。
门控机制控制每个流对最终预测或输出贡献的权重。
通过学习这些门函数,GFN 可以有效地结合不同的信息源。
门控融合网络旨在通过学习控制信息集成方式的门控机制来融合来自多个来源的信息。它包含处理不同类型数据的各种路径,门控机制决定每个路径对最终输出贡献多少权重。这种门控机制允许网络动态地强调或弱化特定信息源,从而实现更好的表示学习并捕获输入之间的复杂依赖关系。
1.1 代码举例
import torch
import torch.nn as nn
class GatedFusionNetwork(nn.Module):
def __init__(self, input_size1, input_size2, hidden_size):
super(GatedFusionNetwork, self).__init__()
self.pathway1 = nn.Linear(input_size1, hidden_size)
self.pathway2 = nn.Linear(input_size2, hidden_size)
self.gating = nn.Sequential(
nn.Linear(hidden_size * 2, hidden_size),
nn.Sigmoid()
)
self.output = nn.Linear(hidden_size, 1)
def forward(self, input1, input2):
out1 = torch.relu(self.pathway1(input1))
out2 = torch.relu(self.pathway2(input2))
fused = torch.cat((out1, out2), dim=1)
gate = self.gating(fused)
gated_output = gate * out1 + (1 - gate) * out2
output = self.output(gated_output)
return output
# Example Usage:
input_data1 = torch.randn(1, 10) # Fake input 1
input_data2 = torch.randn(1, 5) # Fake input 2
model = GatedFusionNetwork(10, 5, 20)
output = model(input_data1, input_data2)
print(output.item()) # Fake output
2. Mixture of Experts (MoE) Expert Network:专家混合 (MoE) 专家网络:
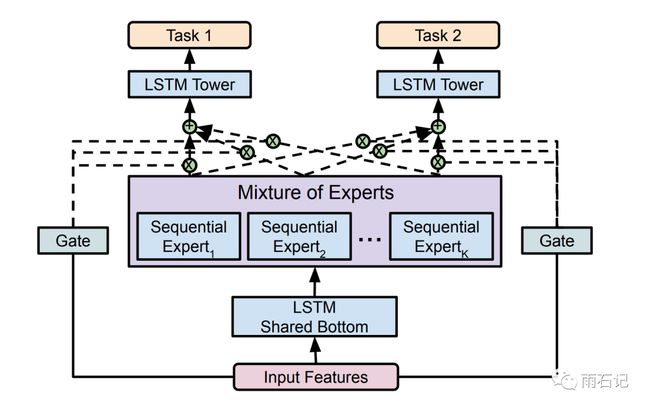
专家混合模型涉及多个称为专家的子网络,它们专门研究输入空间的不同部分。它由一个门控网络组成,用于确定哪个专家或专家组合最适合处理特定输入。每个专家都专注于数据的特定区域或方面,门控机制决定如何组合他们的输出以产生最终输出。
MoE 是一种神经网络架构,涉及多个协同工作的“专家”子网络(较小的神经网络),每个子网络专门研究输入空间的一个子集。这些专家做出单独的预测,门控网络决定每个专家的输出对最终预测的贡献程度。 MoE 可以通过允许不同的专家专门研究数据的不同区域或方面来处理数据中的复杂模式。
2.1 代码举例
class Expert(nn.Module):
def __init__(self, input_size, hidden_size):
super(Expert, self).__init__()
self.fc = nn.Linear(input_size, hidden_size)
self.output = nn.Linear(hidden_size, 1)
def forward(self, x):
out = torch.relu(self.fc(x))
return self.output(out)
class MixtureOfExperts(nn.Module):
def __init__(self, num_experts, input_size, hidden_size):
super(MixtureOfExperts, self).__init__()
self.experts = nn.ModuleList([Expert(input_size, hidden_size) for _ in range(num_experts)])
self.gating = nn.Sequential(
nn.Linear(input_size, num_experts),
nn.Softmax(dim=1)
)
def forward(self, x):
gates = self.gating(x)
expert_outs = [expert(x) for expert in self.experts]
weighted_outs = [gate * expert_out for gate, expert_out in zip(gates.unbind(1), expert_outs)]
output = torch.stack(weighted_outs, dim=2).sum(dim=2)
return output.squeeze()
# Example Usage:
input_data = torch.randn(1, 10) # Fake input
model = MixtureOfExperts(3, 10, 20)
output = model(input_data)
print(output.item()) # Fake output
2.2 gpt 中的相关
混合专家模型(Mixture of Experts, MoE)是一种用于解决大规模数据集上的复杂任务的神经网络模型。它可以自适应地组合多个专家网络来处理不同的数据子集,从而提高模型的泛化能力和性能。本文将对MoE模型的原理进行讲解,包括其数学公式和代码实现。
专家混合 (MoE) 是 LLM 中常用的一种技术,旨在提高其效率和准确性。这种方法的工作原理是将复杂的任务划分为更小、更易于管理的子任务,每个子任务都由专门的迷你模型或「专家」处理。
具体来说,「专家层」是较小的神经网络,经过训练在特定领域具有高技能,每个专家处理相同的输入,但处理方式与其特定的专业相一致;「门控网络」是 MoE 架构的决策者,能评估哪位专家最适合给定的输入数据。网络计算输入与每个专家之间的兼容性分数,然后使用这些分数来确定每个专家在任务中的参与程度。
我们都知道,OpenAI 团队一直对 GPT-4 的参数量和训练细节守口如瓶。早些时候,有人爆料 GPT-4 是采用了由 8 个专家模型组成的集成系统。后来又有传闻称,ChatGPT 也只是百亿参数级的模型(大概在 200 亿左右)。
传闻无从证明,但 Mistral 8x7B 可能提供了一种「非常接近 GPT-4」的开源选项。从模型元数据中可以看出,对于每个 token 的推理,Mistral 8x7B 仅使用 2 个专家。
MoE模型原理
2.1.1 基本结构
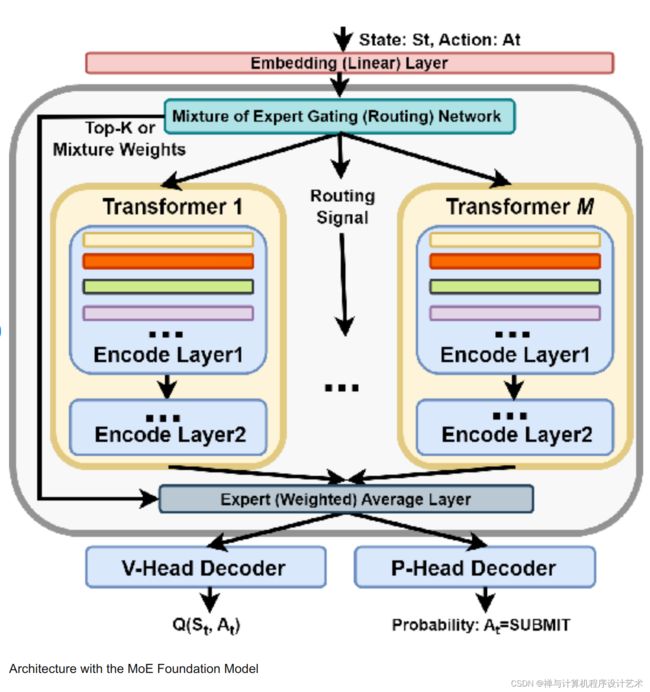
MoE模型由两部分组成:门控网络和专家网络。门控网络用于选择哪个专家网络处理输入数据,而每个专家网络负责处理相应的数据子集。
下图展示了一个有三个专家的两路数据并行MoE模型进行前向计算的方式.
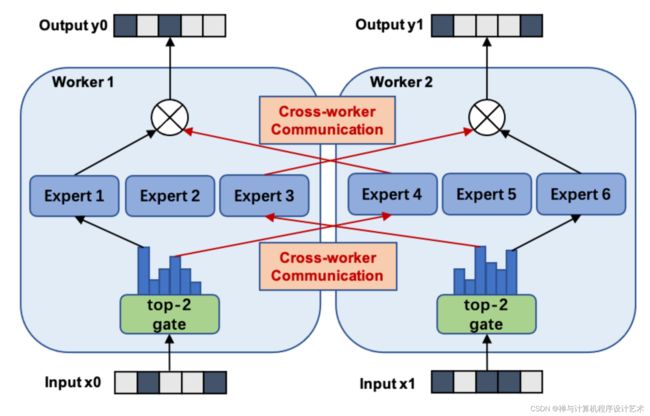
下图展示了一个有六个专家网络的模型被两路模型并行地训练.
注意专家1-3被放置在第一个计算单元上, 而专家4-6被放置在第二个计算单元上.
2.1.2 门控网络
门控网络用于选择哪个专家网络处理输入数据。它的输出结果是一个概率向量,表示每个专家网络被选择的概率。MoE模型中常用的门控网络是Softmax门控网络和Gating Tree门控网络。
2.1.3 Softmax门控网络
Softmax门控网络是一种基于Softmax函数的门控网络。
4. 代码实现
# Sparsely-Gated Mixture-of-Experts Layers.
# See "Outrageously Large Neural Networks"
# https://arxiv.org/abs/1701.06538
#
# Author: David Rau
#
# The code is based on the TensorFlow implementation:
# https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/utils/expert_utils.py
import torch
import torch.nn as nn
from torch.distributions.normal import Normal
import numpy as np
class SparseDispatcher(object):
"""Helper for implementing a mixture of experts.
The purpose of this class is to create input minibatches for the
experts and to combine the results of the experts to form a unified
output tensor.
There are two functions:
dispatch - take an input Tensor and create input Tensors for each expert.
combine - take output Tensors from each expert and form a combined output
Tensor. Outputs from different experts for the same batch element are
summed together, weighted by the provided "gates".
The class is initialized with a "gates" Tensor, which specifies which
batch elements go to which experts, and the weights to use when combining
the outputs. Batch element b is sent to expert e iff gates[b, e] != 0.
The inputs and outputs are all two-dimensional [batch, depth].
Caller is responsible for collapsing additional dimensions prior to
calling this class and reshaping the output to the original shape.
See common_layers.reshape_like().
Example use:
gates: a float32 `Tensor` with shape `[batch_size, num_experts]`
inputs: a float32 `Tensor` with shape `[batch_size, input_size]`
experts: a list of length `num_experts` containing sub-networks.
dispatcher = SparseDispatcher(num_experts, gates)
expert_inputs = dispatcher.dispatch(inputs)
expert_outputs = [experts[i](expert_inputs[i]) for i in range(num_experts)]
outputs = dispatcher.combine(expert_outputs)
The preceding code sets the output for a particular example b to:
output[b] = Sum_i(gates[b, i] * experts[i](inputs[b]))
This class takes advantage of sparsity in the gate matrix by including in the
`Tensor`s for expert i only the batch elements for which `gates[b, i] > 0`.
"""
def __init__(self, num_experts, gates):
"""Create a SparseDispatcher."""
self._gates = gates
self._num_experts = num_experts
# sort experts
sorted_experts, index_sorted_experts = torch.nonzero(gates).sort(0)
# drop indices
_, self._expert_index = sorted_experts.split(1, dim=1)
# get according batch index for each expert
self._batch_index = torch.nonzero(gates)[index_sorted_experts[:, 1], 0]
# calculate num samples that each expert gets
self._part_sizes = (gates > 0).sum(0).tolist()
# expand gates to match with self._batch_index
gates_exp = gates[self._batch_index.flatten()]
self._nonzero_gates = torch.gather(gates_exp, 1, self._expert_index)
def dispatch(self, inp):
"""Create one input Tensor for each expert.
The `Tensor` for a expert `i` contains the slices of `inp` corresponding
to the batch elements `b` where `gates[b, i] > 0`.
Args:
inp: a `Tensor` of shape "[batch_size, ]`
Returns:
a list of `num_experts` `Tensor`s with shapes
`[expert_batch_size_i, ]`.
"""
# assigns samples to experts whose gate is nonzero
# expand according to batch index so we can just split by _part_sizes
inp_exp = inp[self._batch_index].squeeze(1)
return torch.split(inp_exp, self._part_sizes, dim=0)
def combine(self, expert_out, multiply_by_gates=True):
"""Sum together the expert output, weighted by the gates.
The slice corresponding to a particular batch element `b` is computed
as the sum over all experts `i` of the expert output, weighted by the
corresponding gate values. If `multiply_by_gates` is set to False, the
gate values are ignored.
Args:
expert_out: a list of `num_experts` `Tensor`s, each with shape
`[expert_batch_size_i, ]`.
multiply_by_gates: a boolean
Returns:
a `Tensor` with shape `[batch_size, ]`.
"""
# apply exp to expert outputs, so we are not longer in log space
stitched = torch.cat(expert_out, 0).exp()
if multiply_by_gates:
stitched = stitched.mul(self._nonzero_gates)
zeros = torch.zeros(self._gates.size(0), expert_out[-1].size(1), requires_grad=True, device=stitched.device)
# combine samples that have been processed by the same k experts
combined = zeros.index_add(0, self._batch_index, stitched.float())
# add eps to all zero values in order to avoid nans when going back to log space
combined[combined == 0] = np.finfo(float).eps
# back to log space
return combined.log()
def expert_to_gates(self):
"""Gate values corresponding to the examples in the per-expert `Tensor`s.
Returns:
a list of `num_experts` one-dimensional `Tensor`s with type `tf.float32`
and shapes `[expert_batch_size_i]`
"""
# split nonzero gates for each expert
return torch.split(self._nonzero_gates, self._part_sizes, dim=0)
class MLP(nn.Module):
def __init__(self, input_size, output_size, hidden_size):
super(MLP, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, output_size)
self.relu = nn.ReLU()
self.soft = nn.Softmax(1)
def forward(self, x):
out = self.fc1(x)
out = self.relu(out)
out = self.fc2(out)
out = self.soft(out)
return out
class MoE(nn.Module):
"""Call a Sparsely gated mixture of experts layer with 1-layer Feed-Forward networks as experts.
Args:
input_size: integer - size of the input
output_size: integer - size of the input
num_experts: an integer - number of experts
hidden_size: an integer - hidden size of the experts
noisy_gating: a boolean
k: an integer - how many experts to use for each batch element
"""
def __init__(self, input_size, output_size, num_experts, hidden_size, noisy_gating=True, k=4):
super(MoE, self).__init__()
self.noisy_gating = noisy_gating
self.num_experts = num_experts
self.output_size = output_size
self.input_size = input_size
self.hidden_size = hidden_size
self.k = k
# instantiate experts
self.experts = nn.ModuleList([MLP(self.input_size, self.output_size, self.hidden_size) for i in range(self.num_experts)])
self.w_gate = nn.Parameter(torch.zeros(input_size, num_experts), requires_grad=True)
self.w_noise = nn.Parameter(torch.zeros(input_size, num_experts), requires_grad=True)
self.softplus = nn.Softplus()
self.softmax = nn.Softmax(1)
self.register_buffer("mean", torch.tensor([0.0]))
self.register_buffer("std", torch.tensor([1.0]))
assert(self.k <= self.num_experts)
def cv_squared(self, x):
"""The squared coefficient of variation of a sample.
Useful as a loss to encourage a positive distribution to be more uniform.
Epsilons added for numerical stability.
Returns 0 for an empty Tensor.
Args:
x: a `Tensor`.
Returns:
a `Scalar`.
"""
eps = 1e-10
# if only num_experts = 1
if x.shape[0] == 1:
return torch.tensor([0], device=x.device, dtype=x.dtype)
return x.float().var() / (x.float().mean()**2 + eps)
def _gates_to_load(self, gates):
"""Compute the true load per expert, given the gates.
The load is the number of examples for which the corresponding gate is >0.
Args:
gates: a `Tensor` of shape [batch_size, n]
Returns:
a float32 `Tensor` of shape [n]
"""
return (gates > 0).sum(0)
def _prob_in_top_k(self, clean_values, noisy_values, noise_stddev, noisy_top_values):
"""Helper function to NoisyTopKGating.
Computes the probability that value is in top k, given different random noise.
This gives us a way of backpropagating from a loss that balances the number
of times each expert is in the top k experts per example.
In the case of no noise, pass in None for noise_stddev, and the result will
not be differentiable.
Args:
clean_values: a `Tensor` of shape [batch, n].
noisy_values: a `Tensor` of shape [batch, n]. Equal to clean values plus
normally distributed noise with standard deviation noise_stddev.
noise_stddev: a `Tensor` of shape [batch, n], or None
noisy_top_values: a `Tensor` of shape [batch, m].
"values" Output of tf.top_k(noisy_top_values, m). m >= k+1
Returns:
a `Tensor` of shape [batch, n].
"""
batch = clean_values.size(0)
m = noisy_top_values.size(1)
top_values_flat = noisy_top_values.flatten()
threshold_positions_if_in = torch.arange(batch, device=clean_values.device) * m + self.k
threshold_if_in = torch.unsqueeze(torch.gather(top_values_flat, 0, threshold_positions_if_in), 1)
is_in = torch.gt(noisy_values, threshold_if_in)
threshold_positions_if_out = threshold_positions_if_in - 1
threshold_if_out = torch.unsqueeze(torch.gather(top_values_flat, 0, threshold_positions_if_out), 1)
# is each value currently in the top k.
normal = Normal(self.mean, self.std)
prob_if_in = normal.cdf((clean_values - threshold_if_in)/noise_stddev)
prob_if_out = normal.cdf((clean_values - threshold_if_out)/noise_stddev)
prob = torch.where(is_in, prob_if_in, prob_if_out)
return prob
def noisy_top_k_gating(self, x, train, noise_epsilon=1e-2):
"""Noisy top-k gating.
See paper: https://arxiv.org/abs/1701.06538.
Args:
x: input Tensor with shape [batch_size, input_size]
train: a boolean - we only add noise at training time.
noise_epsilon: a float
Returns:
gates: a Tensor with shape [batch_size, num_experts]
load: a Tensor with shape [num_experts]
"""
clean_logits = x @ self.w_gate
if self.noisy_gating and train:
raw_noise_stddev = x @ self.w_noise
noise_stddev = ((self.softplus(raw_noise_stddev) + noise_epsilon))
noisy_logits = clean_logits + (torch.randn_like(clean_logits) * noise_stddev)
logits = noisy_logits
else:
logits = clean_logits
# calculate topk + 1 that will be needed for the noisy gates
top_logits, top_indices = logits.topk(min(self.k + 1, self.num_experts), dim=1)
top_k_logits = top_logits[:, :self.k]
top_k_indices = top_indices[:, :self.k]
top_k_gates = self.softmax(top_k_logits)
zeros = torch.zeros_like(logits, requires_grad=True)
gates = zeros.scatter(1, top_k_indices, top_k_gates)
if self.noisy_gating and self.k < self.num_experts and train:
load = (self._prob_in_top_k(clean_logits, noisy_logits, noise_stddev, top_logits)).sum(0)
else:
load = self._gates_to_load(gates)
return gates, load
def forward(self, x, loss_coef=1e-2):
"""Args:
x: tensor shape [batch_size, input_size]
train: a boolean scalar.
loss_coef: a scalar - multiplier on load-balancing losses
Returns:
y: a tensor with shape [batch_size, output_size].
extra_training_loss: a scalar. This should be added into the overall
training loss of the model. The backpropagation of this loss
encourages all experts to be approximately equally used across a batch.
"""
gates, load = self.noisy_top_k_gating(x, self.training)
# calculate importance loss
importance = gates.sum(0)
#
loss = self.cv_squared(importance) + self.cv_squared(load)
loss *= loss_coef
dispatcher = SparseDispatcher(self.num_experts, gates)
expert_inputs = dispatcher.dispatch(x)
gates = dispatcher.expert_to_gates()
expert_outputs = [self.experts[i](expert_inputs[i]) for i in range(self.num_experts)]
y = dispatcher.combine(expert_outputs)
return y, loss
https://github.com/davidmrau/mixture-of-experts
MoSE
References
GitHub - XueFuzhao/awesome-mixture-of-experts: A collection of AWESOME things about mixture-of-experts
3. 差异和联系:
-
GFN 专注于使用门控机制融合来自不同来源或模式的信息,门控机制:GFN 主要关注集成信息的门控机制;而 MoE 使用门控将输入路由到不同的专家, MoE 专注于创建一个专家网络,共同为最终预测做出贡献。
-
MoE 明确使用多个专门的子网络(专家),而 GFN 经常集成来自不同路径的信息,而没有明确的专门模块。
-
架构差异:GFN 将多个数据流与门控机制相结合,而 MoE 由多个专家网络组成,并通过门控机制来衡量其贡献。
-
信息处理:GFN强调多源信息的动态融合,而MoE则注重专家的专门处理。
Application: Both architectures aim to handle complex information integration but may be suited to different types of problems or data structures. GFN may be more versatile when integrating diverse information sources, while MoE might excel when the problem benefits from specialized experts.
reference
https://blog.csdn.net/m0_64768308/article/details/133963803#t3