02局部可观测随机博弈过程
文章目录
- 前言
-
- 部分可观测的随机博弈过程(POSG)
-
- 局部观测
- 局部观测函数
- 信念状态
- 信念状态卷积
前言
局部可观测随机博弈过程
部分可观测的随机博弈过程(POSG)
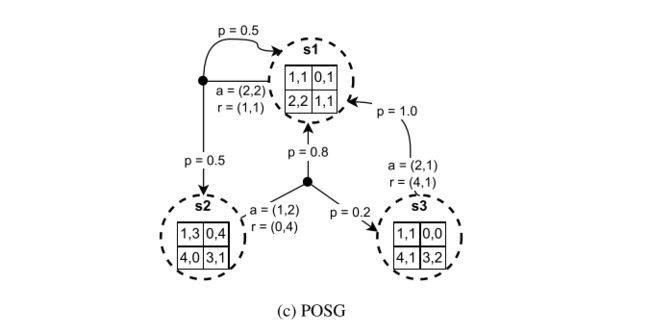
POSG过程中,每个智能体只能观测部分环境状态与其他智能体的采取的动作信息,局部可观察状态转移概率为 Pr ( s t , o t ∣ s t − 1 , a t − 1 ) \Pr(s^{t},o^{t}\mid s^{t-1},a^{t-1}) Pr(st,ot∣st−1,at−1),其中 o t = ( o 1 t , . . . , o n t ) o^{t}=(o_{1}^{t},...,o_{n}^{t}) ot=(o1t,...,ont)表示智能体t时刻的联合观测序列,观测结果只依赖于新的环境状态与生成新状态的联合动作,因此需要为每个智能体定义单独的观察函数,得到POSG的定义:

在初始状态分布下,在t时刻,每个智能体根据观测函数 O i ( o i t ∣ a t − 1 , s t ) \mathcal{O}_i(o_i^t|a^{t-1},s^t) Oi(oit∣at−1,st)得到观测信息 o i t ∈ O i o_i^t\in O_i oit∈Oi,根据策略采取动作,得到联合动作,在这里的策略函数 π i ( a i t ∣ h i t ) \pi_{i}(a_{i}^{t}|h_{i}^{t}) πi(ait∣hit)是根据每个智能体的历史观测序列 h i t = ( o i 0 , . . . , o i t ) h_{i}^{t}=(o_{i}^0,...,o_{i}^{t}) hit=(oi0,...,oit)得到的。得到联合动作后,根据 T ( s t + 1 ∣ s t , a t ) \mathcal{T}(s^{t+1}\mid s^{t},a^{t}) T(st+1∣st,at)转移到下一个状态,每个智能体得到奖励 r i t = R i ( s t , a t , s t + 1 ) r_{i}^{t}={\mathcal R}_{i}(s^{t},a^{t},s^{t+1}) rit=Ri(st,at,st+1),重复上述步骤,直到到达终止状态。
局部观测
其他智能体的动作不可观测:每个智能体只能观测到环境与自己的动作、有限的视野:每个智能体观测到的环境与联合动作的一部分,是由于视野受限造成的。

局部观测函数
局部观测函数能够建模观测中的不确定性:将多个可能的观测结果赋予非零的概率。够建模范围受限或不可信智能体之间的通信:在范围受限的情况下,将交流信息形式化为多值向量,其并不会修改环境的状态,但能够被其他的智能的观测结果中接受;不可靠的通信能够形式为为特定的概率表达信息的丢失。
信念状态
在POSG环境中,智能体只能观测到当前环境的部分信息,因此并不能够找到最优动作,然而智能体能够通过历史的观测序列推断出目前环境的状态分布从而选择最优的动作,因此定义信念状态: b i t + 1 ( s ′ ) = η ∑ s ∈ S b i t ( s ) T ( s ′ ∣ s , a i t ) O i ( o i t + 1 ∣ a i t , s ′ ) b_i^{t+1}(s^{\prime})=\eta\sum_{s\in S}b_i^t(s)\mathcal{T}(s^{\prime}|s,a_i^t)\mathcal{O}_i(o_i^{t+1}|a_i^t,s^{\prime}) bit+1(s′)=η∑s∈Sbit(s)T(s′∣s,ait)Oi(oit+1∣ait,s′),表示t时刻时状态的概率分布。
信念状态是通过收集过去的观测信息得到的,因此能够准确的用于选择最优动作、做出决策。
信念状态卷积
信念状态的更新过程依赖于过去的观测,因此也称为信念状态的卷积。然而随着智能体的增加,信念状态导致复杂度呈指数形式增长,同时智能体并不能观测到其他智能体的动作以及观测结果等,这些都是在更新信念状态时必需的信息,因此信念状态的引入导致问题更加复杂。
在MARL中,一般使用RNN生成观测序列,利用观测序列编码环境信息,输入到后面的值或策略网络中。