代码随想录刷题笔记(DAY 10)
今日总结:快要期末考试了,现在在疯狂速成,今天稍微缓和了一点,应该能保证继续每天刷题,欠下的那些寒假补上。
Day 10
01. 用栈实现队列(No. 232)
题目链接
代码随想录题解
1.1 题目
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false
说明:
- 你 只能 使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。 - 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
示例 1:
输入:
[“MyQueue”, “push”, “push”, “peek”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 1, 1, false]解释:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false
提示:
1 <= x <= 9- 最多调用
100次push、pop、peek和empty - 假设所有操作都是有效的 (例如,一个空的队列不会调用
pop或者peek操作)
1.2 笔记
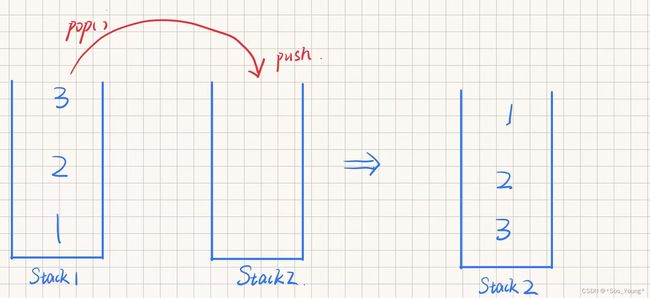
非常经典的题目,考察了对这两个数据结构的理解。栈实现了“先进后出”而队列则是“先进先出”,所以如果我们想要借助栈来实现队列的话,很容易就想到我们在输出的时候将栈中的数据反转即可,那反转如何实现呢?
这就需要用到两个栈:
即将 Stack1 视作一个 中转站,当我们需要输出的时候,就将 Stack1 中的元素 pop() 到 Stack2 中,然后从 Stack2 中取元素。
注意 push() 的时候要判断 Stack2 是否为空,如果不为空就会出现顺序问题,因为此时的 Stack2 中即将弹出的第一个元素是我们构造的队列的第一个元素,如果我们在 Stack2 还未空的时候就 push() 新元素进来,就打破了确定的顺序。
1.3 代码
class MyQueue {
Stack<Integer> s1;
Stack<Integer> s2;
public MyQueue() {
// 初始化
s1 = new Stack<>();
s2 = new Stack<>();
}
public void push(int x) {
// 每次放入新元素的时候都暂存到 s1
s1.push(x);
}
public int pop() {
if (s2.empty()) {
while (!s1.empty()) {
s2.push(s1.pop());
}
}
return s2.pop();
}
public int peek() {
// 判断 s2 是否为空
if (s2.empty()) {
while (!s1.empty()) {
s2.push(s1.pop());
}
}
return s2.peek();
}
public boolean empty() {
return s1.empty() && s2.empty();
}
}
02. 用队列实现栈
题目链接
代码随想录题解
2.1 题目
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
注意:
- 你只能使用队列的基本操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。 - 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入:
[“MyStack”, “push”, “push”, “top”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 2, 2, false]解释:
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False
提示:
1 <= x <= 9- 最多调用
100次push、pop、top和empty - 每次调用
pop和top都保证栈不为空
2.2 笔记
有了上面那道题的经验,很多朋友拿到这道题就想着想上面那道题一样倒过来就行了,那怎样倒过来呢?
简单,在创建一个队列然后从第一个队列推入就行了。
但是提交发现题目还是错了,这是为什么呢?
队列是先进先出的数据结构,我们把一个队列一个个取出放入另一个队列,顺序是不会改变的,就像正数乘以一个整数还是整数,栈能够倒置原因就是它是先进后出,负数乘以负数结果就是正数,这样类比起来就比较好理解。
这道题目可以使用一个队列来实现,队列的队尾元素是栈的栈顶元素:
那如果想要删除这个队尾的元素,我们可以从队头开始遍历,然后将队头的元素依次放到队尾,直到最开始的队尾元素(栈顶)是队列的队头的时候停止,也就是需要遍历 size - 1 次,这时候将队头元素弹出得到的就是需要的元素了。
那如何获取队尾元素呢?
我们可以按照上面的方法循环 size- 1 然后得到队头的元素但不删除。但其实我们可以设置一个变量 lastNum 当我们需要队尾元素的时候就直接将这个返回。
如果没有删除元素的话那这个 lastNum 的值就很好确定,我们每次 add() 添加新元素的时候就将 lastNum 重置为这个值即可,那如果执行了删除的话,这时候原本的倒数第二个元素就成了新的 lastNum 我们只需要在遍历到倒数第二个元素的时候将其赋值即可。
2.3 代码
class MyStack {
Queue<Integer> q1;
int lastNum; // 记录最后一个元素的值
public MyStack() {
q1 = new ArrayDeque<>();
}
public void push(int x) {
q1.add(x);
lastNum = x;
}
public int pop() {
int size = q1.size();
size = size - 1;
while (size-- > 0) {
int temp = q1.remove(); // 记录此时弹出的元素
q1.add(temp);
// 当循环结束的时候就将其赋值成倒数第二个元素了,其实等价于 if (size == 0) {lastNum = temp; }
lastNum = temp;
}
return q1.remove();
}
public int top() {
return lastNum;
}
public boolean empty() {
return q1.isEmpty();
}
}