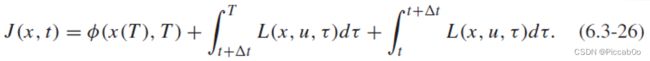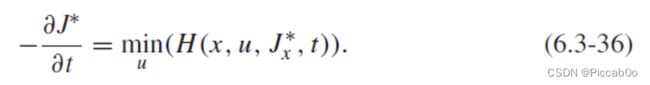【最优控制笔记】——3动态规划之连续系统2
动态规划
6.3连续系统的动态规划
说明:
本节主要阐述连续系统动态规划的第二种求解思路,其系统及性能指标形式为:


目的是:找到区间 [ t 0 , T ] [t_0,T] [t0,T]上的连续控制量 u ∗ ( t ) u^*(t) u∗(t)使性能指标 J J J最小,且使状态 x ( t 0 ) x(t_0) x(t0)到达满足下式的终端状态:
6.3.2 动态规划与连续控制
思路:
对于系统的性能指标(6.3-24)而言,利用 Δ t \Delta t Δt,其可以改写成:
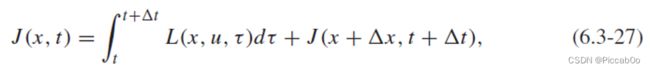
根据最优性原理, J ∗ ( x , t ) J^*(x,t) J∗(x,t)一定需要 J ( x , t ) J(x,t) J(x,t)从 t + Δ t t+\Delta t t+Δt到 T T T都最优。
如果 [ t + Δ t , T ] [t+\Delta t,T] [t+Δt,T]上的 x + Δ x x+\Delta x x+Δx和 J ∗ ( x + Δ x , t + Δ t ) J^*(x+\Delta x,t+\Delta t) J∗(x+Δx,t+Δt)我们都已知,则只需要选择控制量 u ( t ) u(t) u(t),因此最优控制下的性能指标可写作:
解决:
上式求解困难,因此还需要进一步对式(6.3-29)进行操作——进行 ( x , t ) (x,t) (x,t)处的一阶泰勒展开:
(这里,其实可以发现连续系统的Bellman原理其实只是一种一阶泰勒展开形式)
由(6.3-23)可得:

将偏微分简写成 J t ∗ J^*_t Jt∗和 J x ∗ J^*_x Jx∗的形式,有:

由于 Δ t \Delta t Δt趋近于0,故两边可消,有:
这个偏微分方程被称为Hamilton-Jacobi-Bellman (HJB) equation。
结合Hamilton函数可以发现,其只是将 λ \lambda λ换成了 ∂ J ∗ ∂ x \frac{\partial J^*}{\partial x} ∂x∂J∗,如果假设Hamilton函数为:

则HJB方程又可写作:
从时间 T T T向后推,其可以解决。其种,边界条件可由式(6.3-24)
在 t 0 = T t_0=T t0=T求得:
数学表达:
6.3.3 例1
解:
Hamliton函数为:
H ( x ( t ) , u ( t ) , V x ) = 1 4 u 2 ( t ) + V x ∗ ( x ( t ) + u ( t ) ) H(x(t),u(t),V_x)=\frac{1}{4}u^2(t)+V_x*(x(t)+u(t)) H(x(t),u(t),Vx)=41u2(t)+Vx∗(x(t)+u(t))
HJB方程为:
− V t = m i n [ H ( x ( t ) , u ( t ) , V x T ( x ( t ) , t ) , t ) ] - V_t =min[H(x(t),u(t),V_x^T(x(t),t),t)] −Vt=min[H(x(t),u(t),VxT(x(t),t),t)]
则有:
∂ H ∂ u = 1 2 u ( t ) + V x ( x ( t ) , t ) \frac{\partial H}{\partial u}=\frac{1}{2}u(t)+V_x(x(t),t) ∂u∂H=21u(t)+Vx(x(t),t)
∂ 2 H ∂ u 2 = 1 2 \frac{\partial ^2H}{\partial u^2}=\frac{1}{2} ∂u2∂2H=21
因此有最优控制量:
u ∗ ( t ) = − 2 V x ( x ( t ) , t ) u^*(t)=-2V_x(x(t),t) u∗(t)=−2Vx(x(t),t)
这里HJB方程可以写作:
− V t = 1 4 ( − 2 V x ) 2 + V x ( x ( t ) − 2 V x ) -V_t=\frac{1}{4}(-2V_x)^2+V_x(x(t)-2V_x) −Vt=41(−2Vx)2+Vx(x(t)−2Vx)
整理得:
0 = V t + V x x ( t ) − V x 2 0=V_t+V_xx(t)-V_x^2 0=Vt+Vxx(t)−Vx2
可以采用假定二次型的方法求解 V V V,进而求出 u ∗ ( t ) u^*(t) u∗(t),设:
V ( x ( t ) , t ) = 1 2 K ( t ) x 2 ( t ) V(x(t),t)=\frac{1}{2}K(t)x^2(t) V(x(t),t)=21K(t)x2(t)
V x = K ( t ) x ( t ) V_x=K(t)x(t) Vx=K(t)x(t)
V t = 1 2 K ˙ ( t ) x 2 ( t ) V_t=\frac{1}{2}\dot K(t)x^2(t) Vt=21K˙(t)x2(t)
因此代入上式有:
0 = 1 2 K ˙ ( t ) − K 2 ( t ) + K ( t ) 0=\frac{1}{2}\dot K(t)-K^2(t)+K(t) 0=21K˙(t)−K2(t)+K(t)
由边界条件:
V ( x ( t f ) , t f ) = 1 4 x 2 ( t f ) = 1 2 K ( t ) x 2 ( t f ) V(x(t_f),t_f)=\frac{1}{4}x^2(t_f)=\frac{1}{2}K(t)x^2(t_f) V(x(tf),tf)=41x2(tf)=21K(t)x2(tf)
得:
K ( t f ) = 1 2 K(t_f)=\frac{1}{2} K(tf)=21
因此,微分方程可利用分离变量法求解:
K ( t ) = 1 1 + e 2 ( t f − t ) K(t)=\frac{1}{1+e^{2(t_f-t)}} K(t)=1+e2(tf−t)1
6.3.4 例2
离控制目标越远,控制量变化uk越小;反之,变化越剧烈。
例题最小燃料问题的性能指标设置有误,不开车最好,J=0,所以改进加入终端约束
6.3.5 例3(值函数不可微的情况)
P a g e 40 − P a g e 44 Page_{40}-Page_{44} Page40−Page44