Perfect Sequence PTA
目录
题目简介
Input Specification:
Output Specification:
Sample Input:
Sample Output:
大意介绍
解题思路
代码实现
冒泡排序
快速排序
堆排序
AC_堆排序
题目简介
Given a sequence of positive integers and another positive integer p. The sequence is said to be a "perfect sequence" if M≤m×p where M and m are the maximum and minimum numbers in the sequence, respectively.
Now given a sequence and a parameter p, you are supposed to find from the sequence as many numbers as possible to form a perfect subsequence.
Input Specification:
Each input file contains one test case. For each case, the first line contains two positive integers N and p, where N (≤105) is the number of integers in the sequence, and p (≤109) is the parameter. In the second line there are N positive integers, each is no greater than 109.
Output Specification:
For each test case, print in one line the maximum number of integers that can be chosen to form a perfect subsequence.
Sample Input:
10 8
2 3 20 4 5 1 6 7 8 9Sample Output:
8大意介绍
第一行第一个数N(<=10^5),是第二行序列元素的个数;第二个数p(<=10^9),一个参数。输出是满足M<=m*p的元素个数,其中M是序列的最大值,m是序列中任意一个元素,p就是第一行第二个数。
解题思路
将序列从小到大排列,最大值和完美子序列元素的个数就出来了,满足M<=m*p的元素也从小到大排列在序列的右边。所以关键还是排列算法。//我理解的思路有问题,中间是出错的过程,正确结果直接看最下面AC的代码。
代码实现
冒泡排序
#include
#include
void sort(int *a,int n)//void删掉也没影响。不知道为什么
{
int change;int t;//c语言标准库里没有bool类型,要用要加上有bool函数的库,或者自己定义
for(int i=n-1,change=1;i>=1&&change;--i)//改进的冒泡算法
{
change=0;
for(int j=0;ja[j+1])//一趟结束后若已经a[j]<=a[j+1],就停止循环,可以减少趟数
{
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
change=1;
}
}
}
}
int main()
{
int n,p,i;
scanf("%d%d",&n,&p);
int a[n];
for(i=0;ia[i]*p)//统计不满足M<=m*p的元素个数
{i++;}
printf("%d\n",n-i);
} 有关bool(布尔)类型在C语言中的应用_bool在c语言中的用法-CSDN博客
中间曾出现过段错误,原因就在于标准库中没有bool类型。但改过来之后还是不过。
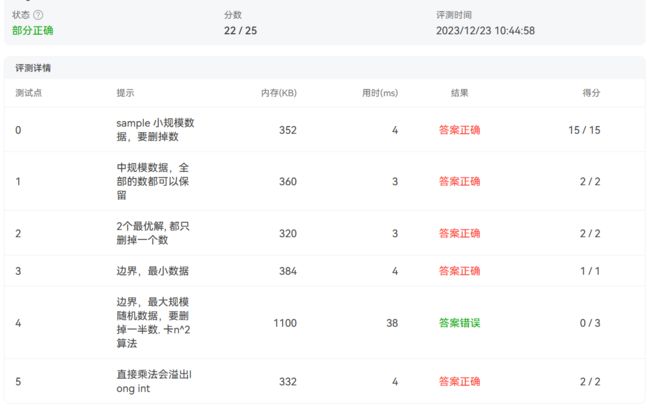
第4点明明的写着,卡n^2算法。所以换算法吧。
快速排序
#include
#include
void sort(long int *a,int low,int high)
{
int p;//枢纽
if(low < high)
{
p = Partition(a,low,high);
sort(a,low,p-1);
sort(a,p+1,high);
}
}
int Partition(long int *a,int low,int high)
{
int p;
p=a[0]=a[low];
while(low=p)
--high;
a[low]=a[high];
while(lowa[i]*p)//要改为long int 类型,防止乘法溢出
{i++;}//(乘法是有一个long int结果就是long int)
printf("%d\n",n-i+1);
} 中间检查出第五点的错误,并将数组由int类型改为long int类型。但第四点还没过,不过不是运行超时,而是答案错误。难道快速排序在大规模数据下会出错吗?留下一个悬念。
堆排序
代码,借鉴(可以说是全搬)自这篇文章
堆排序详细图解(通俗易懂)-CSDN博客
#include
#include
void HeapAdjust(long int* arr,int start,int end)
{
int tmp=arr[start];
for(int i=2*start+1;i<=end;i=i*2+1)
{
if(itmp)
{
arr[start]=arr[i];
start=i;
}
else
break;
}
arr[start]=tmp;//start已被修改为i。
}
void HeapSort(long int* arr,int len)
{
for(int i=(len-1-1)/2;i>=0;i--)
HeapAdjust(arr,i,len-1);
int tmp;
for(int i=0;ia[i]*p)
{i++;}
printf("%d\n",n-i);
}
人麻了,这是为什么啊?
上述排序算法都没有错误,所以我猜测是我的主函数出了问题,一开始检查没加return 0;可加上还是出错。于是我查看其他博主的博客,看他们是怎么输出最终结果的。
感谢这位博主的堆排序代码,让我更好的比对。
【C++】PTA Perfect Sequence 代码+过程_a - best sequencec++-CSDN博客
修改前与修改后比对
i=0;//修改前
while(a[n-1]>a[i]*p)
{i++;}
printf("%d\n",n-i);
int m=0;//修改后
for(i=0;i虽然不知道为什么我的原来的输出会在大规模数据下有问题,我猜测可能是大规模数据并不能完全升序排列,但可以保证最大的排在最后。我觉得,都不用那么麻烦,直接找出最大值就行了。
当我前面没说,原来不是排序的问题,而是完美子序列不是在最右边!!!
例子:7 10
1 1 1 1 1 1 100
若按我的想法,完美子序列的个数为1,因为其他的数都不满足100<=m*10,但这个序列的完美子序列是1 1 1 1 1 1,这个子序列的最小值为1,最大值为1.完全满足1<=1*10.
AC_堆排序
#include
#include
void HeapAdjust(long int* arr,int start,int end)
{
int tmp=arr[start];
for(int i=2*start+1;i<=end;i=i*2+1)
{
if(itmp)
{
arr[start]=arr[i];
start=i;
}
else
break;
}
arr[start]=tmp;//start已被修改为i。
}
void HeapSort(long int* arr,int len)
{
for(int i=(len-1-1)/2;i>=0;i--)
HeapAdjust(arr,i,len-1);
int tmp;
for(int i=0;i 当然,前面的排序算法都没有错,大家可以随意组合。