二叉查找树及C++模板实现

何为二叉查找树？

二叉查找树也称为二叉搜索树或二叉排序树。二叉排序树的节点包含键值key。二叉排序树或者是一棵空树，否则要求：

1.若它的左子树不为空，那么左子树上所有节点的key都小于根节点的key
2.若它的右子树不为空，那么右子树上所有节点的key都大于根节点的key
3.它的左右子树也分别为二叉排序树

从定义得，二叉查找树中没有重复key值的节点。

二叉查找树的构建

节点结构

template <typename T>
struct BSNode
{
    //初始化　只赋予权值
    BSNode(T t):value(t),lchild(NULL),rchild(NULL) {}
    //BSNode() = default;

    T value;            //节点的值
    BSNode* lchild;  //左孩子
    BSNode* rchild;  //右孩子
    BSNode* parent;  //节点的双亲
};

二叉查找树的抽象数据结构

template T>
class BSTree
{
public:
    //初始化为空树
    BSTree():root(NULL){}
//外部接口
    void preOrder();    //前序遍历 
    void inOrder();     //中序遍历
    void postOrder();   //后序遍历

    BSNode<T>* search_recursion(T key); //递归查找指定节点
    BSNode<T>* search__iterator(T key); //迭代查找指定节点

    T search_maxnum();      //查找最大元素
    T search_minnum();      //查找最小元素

    void insert(T key);     //插入指定结点
    void remove(T key);     //删除指定结点
    void destory();         //销毁二叉树
    void print();           //打印二叉树

private:
    BSNode<T>* root;        //根节点
//内部接口
    void preOrder(BSNode<T>* pnode);  
    void inOrder(BSNode<T>* pnode);
    void postOrder(BSNode<T>* pnode);

    BSNode<T>* search(BSNode<T>* & p,T key);

    void remove(BSNode<T>* pnode,T key);

    T search_maxnum(BSNode<T>* pnode);      
    T search_minnum(BSNode<T>* pnode);      

    void destory(BSNode<T>* &pnode);

};

具体实现

1. 插入节点

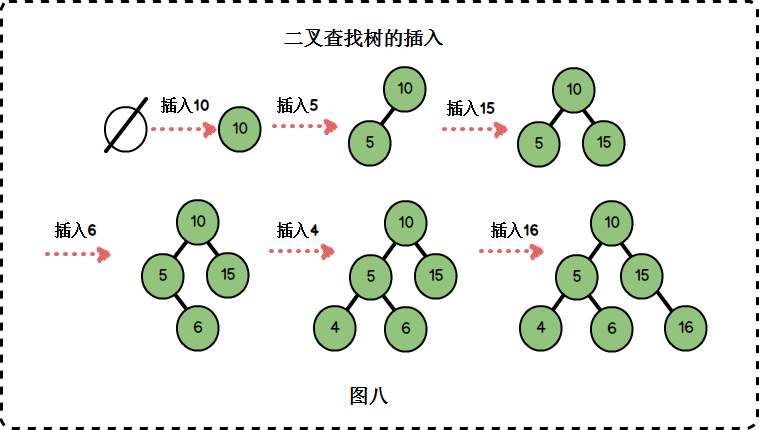
假设我们要为数组 a[] = {10 ， 5 ， 15 ， 6 ， 4 ， 16 }构建一个二叉查找树，我们按顺序逐个插入元素。

插入过程：

1. 如果是空树，则创建一个新节点，新节点作为根，因此以元素10构建的节点为该二叉查找树的根。
2. 插入5，5比10小，与10的左孩子节点进行比较，10的左孩子节点为空，进行插入。
3. 插入15，15比10大，与10的右孩子节点进行比较，10的右孩子节点为空，进行插入。
4. 插入6，6比10小，与10的左孩子节点5比较；6比5大，与5的右孩子节点进行比较，5的右孩子为空，进行插入。
   5.插入4，4比10小，与10的左孩子节点5比较；4比5小，与5的左孩子节点进行比较，5的左孩子为空，进行插入。
   6.插入16，16比10大，与10的右孩子节点15比较；16比15大，与15的右孩子节点进行比较，15的右孩子为空，进行插入。

从这个过程我们可以总结出插入新元素的步骤：

　　寻找元素合适的插入位置：新元素与当前结点进行比较，若值大于当前结点，则从右子树进行寻找；否则从左子树进行寻找。
　　找到插入位置之后，以元素的值构建新节点，插入二叉排序树中。

具体代码实现：

/*insert(T key)*/

template <typename T>
void BSTree<T>::insert(T key)
{
    BSNode<T>* pparent = NULL;  //要插入节点的父节点
    BSNode<T>* pnode = root;
    /*先找到能插入的位置,即此节点的父节点*/
    while(pnode!=NULL)
    {
        pparent = pnode;
        if(key < pnode -> value)
            pnode = pnode -> lchild;
        else if(key > pnode -> value)
            pnode = pnode -> rchild;
        else 
            break;
    }

    /*以元素的值构建新节点*/
    pnode = new BSNode<T>(key);

    /*空树,新节点即为根节点*/
    if(pparent == NULL)
    {
        root = pnode;
    }
    else //不是空树
    {
        if(key < pparent->value)
            pparent -> lchild = pnode;  //新节点为左孩
        else
            pparent -> rchild = pnode;
    }
    pnode -> parent = pparent;          //指定新节点的父节点
};

2. 遍历

遍历三种方式前面讲过，这里直接上代码

/*前序遍历*/
template <typename T>
void BSTree<T>::preOrder(BSNode<T>* pnode)
{
    if(pnode != NULL)
    {
        cout << pnode -> value << endl;
        preOrder(pnode -> lchild);
        preOrder(pnode -> rchild);
    }
};
template <typename T>
void BSTree<T>::preOrder()
{
    preOrder(root);
};

/*中序遍历*/
template <typename T>
void BSTree<T>::inOrder(BSNode<T>* pnode)
{
    if(pnode != NULL)
    {
        inOrder(pnode -> lchild);
        cout << pnode -> value << endl;
        inOrder(pnode -> rchild);
    }
};

template <typename T>
void BSTree<T>::inOrder()
{
    inOrder(root);
};

/*后序遍历*/
template <typename T>
void BSTree<T>::postOrder(BSNode<T> *pnode)
{
    if(pnode != NULL)
    {
        postOrder(pnode -> lchild);
        postOrder(pnode -> rchild);
        cout << pnode -> value << endl;   
    }
};
template <typename T>
void BSTree<T>::postOrder()
{
    postOrder(root);
};

3. 删除节点

删除二叉排序树的某个节点有三种情况：

1. 被删除节点同时有左子树与右子树。
2. 被删除节点只有左子树或只有右子树。
3. 被删除节点没有子树。

对于第一种情况，我们的处理方式是将前驱节点的值保存在当前结点，继而删除前驱节点。
对于第二种情况，我们直接用子树替换被删节点。
对于第三种情况，我们可以直接删除节点。

删除节点的代码

/*删除某个节点*/
template <typename T>
void BSTree<T>::remove(BSNode<T>* pnode,T key)
{
    BSNode<T> *pdel = NULL, *ppre = NULL,*pnow = pnode,*s,*q;
    while(pnow != NULL)
    {
        if(pnow -> value == key)
            break;
        //ppre 被删节点的父节点
        ppre = pnow;
        if(pnow -> value > key)
            pnow = pnow -> lchild;
        else
            pnow = pnow -> rchild;
    }//找到要被删除节点

    if(pnow == NULL)
        return ;

    if(pnow -> lchild == NULL)
    {
        if(ppre == NULL)
            root = pnow -> rchild;
        else if(ppre -> lchild == pnow)
            ppre -> lchild = pnow -> rchild;
        else
            ppre -> rchild = pnow -> rchild;
        delete pnow;
        pnow = NULL;
    }
    else
    {
        //s 前驱节点
        q = pnow;
        s = pnow -> lchild;
        while(s -> rchild != NULL)
        {
            q = s;
            s = s -> rchild;
        }

        if(q == pnow)
            q -> lchild = s -> lchild;
        else
            q -> rchild = s -> lchild;

        pnow -> value = s -> value;
        delete s;
        s = NULL;
    }
};
template <typename T>
void BSTree<T>::remove(T key)
{
    remove(root,key);
};

4. 查找元素

查找元素的方式有递归和非递归两种，原理就是将要查找的元素的值与当前节点的值就行比较。如果要查找元素的值小于当前节点的值，就在当前节点的左子树中继续查找；如果值大于当前节点的值，就在当前节点的右子树中继续查找。

/*根据指定节点值查找节点－－非递归实现*/

template <typename T>
BSNode<T>* BSTree<T>::search__iterator(T key)
{
    BSNode<T>* pnode = root;
    while(pnode != NULL)
    {
        if(pnode -> value == key)
            return pnode;
        else if(pnode -> value > key)
            pnode = pnode -> lchild;
        else
            pnode = pnode -> rchild;
    }
    return NULL;
};

/*根据指定节点值查找节点－－递归实现*/
template <typename T>
BSNode<T>* BSTree<T>::search(BSNode<T>*& pnode,T key)
{
    if(pnode == NULL)
        return NULL;
    if(key == pnode -> value)
        return pnode;
    //在这打印　节点值，可查看查找顺序
    cout << "-----> " << pnode -> value << endl;
    if(key < pnode -> value)
        return search(pnode -> lchild,key);

    return search(pnode -> rchild,key);
};
template <typename T>
BSNode<T>* BSTree<T>::search_recursion(T key)
{
    return search(root,key);
};

5. 查找最值

最大值位于最右节点上，最小值位于最左节点上，递归搜索左右子树

/*查找最大元素*/

template T>
T BSTree<T>::search_maxnum(BSNode<T>* pnode)
{
    if(pnode -> rchild != NULL)
        return search_maxnum(pnode -> rchild);
    return pnode -> value;
};
template T>
T BSTree<T>::search_maxnum()
{
    return search_maxnum(root);
};

/*查找最小元素*/

template T>
T BSTree<T>::search_minnum(BSNode<T>* pnode)
{
    if(pnode -> lchild != NULL)
        return search_minnum(pnode -> lchild);
    return pnode -> value;
};
template T>
T BSTree<T>::search_minnum()
{
    return search_minnum(root);
};

6. 销毁二叉树

使用后序遍历递归销毁二叉查找树

template <typename T>
void BSTree<T>::destory(BSNode<T>* &pnode)
{
    if(pnode != NULL)
    {
        if(pnode -> lchild != NULL)
            destory(pnode -> lchild);
        if(pnode -> rchild != NULL)
            destory(pnode -> rchild);
        delete pnode;
        pnode = NULL;
    }
};
template <typename T>
void BSTree<T>::destory()
{
    destory(root);
};

7. 代码测试

int main()
{
    BSTree tree;
    BSNode * pnode;
    tree.insert(10);
    tree.insert(20);
    tree.insert(30);
    tree.insert(40);
    tree.insert(25);
    tree.insert(100);
    tree.insert(60);
    tree.insert(55);

    tree.inOrder();
    cout << "查找顺序为：" << endl;
    pnode = tree.search_recursion(55);
    cout << pnode -> value << endl;
    cout << "最大值为：" << tree.search_maxnum() << endl;
    cout << "最小值为　" << tree.search_minnum() << endl;
    tree.remove(100);
    tree.inOrder();
    return 0;
}

8. 输出结果

中序遍历：
10
20
25
30
40
55
60
100
查找值为55 的节点　查找顺序为：
-----> 10
-----> 20
-----> 30
-----> 40
-----> 100
-----> 60
55
最大值为：100
最小值为　10
删除节点后，再次中序遍历：
10
20
25
30
40
55
60

结束