数据结构与算法(十)深度优先搜索与广度优先搜索
广度优先搜索
广度优先搜索:从一个顶点出发(由开始时顶点创造顺序优先决定),访问所有没有被访问过的临节点。然后在从被访问过的节点出发,重复之前的操作
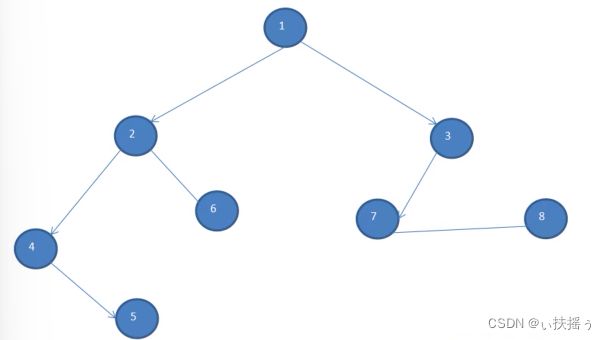
如下为一个图
从1出发,先后访问2 3,之后2访问它的邻接点4,3访问它的邻接点5(因为4已经被访问过了,所有节点只访问一次),最后4访问6,因为5的邻接点4 6访问过了,所以5不再访问6.
由该途径可以得到一个树,叫做广度优先生成树, 如下图所示
该存储路径由一个队列的形式和一个辅助数组存储该点是否被访问

1已经出队,所以数组1位置存储true,此时入队1的邻接点2 3,此后每出列一个邻接点,该邻接点的邻接点入列,数组相应的存储true,直到最后一个邻接点出列,算法结束
图有两种状态:连通和不连通,图中各顶点不一定要连接
所有节点都有连接叫做连通图,否则叫做不连通图
如下有两个图,同样可以当作一个图处理,也可以广度优先遍历
深度优先搜索
深度优先搜索:类似于黏菌走迷宫,先沿一条路走,无路可走时再回退
如下图:
首先从顶点1开始,走到2(可以能走3),然后走4,5,此时发现无路可走,退回4,发现4走过了,回到2,发现6没有走,就走6,然后回到2,回到1,1的右侧路同左侧路一致,3 7 8直到走完
在以上路线中依然有相应的数组去辅助访问,true或者false
此路径仍然可以以一个树来进行表示,叫做深度优先生成树:
该存储路径可由一个栈的形式和一个辅助数组存储该点是否被访问,现不具体表示
广度优先搜索代码实现
具体代码需要包含头文件
应用:
std::queue
Q.push(12); 传入12
std::cout << Q.front() << std::endl;打印队列首位元素
Q.pop(); 弹出队列首位
Q.empty(); 检查队列是否为空
代码实现:
需要包含的头文件如下
#include
#include
const int g_MaxCount = 100; 顶点最大值
bool visited[g_MaxCount]; 访问标志数组
typedef struct 存储数据
{
char Vex[g_MaxCount]; 顶点
int Edge[g_MaxCount][g_MaxCount]; 边
int VexCount; 顶点总数
int EdgeCount; 边总数
}AMGraph;
int locatecex(AMGraph G, char x) 查找顶点下标
{
for (size_t i = 0; i < G.VexCount; i++)
{
if (x == G.Vex[i])
{
return i;
}
}
return -1; 如果没有找到返回-1
}
void Create(AMGraph & G) 创建一个有向图的邻接矩阵
{
std::cout << "G.VexCount" << std::endl;
std::cin >> G.VexCount; 输入顶点总数
std::cout << "G.EdgeCount" << std::endl;
std::cin >> G.EdgeCount; 输入边总数
for (size_t i = 0; i < G.VexCount; i++)
{
std::cin >> G.Vex[i]; 存储顶点
}
for (size_t i = 0; i < G.VexCount; i++)
{
for (size_t j = 0; j < G.VexCount; j++)
{
G.Edge[i][j] = 0; 邻接矩阵内容全部初始化为0
}
}
char cStart;
char cEnd; 两个临时变量
int nStartIndex;
int nEndIndex; 存储获取后的下标
while (G.EdgeCount--)
{
std::cin >> cStart >> cEnd;
nStartIndex = locatecex(G, cStart);
nEndIndex = locatecex(G, cEnd);
if (nStartIndex != -1 && nEndIndex != -1)
{
//G.Edge[nStartIndex][nEndIndex] = G.Edge[nEndIndex][nStartIndex] = 1;无向图情况
G.Edge[nStartIndex][nEndIndex] = 1;有向图情况
}
else
{
G.EdgeCount++; 输入错误的情况下,让该循坏的参数再次加1回到之前状态
}
}
}
void BFS(AMGraph G, int nIndex) 遍历 传入图和下标
{
int QHeadValue; 一临时变量
std::queue
visited[nIndex] = true; 表示当前顶点已经被访问
Q.push(nIndex); 使数组相应位置元素加入队列
while (!Q.empty()) 队列不空的情况下
{
QHeadValue = Q.front(); 存储元素的值
Q.pop(); 弹出队列该值
for (size_t i = 0; i < G.VexCount; i++)
{
if (G.Edge[QHeadValue][i] && !visited[i])
{
std::cout << G.Vex[i] << "\t"; 输出传入图下标
visited[i] = true;
Q.push(i); 传入队列中
}
}
}
}
void print(AMGraph G) 遍历输出该图
{
for (size_t i = 0; i < G.VexCount; i++)
{
for (size_t j = 0; j < G.VexCount; j++)
{
std::cout << G.Edge[i][j] << "\t";
}
std::cout << std::endl;
}
}
int main()
{
char szBuffer;
AMGraph G;
Create(G);
print(G);
std::cout << "input start node:" << std::endl;
std::cin >> szBuffer; 输入遍历图的起点
int nIndex = locatecex(G, szBuffer); 接受该起点获取下标
if (nIndex != -1)
{
BFS(G, nIndex);
}
system("pause");
return 0;
}
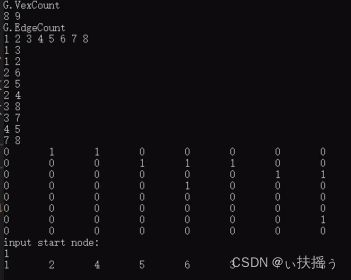
运行结果如下:包括遍历结果和邻接矩阵

深度优先搜索代码实现
具体代码实现同广度大致相同
需要包含的头文件如下
#include
#include
const int g_MaxCount = 100;//顶点最大值
bool visited[g_MaxCount];//访问标志数组
typedef struct {
char Vex[g_MaxCount];
int Edge[g_MaxCount][g_MaxCount];
int VexCount;
int EdgeCount;
}AMGraph;
int locatecex(AMGraph G, char x)
{
for (size_t i = 0; i < G.VexCount; i++)
{
if (x == G.Vex[i])
{
return i;
}
}
return -1;
}
void Create(AMGraph & G)
{
std::cout << "G.VexCount" << std::endl;
std::cin >> G.VexCount;
std::cout << "G.EdgeCount" << std::endl;
std::cin >> G.EdgeCount;
for (size_t i = 0; i < G.VexCount; i++)
{
std::cin >> G.Vex[i];
}
for (size_t i = 0; i < G.VexCount; i++)
{
for (size_t j = 0; j < G.VexCount; j++)
{
邻接矩阵内容全部初始化为0
G.Edge[i][j] = 0;
}
}
char cStart;
char cEnd;
int nStartIndex;
int nEndIndex;
while (G.EdgeCount--)
{
std::cin >> cStart >> cEnd;
nStartIndex = locatecex(G, cStart);
nEndIndex = locatecex(G, cEnd);
if (nStartIndex != -1 && nEndIndex != -1)
{
//G.Edge[nStartIndex][nEndIndex] = G.Edge[nEndIndex][nStartIndex] = 1;
G.Edge[nStartIndex][nEndIndex] = 1;
}
else
{
G.EdgeCount++;
}
}
}
void DFS(AMGraph G, int nIndex) 算法同广度有所修改
{
std::cout << G.Vex[nIndex] << "\t"; 打印当前节点
visited[nIndex] = true;
for (size_t i = 0; i < G.VexCount; i++)
{
if (G.Edge[nIndex][i] && !visited[i])
{
DFS(G, i); 递归
}
}
}
void print(AMGraph G)
{
for (size_t i = 0; i < G.VexCount; i++)
{
for (size_t j = 0; j < G.VexCount; j++)
{
std::cout << G.Edge[i][j] << "\t";
}
std::cout << std::endl;
}
}
int main()
{
char szBuffer;
AMGraph G;
Create(G);
print(G);
std::cout << "input start node:" << std::endl;
std::cin >> szBuffer;
int nIndex = locatecex(G, szBuffer);
if (nIndex != -1)
{
DFS(G, nIndex);
}
system("pause");
return 0;
}
运行结果如下: