【105】从前序与中序遍历序列构造二叉树
目录标题
- 一、题目
- 二、思路
- 代码
-
- 1
- 2
- 3
一、题目
二、思路
前序遍历:根左右 中序遍历:左根右

就不太明白从数组到树的递归怎么写,递归参数是什么,于是看了下评论的解答,自己理解了下

然后具体的范围确定,这里细节有两个点纠结了很久:
(1)先序遍历的左右子树范围切片点
(2)中序遍历的左子树起点为什么不能一直是0
这两个点待会会在bug调试里提到。先讲一下正确的思路:
接下来就是具体的范围确定。
(1)先序第一个值为根值
(2)在中序中找到a[i]=num,则[l2,i-1]为左树,[i+1,r2]为右树
(3)在先序中确定左右树范围:
中序中可以确定左树的节点数量:i-1-l2,先序的分割点假设是x,则先序中左树数量是x-l1-1(第一个点是根要-1)则有
i-1-l2=x-l1-1,求得x=i+l1-l2。
所以先序的左树范围就是[l1,x=i+l1-l2],右树范围是[i+l1-l2+1,r1]。
关于范围:
root.left = Tree(preorder,L1+1,L1+j-L2,inorder,L2,j-1,map);
root.right=Tree(preorder,L1+j-L2+1,R1,inorder,j+1,R2,map);
因为要想到这样算分割点实在有点难,受评论启发,定义一个中间变量来表示左子树的个数,这样就好理解多了.
int num = j-1-L1;
root.left = Tree(preorder,L1+1,L1+1+num,inorder,L2,j-1,map);
root.right=Tree(preorder,L1+1+num+1,R1,inorder,j+1,R2,map);
但是刚刚发现执行了一下会出现问题欸
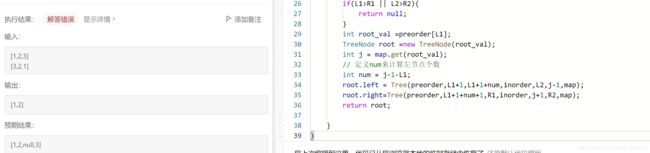
有点晚了,之后再认真看下代码吧。那就按照原来的算吧。
代码
1
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder==null|| inorder==null){
return null;
}
// int L1 = preorder.length;
// int L2 = inorder.length;
// TreeNode tree =Tree(0,L1,0,L2,preorder,inorder);
return Tree(0,preorder.length-1,0,inorder.length-1,preorder,inorder);
}
public TreeNode Tree( int preorder_left,int preoder_right, int inorder_left, int inorder_right,int[] preorder, int[] inorder)
{
if (preorder_left > preoder_right){
return null;
}
int num=preorder[preorder_left];
int a = inorder_left;
while(inorder[a]!=num){
a++;
}
// int a=0;
// for(int j=inorder_left;j<inorder_right;j++){
// if(inorder[j]==num){
// a=j;
// break;
// }
// }
TreeNode root = new TreeNode(num);
// root.left = Tree(preorder_left+1,,inorder_left,a-1,preorder,inorder);
// root.right = Tree(preorder_left+a,preorder.length-1,a+1,inorder.length-1,preorder,inorder);
root.left = Tree(preorder_left+1,preorder_left + a - inorder_left,inorder_left,a-1,preorder,inorder);
root.right = Tree(preorder_left + a - inorder_left+ 1,preoder_right,a+1,inorder_right,preorder,inorder);
return root;
}
}
遍历会提高时间复杂度:
以空间换时间,先将中序遍历序列转换成一个hashMap
2
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
HashMap<Integer,Integer> map =new HashMap<>();
for (int i=0 ;i<inorder.length;i++){
map.put(inorder[i],i);
}
return Tree(preorder,0,preorder.length-1,inorder,0,preorder.length-1,map);
}
public TreeNode Tree(int[] preorder,int L1,int R1,int[] inorder,int L2,int R2 ,HashMap<Integer,Integer> map){
if(L1>R1 || L2>R2){
return null;
}
int root_val =preorder[L1];
TreeNode root =new TreeNode(root_val);
int j = map.get(root_val);
root.left = Tree(preorder,L1+1,L1+j-L2,inorder,L2,j-1,map);
root.right=Tree(preorder,L1+j-L2+1,R1,inorder,j+1,R2,map);
return root;
}
}
3
贴一个评论的有趣代码
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder.length==0||inorder.length==0){
return null;
}
TreeNode root=new TreeNode (preorder[0]);
for(int i=0;i<preorder.length;i++){
if(preorder[0]==inorder[i]){
root.left=buildTree(Arrays.copyOfRange(preorder,1,i+1),Arrays.copyOfRange(inorder,0,i));
root.right=buildTree(Arrays.copyOfRange(preorder,i+1,preorder.length),Arrays.copyOfRange(inorder,i+1,inorder.length));
break;
}
}
return root;
}
}
Arrays.copyOfRange(preorder,i+1,preorder.length)#复制一个左闭右开的数组
为什么两个的范围不一样,是因为它实现了一个动态copy的是[1,i+1]就已经把第一个元素(根)删除了,然后因为根在第一次的位置是I 所以左数个数是i-1,copyOfRange 左闭合右开,刚好是一样的
为什么上面那个递归需要算个数呢
i-1-l2=x-l1-1,求得x=i+l1-l2。
是因为传入的是原数组,每次先序的左边界是不一样的。
缺点:copyOfRange 消耗资源,双指针节省空间内存