非线性方程求根迭代法(C++)
文章目录
- 问题描述
- 算法描述
-
- 不动点迭代法
-
- 一维情形
- 多维情形
- 牛顿迭代法
-
- 单根情形
- 重根情形
- 割线法
- 抛物线法
- 逆二次插值法
- 算法实现
-
- 准备工作
- 一般迭代法
- 割线法
- 抛物线法
- 逆二次插值法
- 实例分析
-
- 例1
- 例2
迭代法是一种求解非线性方程根的方法, 它通过构造一个迭代过程, 将一个非线性方程转化为一个等价的不动点方程, 然后通过迭代逼近不动点, 从而得到非线性方程的根.
迭代法的基本思想是将隐式方程转化为显式的计算公式, 然后通过迭代, 求方程近似根.
问题描述
已知方程
f ( x ) = 0 \bm f(\bm x)=\bm 0 f(x)=0
在 R n \mathbb R^n Rn的某个区域 D D D上有根, 求方程的近似解 x \bm x x.
算法描述
迭代法要求将上述方程化为如下形式:
x n + 1 = φ ( x n ) \bm x_{n+1}=\bm\varphi(\bm x_n) xn+1=φ(xn)
则可取 φ \bm\varphi φ为迭代函数. 而迭代函数的构造方式并不是唯一的, 不同算法的构造方式不同, 下面将逐个进行介绍.
不动点迭代法
不动点迭代法是一种求解非线性方程的数值方法, 其基本思想是将原方程变形为关于 x x x的迭代方程, 然后通过不断迭代求解 x x x的值.
一维情形
假设有非线性方程
f ( x ) = 0 f(x)=0 f(x)=0
则可以通过恒等变形改写为
x = φ ( x ) x=\varphi(x) x=φ(x)
因此, 我们可以得到如下不动点迭代公式:
x n + 1 = φ ( x n ) x_{n+1}=\varphi(x_n) xn+1=φ(xn)
故求解原方程的解就转化为求解函数 φ ( x ) \varphi(x) φ(x)的不动点. 设 x 0 x_0 x0为方程的一个近似解, 则利用上述不动点迭代公式即可逼近原方程的解.
多维情形
在一维情形的基础下, 进一步考虑非线性方程组
f ( x ) = 0 \bm f(\bm x)=\bm 0 f(x)=0
和一维情形类似, 可将方程变形为
x = φ ( x ) \bm x=\bm\varphi(\bm x) x=φ(x)
故有高维不动点迭代公式:
x n + 1 = φ ( x n ) \bm x_{n+1}=\bm\varphi(\bm x_n) xn+1=φ(xn)
牛顿迭代法
牛顿迭代法(Newton-Raphson method)是求解方程近似根的一种方法, 其基本思想是利用泰勒公式将方程进行线性化, 然后通过不断迭代, 使得误差逐渐缩小, 最终得到近似解.
单根情形
首先, 将 f ( x ) f(x) f(x)在 x = x 0 x=x_0 x=x0处进行泰勒展开, 得到
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ( x − x 0 ) 2 + ⋯ f(x) = f(x_0) + f^{\prime}(x_0)(x-x_0) + \frac{f^{\prime\prime}(x_0)}{2}(x-x_0)^2 + \cdots f(x)=f(x0)+f′(x0)(x−x0)+2f′′(x0)(x−x0)2+⋯
其中 f ′ ( x ) f^{\prime}(x) f′(x)和 f ′ ′ ( x ) f^{\prime\prime}(x) f′′(x)分别表示 f ( x ) f(x) f(x)在 x x x处的导数和二阶导数.
令
e ( x ) = f ( x ) f ′ ( x ) e(x) = \frac{f(x)}{f^{\prime}(x)} e(x)=f′(x)f(x)
则有
e ( x ) = − f ( x 0 ) f ′ ( x 0 ) − ( x − x 0 ) − f ′ ′ ( x 0 ) 2 f ′ ( x 0 ) ( x − x 0 ) 2 − ⋯ e(x) = - \frac{f(x_0)}{f^{\prime}(x_0)} - (x-x_0) - \frac{f^{\prime\prime}(x_0)}{2f^{\prime}(x_0)}(x-x_0)^2 - \cdots e(x)=−f′(x0)f(x0)−(x−x0)−2f′(x0)f′′(x0)(x−x0)2−⋯
因此, 可以通过迭代公式
x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1} = x_n - \frac{f(x_n)}{f^{\prime}(x_n)} xn+1=xn−f′(xn)f(xn)
不断迭代求解, 直到 e ( x ) e(x) e(x)的值足够小(即达到所需的精度), 即可得到方程的近似解.
值得注意的是, 牛顿迭代法的前提是方程的导数, 即 f ′ ( x ) f^{\prime}(x) f′(x)在所求解的区间内不等于零, 否则会导致方法失效. 此外, 迭代过程中可能会出现震荡或收敛于非解的情况, 此时需要采取适当的策略进行优化和调整.
重根情形
若 x 0 x_0 x0为 f ( x ) f(x) f(x)的根, 且其重数大于 1 1 1, 此时 f ( x 0 ) f(x_0) f(x0)和 f ′ ( x 0 ) f^\prime(x_0) f′(x0)都为 0 0 0, 这给牛顿法和后面的割线法都带来了问题, 因为在它们的公式分母中都包含导数或其估算值, 当解收敛到离根非常近时, 可能会导致除零错误.
对此, 我们可以令
u ( x ) = f ( x ) f ′ ( x ) u(x)=\frac{f(x)}{f^\prime(x)} u(x)=f′(x)f(x)
则可以证明: 若 x 0 x_0 x0为原方程的 m m m重根, 则其为方程
u ( x ) = 0 u(x)=0 u(x)=0
的单根, 从而对 u ( x ) = 0 u(x)=0 u(x)=0应用牛顿迭代法即可.
割线法
设 f : R → R f:\mathbb R\rightarrow\mathbb R f:R→R, 但函数 f f f的性质不好, 可能在某些地方不可导或导数难以计算. 这时我们就可以利用割线近似切线, 即
f ′ ( x n ) ≈ f ( x n ) − f ( x n − 1 ) x n − x n − 1 f^\prime(x_n)\approx\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}} f′(xn)≈xn−xn−1f(xn)−f(xn−1)
代入牛顿迭代公式, 就得到了割线法:
x k + 1 = x k − x n − x n − 1 f ( x n ) − f ( x n − 1 ) f ( x k ) x_{k+1}=x_k-\frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}f(x_k) xk+1=xk−f(xn)−f(xn−1)xn−xn−1f(xk)
抛物线法
抛物线法又称为米勒法, 是割线法的推广. 割线法是利用前两项构造线性插值, 而抛物线法则是利用前三项构造二次插值, 则我们可以求得如下迭代公式:
x k + 1 = x k − 2 f k ω + s g n ( ω ) ω 2 − 4 f k f [ x k , x k − 1 , x k − 2 ] x_{k+1}=x_k-\frac{2f_k}{\omega+{\rm sgn}(\omega)\sqrt{\omega^2-4f_kf[x_k,x_{k-1},x_{k-2}]}} xk+1=xk−ω+sgn(ω)ω2−4fkf[xk,xk−1,xk−2]2fk
其中,
ω = f k − f k − 1 x k − x k − 1 + x k − x k − 1 x k − x k − 2 ( f k − f k − 1 x k − x k − 1 − f k − 1 − f k − 2 x k − 1 − x k − 2 ) \omega=\frac{f_k-f_{k-1}}{x_k-x_{k-1}}+\frac{x_k-x_{k-1}}{x_k-x_{k-2}}\left(\frac{f_k-f_{k-1}}{x_k-x_{k-1}}-\frac{f_{k-1}-f_{k-2}}{x_{k-1}-x_{k-2}}\right) ω=xk−xk−1fk−fk−1+xk−xk−2xk−xk−1(xk−xk−1fk−fk−1−xk−1−xk−2fk−1−fk−2)
逆二次插值法
在抛物线法中, 当构造的抛物线不与 x x x轴相交时, 可能会收敛到方程的复数根. 这一方面体现了抛物线法的一个优点: 实的初始值迭代求得方程的复数根; 但同时也有可能无法收敛到实数根. 使用逆二次插值法可以解决这个问题.
逆二次插值法又称为反抛物线法, 即使用以 y y y为自变量的抛物线 x = g ( y ) x=g(y) x=g(y)与横轴的交点逼近函数 f ( x ) f(x) f(x)的实根. 可计算得迭代公式如下:
x k + 1 = x k − y k x k − x k − 1 y k − y k − 1 + y k y k − 1 y k − y k − 2 ( x k − x k − 1 y k − y k − 1 − x k − 1 − x k − 2 y k − 1 − y k − 2 ) x_{k+1}=x_k-y_k\frac{x_k-x_{k-1}}{y_k-y_{k-1}}+\frac{y_ky_{k-1}}{y_k-y_{k-2}}\left(\frac{x_k-x_{k-1}}{y_k-y_{k-1}}-\frac{x_{k-1}-x_{k-2}}{y_{k-1}-y_{k-2}}\right) xk+1=xk−ykyk−yk−1xk−xk−1+yk−yk−2ykyk−1(yk−yk−1xk−xk−1−yk−1−yk−2xk−1−xk−2)
算法实现
准备工作
由于牵涉到高维问题, 我们首先编写一个向量之间的度量函数:
double distance(const std::vector<double> &x, const std::vector<double> &y)
{
size_t n(x.size());
if (!n)
return 0;
if (n != y.size())
return NAN;
double r(0);
auto i = x.cend(), j = y.cend();
do
{
double t(*--i - *--j);
r += t *= t;
} while (--n);
return sqrt(r);
}
由于抛物线法中涉及到符号函数, 另外编写符号函数sgn:
// 符号函数
template <class T>
inline int sgn(const T &x) noexcept
{
if (x == 0)
return 0;
if (x > 0)
return 1;
return -1;
}
此外, 为了方便用户输入函数, 还要编写一个字符串替换的函数:
/*
* 替换子串
* str : 要替换的字符串
* oldStr: 旧子串
* newStr: 新子串
* except: 排除的子串
*/
std::string &substring_replace(std::string &str, const std::vector<std::string> &oldStr, const std::vector<std::string> &newStr, const std::vector<std::string> &except)
{
if (oldStr.empty())
{
str.clear();
return str;
}
// if(oldStr.size()!=newStr.size())
// if(oldStr.size()>newStr.size())
// oldStr.erase(oldStr.begin()+newStr.size(),oldStr.end());
// else
// newStr.erase(newStr.begin()+oldStr.size(),newStr.end());
size_t n(oldStr.size() > newStr.size() ? newStr.size() : oldStr.size());
QBitArray a(str.length()); // 这里用了Qt中的QBitArray, 使用bool数组也可以实现其功能
for (const auto &i : except)
{
size_t pos(0);
while ((pos = str.find(i, pos)) != std::string::npos)
{
a.fill(true, pos, pos + i.length());
pos += i.length();
}
}
size_t pos(0);
for (size_t k(0); k < n; ++k)
{
const std::string &pre = oldStr[k], &next = newStr[k];
F:
while ((pos = str.find(pre, pos)) != std::string::npos)
{
size_t i(pre.length()), p(pos);
do
if (a.at(p++))
{
pos += pre.length();
goto F;
}
while (--i);
QBitArray t(a.size() + next.size() - pre.size());
do
t.setBit(i, a.at(i));
while (++i < pos);
p = pos + pre.length();
str.replace(pos, pre.length(), next);
if (i != (pos += next.length()))
do
t.setBit(i, false);
while (++i != pos);
while (p != a.size())
t.setBit(i++, a.at(p++));
a = t;
}
}
return str;
}
以及浮点向量转字符串向量的函数:
// double向量转string向量
std::vector<std::string> vec_to_string(const std::vector<double> &x)
{
std::vector<std::string> y(x.size());
auto i = x.cbegin();
auto k = y.begin();
while (i < x.cend())
*k++ = *i++;
return y;
}
一般迭代法
为了方便用户输入, 我们首先引入字符串函数计算1:
extern double calStr(string);
extern double calStr_x(string, const double &);
vector<string> func{"sqrt", "sin", "log", "exp", "pow", "abs", "cos", "tan", "asin", "acos", "atan"};
接着实现一般迭代法的单步迭代:
/*
* 迭代法
* current_vec: 迭代向量
* func : 迭代函数
* x : 未知数
*
* 返回(bool):
* true : 迭代失败
* false: 迭代成功
*/
bool iterative_method(std::vector<double> ¤t_vec, const std::vector<std::string> &f, const std::vector<std::string> &x)
{
std::vector<double> x0(current_vec);
unsigned n(current_vec.size());
do
{
std::string toCal(f[--n]);
substring_replace(toCal, x, vec_to_string(current_vec), func);
if (isnan(current_vec[n] = calStr(toCal)))
{
current_vec = x0;
return true;
}
} while (n);
return false;
}
最终, 实现一般迭代法如下:
/*
* 迭代法
* current_vec: 迭代向量
* func : 迭代函数
* x : 未知数
* epsilon : 迭代终止条件
* mid : 迭代中间结果导出
*
* 返回(bool):
* true : 迭代失败
* false: 迭代成功
*/
bool iterative_method(std::vector<double> ¤t_vec, const std::vector<std::string> &func, const std::vector<std::string> &x, double epsilon, QString &mid) // mid使用了QString, 可以对应转换为std::string或者std::vector>
{
for (auto &i : x)
mid.append(QString::fromStdString(i)).append(',');
*(mid.end() - 1) = '\n';
for (auto &i : current_vec)
mid.append(QString::number(i, 'g', 14)).append(',');
std::vector<double> x0(current_vec), x1(x0);
if (iterative_method(current_vec, func, x))
{
current_vec = x0;
return true;
}
*(mid.end() - 1) = '\n';
for (auto &i : current_vec)
mid.append(QString::number(i, 'g', 14)).append(',');
while (distance(current_vec, x1) >= epsilon)
{
x1 = current_vec;
if (iterative_method(current_vec, func, x))
{
current_vec = x0;
return true;
}
*(mid.end() - 1) = '\n';
for (auto &i : current_vec)
mid.append(QString::number(i, 'g', 14)).append(',');
}
mid.chop(1);
return false;
}
割线法
/*
* 割线法
* f : 原方程函数
* x1 : 第1个值
* x2 : 第2个值
* e : 精度
* path: 迭代保存路径
*/
void secant_method(const function<double(double)> &f, double x1, double x2, double e = 1e-6, const QString &path = QStandardPaths::writableLocation(QStandardPaths::DesktopLocation))
{
QFile file(path);
if (!(file.open(QIODevice::WriteOnly)))
throw "文件保存失败!";
double f1(f(x1)), f2;
if (isnan(f1))
throw "区间内存在奇点!";
file.write((to_string(x1) + '\n' + to_string(x2)).c_str());
while (abs(x1 - x2) >= e)
{
if (isnan(f2 = f(x2)))
{
file.close();
throw "区间内存在奇点!";
}
double t = x2 - (x2 - x1) * f2 / (f2 - f1);
file.write(('\n' + to_string(t)).c_str());
x1 = x2;
x2 = t;
f1 = f2;
}
file.close();
}
抛物线法
/*
* 抛物线法
* f : 原方程函数
* x1 : 第1个值
* x2 : 第2个值
* x3 : 第3个值
* e : 精度
* path: 迭代保存路径
*/
void parabolic_method(const function<double(double)> &f, double x1, double x2, double x3, double e = 1e-6, const QString &path = QStandardPaths::writableLocation(QStandardPaths::DesktopLocation))
{
QFile file(path);
if (!(file.open(QIODevice::WriteOnly)))
throw "文件保存失败!";
double f1(f(x1)), f2(f(x2)), f3, omega0((f2 - f1) / (x2 - x1));
if (isnan(f1) || isnan(f2))
{
file.close();
throw "区间内存在奇点!";
}
file.write((to_string(x1) + '\n' + to_string(x2) + '\n' + to_string(x3)).c_str());
while (abs(x1 - x2) >= e)
{
if (isnan(f3 = f(x3)))
{
file.close();
throw "区间内存在奇点!";
}
double omega1 = (f3 - f2) / (x3 - x2), d123 = (omega1 - omega0) / (x3 - x1), omega = omega1 + (x3 - x2) * d123, delta = omega * omega - 4 * f3 * d123;
if (delta < 0)
{
file.close();
throw "迭代出现复根!";
}
double t = x3 - 2 * f3 / (omega + sgn(omega) * sqrt(delta));
file.write(('\n' + to_string(t)).c_str());
x1 = x2;
x2 = x3;
x3 = t;
f1 = f2;
f2 = f3;
omega0 = omega1;
}
file.close();
}
逆二次插值法
/*
* 逆二次插值法
* f : 原方程函数
* x1 : 第1个值
* x2 : 第2个值
* x3 : 第3个值
* e : 精度
* path: 迭代保存路径
*/
void inverse_quadratic_interpolation(const function<double(double)> &f, double x1, double x2, double x3, double e = 1e-6, const QString &path = QStandardPaths::writableLocation(QStandardPaths::DesktopLocation))
{
QFile file(path);
if (!(file.open(QIODevice::WriteOnly)))
throw "文件保存失败!";
double f1(f(x1)), f2(f(x2)), f3, omega0((x2 - x1) / (f2 - f1));
if (isnan(f1) || isnan(f2))
{
file.close();
throw "区间内存在奇点!";
}
file.write((to_string(x1) + '\n' + to_string(x2) + '\n' + to_string(x3)).c_str());
while (abs(x1 - x2) >= e)
{
if (isnan(f3 = f(x3)))
{
file.close();
throw "区间内存在奇点!";
}
double omega1 = (x3 - x2) / (f3 - f2), t = x3 - omega1 * f3 + (omega1 - omega0) * f3 * f2 / (f3 - f1);
file.write(('\n' + to_string(t)).c_str());
x1 = x2;
x2 = x3;
x3 = t;
f1 = f2;
f2 = f3;
omega0 = omega1;
}
file.close();
}
实例分析
例1
设有方程 x 3 + 2 x 2 + 10 x − 20 = 0 x^3+2x^2+10x-20=0 x3+2x2+10x−20=0.
首先计算出 f ′ ( x ) = 3 x 2 + 4 x + 10 f^\prime(x)=3x^2+4x+10 f′(x)=3x2+4x+10, 下面我们讨论选取不同初值时Newton迭代法的收敛速度.
分别取 x 0 ∈ { x ∈ Z : − 128 ⩽ x ⩽ 127 } x_0\in\{x\in\mathbb Z:-128\leqslant x\leqslant 127\} x0∈{x∈Z:−128⩽x⩽127}, 并取终止标准为 ∣ f ( x n ) ∣ < 1 0 − 6 |f(x_n)|<10^{-6} ∣f(xn)∣<10−6, 计算得其误差与迭代次数如下所示:
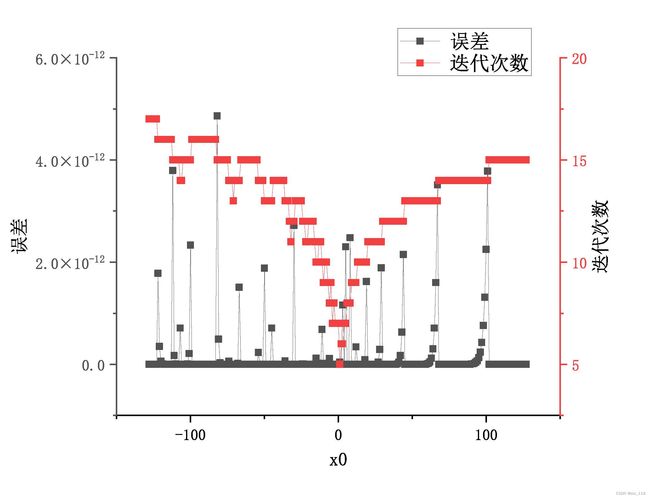
观察可得, 在 x 0 = 1 x_0=1 x0=1附近时迭代次数较少, 收敛较快, 接着在 1 1 1附近取更密集的初值, 计算结果如下所示:
x = − 2 3 − 13 4 3 3 3 3930 + 176 3 + 1 3 6 3930 + 352 3 = 1.36880 ⋯ x=-\frac23-\frac{13\sqrt[3]{4}}{3\sqrt[3]{3\sqrt{3930}+176}}+\frac13\sqrt[3]{6\sqrt{3930}+352}=1.36880\cdots x=−32−3333930+1761334+31363930+352=1.36880⋯
可见当初值越靠近根 x x x, 迭代次数越少, 收敛速度越快.
例2
取初值 x 0 = 4 , x 1 = 3.8 x_0=4,x_1=3.8 x0=4,x1=3.8, 求方程 x 3 − 2 x − 5 = 0 x^3-2x-5=0 x3−2x−5=0在 [ 1 , 4 ] [1,4] [1,4]上的根.
仍然取终止标准为 ∣ f ( x n ) ∣ < 1 0 − 6 |f(x_n)|<10^{-6} ∣f(xn)∣<10−6, 使用Newton迭代法可得误差为 − 1.77636 × 1 0 − 5 -1.77636\times10^{-5} −1.77636×10−5, 迭代次数为6次; 取终止标准为 ∣ x n + 1 − x n ∣ < 1 0 − 6 |x_{n+1}-x_n|<10^{-6} ∣xn+1−xn∣<10−6, 使用割线法可得误差为 2.37144 × 1 0 − 13 2.37144\times10^{-13} 2.37144×10−13, 迭代次数为8次.
参见C++实现简单计算器(字符串替换). ↩︎
