工序调度 （AOE Network | TAG | Online Alg | 关键路径 | 拓扑排序 | 瓶颈工序）

目录

  任务调度     

 AOE网

源点与汇点

关键活动与关键路径

相关概念

步骤如下：（结合代码理解）

代码

---

---

  任务调度     

        假定一个工程项目由一组子任务构成，子任务之间有的可以并行执行，有的必须在完成了其它一些子任务后才能执行。“任务调度”包括一组子任务、以及每个子任务可以执行所依赖的子任务集。    

---

---

 AOE网

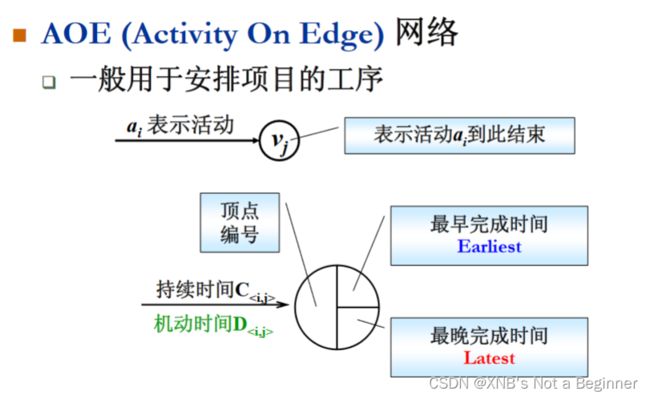
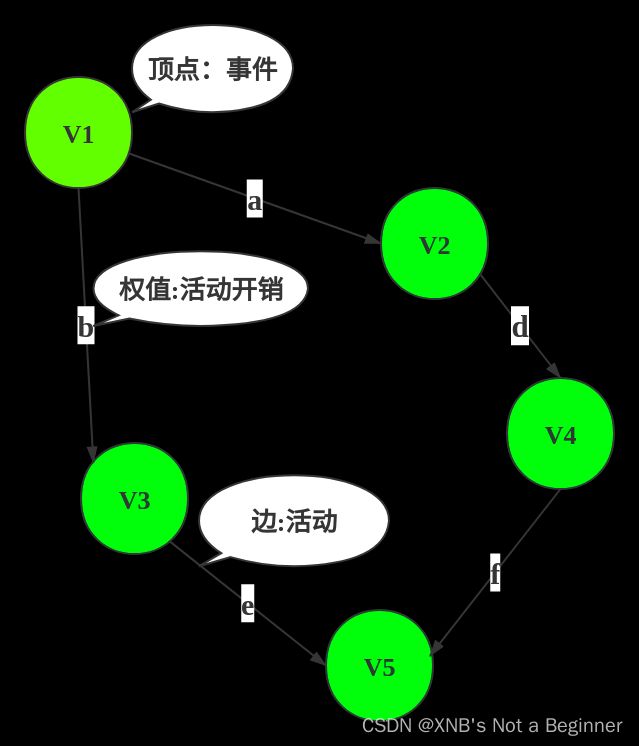
AOE网（Activity On Edge Network）用边表示活动，用顶点表示事件（活动的完成）。边是带权的，表示活动需要的时间。

---

源点与汇点

源点：入度为0的点，表示一个工程的开始。

汇点：出度为0的点，表示一个工程的结束。

---

关键活动与关键路径

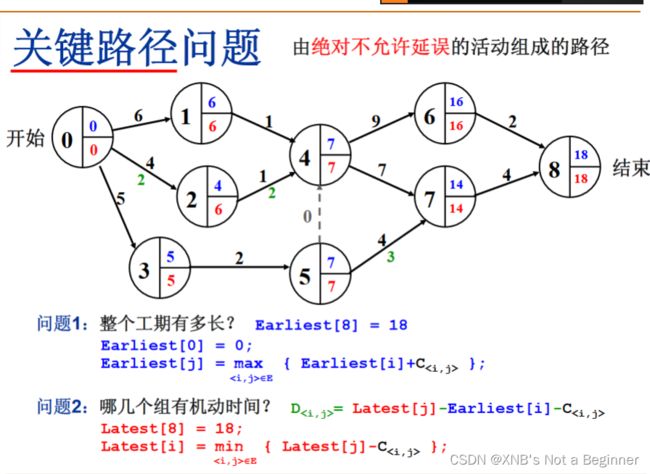
在AOE网中，从源点到汇点最长的路径称为关键路径，在关键路径上的活动称为关键活动。

因为AOE网中的活动是可以并行进行的，所以整个工程的时间开销，其实是最长路径的时间开销。即关键路径制约整个工程的工期。

        求关键路径我们只需要求出「活动最早发生时间」和「活动最晚发生时间」即可。

但是在 AOE 图中，「活动」就是向量边，求向量边一般是困难的，我们可以借助顶点来求边。

---

---

相关概念

• etv（Earliest Time of Vertex）：顶点最早发生时间，也就是「事件最早发生时间」
• ltv（Lastest Time of Vertex）：顶点最晚发生时间，也就是「事件最晚发生时间」
• ete（Earliest Time of Edge）：边最早发生时间，也就是「活动最早发生时间」
• lte（Lastest Time of Edge）：边最晚发生时间，也就是「活动最晚发生时间」

---

步骤如下：（结合代码理解）

我们通过 etv 求 ete，ltv 求 lte

• 通过拓扑排序求出 etv「事件最早发生时间」

etv[j] = max{etv(i) + weight}

• 通过「反向推导」求出 ltv「事件最晚发生时间」

ltv[i] = max{etv(j) - weight}

• 通过 etv 求出 ete「活动最早发生时间」

活动最早发生时间等于 from（箭头开始方向的事件最早发动时间）

• 通过 ltv 求出 lte「活动最晚发生时间」

活动最晚发生时间等于 to - weight（箭头结束方向的事件发生时间 - 权重）

• 通过 lte - ete 求出关键路径

---

代码

#include 
#include 
#include 
#include 
#include 
#include 

enum{EAR = 0,LAST = 1,
	UNDEF = -1,
	FOR = 0,BCK = 1,
	IN = 0,OUT = 1};
// EAR 最早完成时间 LAST 最晚
// FOR 正向分析 BCK 逆向分析 
// IN 入度 OUT 出度 
constexpr int NN { 10},/*项目*/ MM { NN * ( NN - 1 )}/*工序*/;
struct EDG {int ne,to,w,mot/*motile 机动时间*/;} edg[2][ MM ]/*流程*/;
int h[2][ NN ],/*头节点 
				0：正向|1：逆向*/	
	deg[2][ NN ],/*度
				0：入度|1：出度*/
	fin[2][ NN ],/*完成时间
				0：earliest最早完成时间
				1：lastest最晚完成时间*/
	tot[2] {0,},/*流程统计
				0：正向
				1：逆向*/
	Q[ NN << 2 | 1],f,b,
				/*模拟队列
				拓扑排序*/
	seq[2][ NN ][ NN ],
				/*工序
				0：正向
				1：逆向*/
	r = -1,c = 0,/*r工序层次
					c平行工序*/
	crtPa = 0,/*关键路径数目*/
	mlen = -1/*最大关键路径长度*/;

inline add(int x,int y,int z,int d){ /*加边 d = 0 正向
											d = 1 反向建边*/
	int (*_h)[ NN ] {&h[d]},
		*_tot {&tot[d],};
	EDG (*_edg)[ MM ] {&edg[d]};
	*( *_edg + (* _tot) ) = (EDG ){*( *_h + x ),y,z,0};
	*( *_h + x ) = ++(*_tot);
}
inline constexpr int min(int a,int b){return a < b?a:b;}
inline constexpr int max(int a,int b){return (a > b)?a:b;}
int (*cmptor[2])(int,int) = {max,min};
/*比较函数指针数组*/

_Bool jdg(int u,int L){
/*判断是否存在关键路径 
并且得到关键路径最大长度 关键路径条数*/
	int i,r = 1;
	for(i = h[FOR][u]; ~i ;i = edg[FOR][ i ].ne)
		if(edg[FOR][ i ].mot > 0 || ! ( r ^= jdg(edg[FOR][ i ].to,L+1) ))return 0;
	mlen = max(mlen,L);return (_Bool)( !!++crtPa );
}
int main(void){
	int N,M,
		x,y,z,
		i,j,k,e,t;
	scanf("%d%d",&N,&M);
	memset(h,-1,sizeof(int) * N);
	for(i = 0;i < 2;++i)
		memset(*(fin + i),0x3f,sizeof(int) * N);
	while(M -- && 
	~scanf("%d%d%d",&x,&y,&z)){
		for(i = 0;i < 2;++i)add(x,y,z,i);
		++deg[OUT][x],++deg[IN][y];
	}
	fin[FOR][0] = fin[BCK][0] = 0;//初始化 最早/最晚工期
	//topologsort 拓扑排序得到所有项目的最早/最晚完成时间 
	for(i = 0;i < 2;++i){ //i = 0 正向分析 得到 EAR 最早工期
							//i = 1 逆向分析 得到 LAST 最晚工期 
		f = 0,b = -1,r = -1,c = 0;
		for(j = 0;j < N;++j)if(!*( *(deg + i) + j ))
			Q[f++] = j;
		while(!(f == b+1)){
			k = f - b,c = 0,++r;
			while(k --){
				seq[i][r][c ++] = ( t = Q[++b] );
				for(e = h[i][ t ];~e;e = edg[i][ e ].ne){
					if(!*( *(deg + i) + edg[i][ e ].to ))
						Q[f++] = edg[i][ e ].to;
					fin[i][ edg[i][ e ].to ] = (*cmptor[i])(fin[i][ edg[i][ e ].to ],
						 fin[i][ t ] + edg[i][ e ].w);  
					}
				}
			}
		if(!i)fin[1-i][N - 1] = fin[i][N - 1];	
		}
	//得到机动时间 
	for(i = 0;i < N;++i)
		for(j = h[FOR][i];~j;j = edg[FOR][ j ].ne)
			edg[FOR][ j ].mot = !(fin[LAST][ edg[FOR][ j ].to ] - edg[FOR][ j ].w > 0)?-1:
						fin[LAST][ edg[FOR][ j ].to ] - fin[EAR][ i ] - edg[FOR][ j ].w;	
	printf("%s\n",jdg(0,0) ? "YES":"NO");	
	return 0;
}