优雅计算算式：后缀表达式

后缀表达式

提要

当用户输入了如同"10 - 2"这样的字符串，如何计算这个算式的算术结果？

答案似乎非常简单：遇到数字就缓存数字，遇到运算符，用缓存的数字对下一个数字进行操作就能得到结果。

对于"10 - 2 + 5"这样的序列，只需要做一点点修改：把上次的运算结果也缓存起来，跟上面的操作思路就一致了。

但是一遍线性扫描解决不了这样的问题：如何计算"10 - 2 * 5"？

按照运算符的优先级规则，我们必须先计算2*5才行，可是计算机只能线性扫描表达式。为此，我们不得不再扫描多几次：先扫描一遍，找出优先级最大的运算符，接着获取前、后的操作数，然后计算，并用计算结果替换这个运算式。然后再扫描一遍，计算，直到没有运算符为止…听起来就好麻烦。

这还没完，要是算式加上了括号：“5 * (10 - 2)”，这样减号的优先级就会高于乘号，反而需要先进行运算。我们可以这样实现：优先去括号，遇到括号的时候，增大里面每个运算符的优先级，接着去掉这层括号。然后就可以使用上面那个计算的算法（套路）啦。

是不是觉得这也太复杂了，一个算式要扫描这么多遍才能拿到结果，就没什么更简单的方法吗？

人类习以为常的中缀表示法看起来不太适合计算机理解。

中缀表示法

中缀表示法是指操作符以中缀形式处于操作数的中间（例：3 + 4）来表示算术或者逻辑公式的方法。既然有中缀，那也就有相应的前缀表示法和后缀表示法，它们又称波兰表达式和后缀表达式——也就是本文的主角。

顾名思义，前缀表达式嘛，运算符就得放前面，中缀的3+4表示为前缀就是+3 4，表示为后缀就是3 4+。

现实生活中不会拿前缀、后缀表示法来表示算式也许是因为，给你一个无分割的3755+，你根本不知道，它表达的到底是3+755还是37+55。

复杂一点的式子，表示出来就是这样：

5*(3+2) -> *5(+32) -> 5(32+)*

怎么感觉前缀、后缀表达式里的括号多余了？对，就是多余的，前缀、后缀表达式完全不需要括号来表示运算的优先级。（这也是这种表示法被提出的初衷——语法上不需要括号仍然能被无歧义地解析，用于简化命题逻辑）需要用括号来避免误解运算次序的只有中缀表达式。这不就简化了计算机处理括号的过程了吗？！

来个复杂的例子：5 + (18+3) * 5 - 2

后缀表示法：5 18 3 + 5 * + 2 -

前缀表示法： - + 5 * + 18 3 5 2

我们可以发现，后缀表达式里的运算符在去掉括号后，依然是按照正确的运算顺序排列的。先计算了18和3的+，再往后才是5的*。运算符从中缀转为后缀时已经有序，还顺带把加减/乘除法的优先级问题解决了。

似乎有点意思，使用不同的表示法之后，我们不知不觉就搞定运算符优先级的问题了！

三种表示法的内在联系——表达式二叉树

先看看表达式二叉树枯燥的定义：

概述

表达式二叉树(Binary expression tree)是用来表示表达式的一种特殊的二叉树。两种常见表达式是代数表达式（如：3+2）和布尔表达式（如true ^ false）都可以用它表示，这些表达式包含了一元运算符和二元运算符，从而节点的孩子可以是零个、一个或两个。表达式树的叶子节点储存操作数（操作数可以是常量或变量），而内部节点则储存运算符。这种受限制的结构简化了表达式树的处理。

表达式二叉树生成

如何从表达式生成一棵二叉树呢？暂时不从算法上进行探讨，而只是形式化地描述生成树的过程。

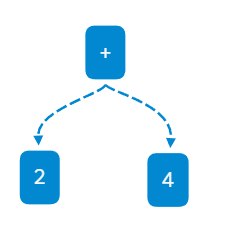
先思考最简单的算式：2+4，我们可以发现数字有两个，运算符却只有一个，而且恰好夹在数字中间（废话，这不是中缀表达式的特点吗？），生成的树就像下面这样：

接着我们变换一下式子：2+4-5，这个式子的树该怎么画呢？

不妨把2+4当作一个整体，作为一个数字来看待，那么很明显，我们可以拿减号来连接2+4这个整体表示的数和另一个数5，就像这样：

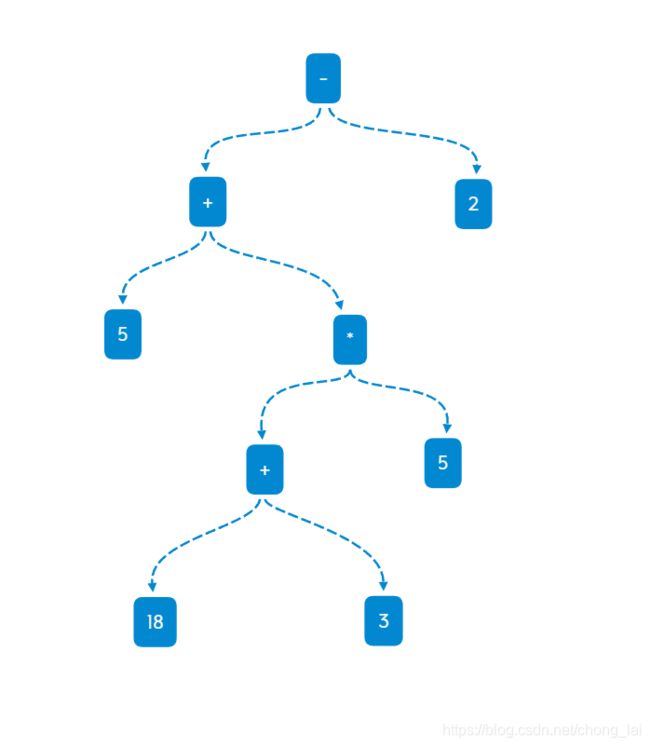
使用这种代换思想，稍加思索就可以生成5 + (18 + 3) * 5 - 2的表达式二叉树，确认好优先级最高的式子，生成一棵小树，再以这个为基础逐渐添砖加瓦，生成下面这样的树：

遍历

让我们以先序、中序、后序来遍历这颗树吧：

先序： - + 5 * + 18 3 5 2

中序：5 + 18 + 3 * 5 - 2

后序：5 18 3 + 5 * + 2 -

好巧，正对应了三种表示方式。不过中序遍历因为失去了括号的缘故，与原表达式产生了语义上的分歧，为此在遍历的时候就没办法像先序、后序那般省心，还要做额外的添加括号的判断。

我们看到了后缀表达式自动确定好运算符表达式的优势（为什么不是前缀？前缀表达式基本跟后缀表达式反着来，计算机需要从头扫描到尾，前缀不太好操作），接下来想要以后缀表达式的思路来计算，就得解决两个问题。

1. 如何将用户输入的中缀表达式转换成后缀表达式？
2. 如何计算后缀表达式的值？

Shunting Yard算法

接下来隆重介绍 Edsger Dijkstra提出的Shunting Yard（调度场）算法。这个算法进行一次扫描就能把中缀表达式转换为后缀表达式。

为了完成转换的任务，我们分别要用到一个输出队列和一个运算符缓存栈。

仍然是这个例子：5 + (18 + 3) * 5 - 2，计算机开始从左到右扫描每一个Character，并按照以下五条规则（完整的算法规则多一些，没关系，只讨论四则运算就能触类旁通）进行操作：

• 如果这个字符是一个数字，放进输出队列的队尾即可。

• 如果这个字符是一个左括号，无条件压入栈当中。

• 如果这个字符是个运算符，我们得把它放到栈中，不过得看情况：

  • 如果栈顶运算符优先级大于等于即将入栈的运算符，那么先把栈顶的运算符请出来，放到输出队列里面，循环进行，直到条件不满足。
  • 否则直接进栈。

• 如果这个字符是一个右括号，不断弹出栈内的运算符并放到输出队列里面，直到遇到左括号。左括号一样需要弹出，不过不要放在输出队列，抛弃即可。

• 扫描到尾部之后，如果栈非空，把运算符依次弹出，并放到输出队列里面。

最后依次取出输出队列的元素我们就可以把算式转换为后缀表达式。

全过程请看下面动图：

计算后缀表达式

既然已经把表达式转换成功了，接下来研究怎么计算自然是水到渠成。后缀表达式的计算比较简单，不过仍需要一个栈来缓存一下操作数，我们依次从刚才的队列中取出元素，然后：

• 如果是操作数，将其入栈。
• 如果是运算符，依次弹出栈内的两个数，然后就进行相应计算（注意符号是否满足交换律，后出栈的操作数是左操作数，先出栈的是右操作数），得出的计算结果进栈即可。

这样操作一番，栈内剩下的那个元素，就是你想要的最终结果。

完整过程如下：

怎么样，虽然还是有亿点点复杂（还没讨论诸如sin这样的函数），不过，至少比起强行让计算机在一遍遍的扫描中去理解中缀表达式更加轻松而优雅吧。

表达式二叉树的生成——算法浅析

这一节我们叙述如何用后缀表达式生成一棵表达式二叉树。

之所以把生成表达式二叉树的具体算法放到这里，是因为这个算法的核心思想与上方计算后缀表达式如出一辙，区别只有一点：我们把处于中间态的子树而不是显式的数值当作运算符的“运算结果”。

算法简述如下：

1. 初始化存储二叉树的栈，然后开始从左到右扫描后缀表达式。
2. 遇到操作数时，初始化为最小的二叉树（单个二叉树结点），然后入栈。
3. 遇到操作符时，初始化为二叉树结点，然后取出栈内的前两个子树，以该操作符为根结点，先出栈的作为右子树，后出栈的作为左子树，构造一棵新的二叉树，然后入栈。
4. 表达式扫描完毕后，栈内剩下唯一的一棵二叉树即为所求的表达式二叉树。

---

前缀表达式生成表达式二叉树的方法形式化叙述如下，栈内储存的不再是操作数，而是操作符，显得稍微复杂一些：

1. 初始化存储二叉树的栈，然后开始从左到右扫描前缀表达式。
2. 遇到运算符时，初始化为最小的二叉树（单个二叉树结点），然后入栈。
3. 遇到操作数时，初始化为二叉树结点，然后取出栈顶的二叉树，按照两种情况来操作：
   • 二叉树的根节点上没有左子树或者右子树，则将操作数结点放在左子树（如果没有左子树）或者右子树（如果有左子树）上。
   • 二叉树根节点左、右子树均有，则从栈内弹出一棵新的树B，把当前这颗树作为子树，添加到B树上（先左后右，左空优先放左），这之后，按照上一点来考虑操作数结点能不能加入到B树，如果不能，继续执行上述步骤，直到操作数成功进入二叉树内。
4. 表达式扫描完毕后，栈内剩下唯一的一棵二叉树即为所求的表达式二叉树。

至于中缀表达式，可以通过调度场算法来将中缀转为后缀来构造表达式二叉树。

Kotlin实现

以下给出了Kotlin版本的部分算法实现

Operator.kt

/**
 * 运算符的枚举类
 */
enum class Operator(val value: String, val priority: Int) {
    Plus("+", 1), Minus("-", 1),
    Multiply("*", 2), Divide("/", 2),
    Left("(", 3), Right(")", 3);

    override fun toString(): String {
        return value
    }

    companion object {
        /**
         * 将字符串映射为某一个确定的运算符
         */
        fun matching(value: String): Operator {
            return when(value) {
                "+" -> Plus
                "-" -> Minus
                "*" -> Multiply
                "/" -> Divide
                "(" -> Left
                ")" -> Right
                else -> Plus
            }
        }
    }
}

Utils.kt

/**
 * 将中缀表达式读入集合中，并以对象的形式储存
 * @param formula 中缀表达式字符串，其中操作数与操作符之间不含空格
 * @return 包含了操作数Int的对象和操作符Operator对象的集合，顺序与原来的中缀表达式一致
 */
fun getOperand(formula: String): List<Any> {
    val list: MutableList<Any> = mutableListOf()
    var begin = 0
    for (i in formula.indices) {
        val c = formula[i]
        // 如果c是一个运算符
        if (c.toString().matches(Regex("\\+|-|\\*|/|\\(|\\)"))) {
            // 按照缓存（begin）的起始位置到当前位置前，截断字符串，并解析成一个操作数
            val cache = formula.substring(begin, i)
            if (cache.isNotEmpty()) {
                list.add(cache.toInt())
            }
            // 将当前位置的字符解释为运算符
            list.add(Operator.matching(c.toString()))
            begin = i + 1
        }
    }
    // 解析表达式的最后一个操作数
    val sub = formula.substring(begin)
    if (sub.isNotEmpty()) {
        list.add(sub.toInt())
    }
    return list
}
/**
 * 将表示中缀表达式的集合转换为表示后缀表达式的队列，调度场算法
 */
fun generateReversePolishNotation(list: List<Any>): Queue<Any> {
    val operationStack: Stack<Operator> = Stack()
    val deque: ArrayDeque<Any> = ArrayDeque()
    for (any in list) {
        if (any is Double || any is Int) {
            // 操作数进队列
            deque.offerLast(any)
        } else if (any is Operator) {
            when (any) {
                Operator.Left -> {
                    // 左括号直接进栈
                    operationStack.push(any)
                }
                Operator.Right -> {
                    // 遇到右括号，持续弹出运算符，直到遇到左括号
                    while (operationStack.peek() != Operator.Left) {
                        deque.offerLast(operationStack.pop())
                    }
                    // 弹出左括号
                    operationStack.pop()
                }
                else -> {
                    // 如果栈不为空，栈顶不是左括号，栈顶运算符的优先级大于等于当前运算符
                    // 将栈内的运算符弹出到队列，直到不满足前面的条件
                    while (!operationStack.isEmpty() && operationStack.peek() != Operator.Left
                            && any.priority <= operationStack.peek().priority) {
                        deque.offerLast(operationStack.pop())
                    }
                    // 不满足上述条件，将运算符压入栈内
                    operationStack.push(any)
                }
            }
        }
    }
    // 将剩余的运算符全部弹出
    while (!operationStack.isEmpty()) {
        deque.offerLast(operationStack.pop())
    }
    return deque
}

/**
 * 根据后缀表达式计算结果。要求序列中所有的数为Int
 */
fun calculateReversePolishNotation(expressionQueue: Queue<Any>): Int {
    val calculateStack: Stack<Int> = Stack()
    var obj: Any?
    while (expressionQueue.poll().also { obj = it } != null) {
        if (obj is Int) {
            calculateStack.push(obj as Int)
        } else if (obj is Operator) {
            val numberOne = calculateStack.pop()
            val numberTwo = calculateStack.pop()
            calculateStack.push(calculate(numberOne, numberTwo, obj as Operator))
        }
    }
    // 弹出运算结果
    return calculateStack.pop()
}

/**
 * 根据操作符计算结果
 * @param numberOne 操作数
 * @param numberTwo 被操作数(被除数)
 */
fun calculate(numberOne: Int,
              numberTwo: Int, operator: Operator): Int {
    return when(operator) {
        Operator.Plus -> {
            numberTwo + numberOne
        }
        Operator.Minus -> {
            numberTwo - numberOne
        }
        Operator.Multiply -> {
            numberTwo * numberOne
        }
        Operator.Divide -> {
            numberTwo / numberOne
        }
        else -> 1
    }
}