转移价值？还是 策略？ 一个可转移的连续强化学习的中心框架

TRANSFER VALUE OR POLICY? A AVALUE-CENTRIC FRAMEWORK TOWARDS TRANSFERRABLE CONTINUOUS REINFORCEMENT LEARNING

ABSTRACT

Transferring learned knowledge from one environment to another is an important step towards practical reinforcement learning (RL). In this paper, we investigate the problem of transfer learning across environments with different dynamics while accomplishing the same task in the continuous control domain. We start by illustrating the limitations of policy-centric methods (policy gradient, actor-critic, etc.) when transferring knowledge across environments. We then propose a general model-based value-centric (MVC) framework for continuous RL. MVC learns a dynamics approximator and a value approximator simultaneously in the source domain, and makes decision based on both of them. We evaluate MVC against popular baselines on 5 benchmark control tasks in a training from scratch setting and a transfer learning setting. Our experiments demonstrate MVC achieves comparable performance with the baselines when it is trained from scratch, while it significantly surpasses them when it is used in the transfer setting.
将学到的知识从一个环境转移到另一个环境是实践强化学习（RL）的重要一步。在本文中，我们研究了在不同动态的环境中进行转移学习的问题，同时在连续控制域中完成相同的任务。我们首先阐述了在跨环境传递知识时以政策为中心的方法（政策梯度，行为者 - 评论家等）的局限性。然后，我们为连续RL提出了一个基于模型的通用的以价值为中心（MVC）的框架。 MVC在源域中同时学习动态近似值和值近似值，并基于它们做出决策。我们在5个基准控制任务中针对流行基线评估MVC，从头开始设置培训和转移学习设置。我们的实验表明，当从头开始训练时，MVC可以获得与基线相当的性能，而当它用于传输设置时，它显着超过它们。

1INTRODUCTION

While the achievements of deep reinforcement learning (DRL) are exciting in having conquored many computer games (Go (Silver et al., 2016; 2017), Atari games (Mnih et al., 2015)), in practice, it is still hard for these algorithms to find applications in real-world environments. Among the impediments, a primary obstacle is that they could fail even if the environment to deploy the agent is slightly different from where they were trained (Tan et al., 2018; Bousmalis et al., 2018; Tobin et al., 2017; Tamar et al., 2016). In other words, they lack the desired ability to transfer experiences learned from one environment to another. These observations motivate us to ask, (1) why are current RL algorithms so inefficient in transfer learning and (2) what kind of RL algorithms could be friendly to transfer learning by nature?

In this work, we explore the two questions and present a partial answer based on analysis and experiments. Our exploration concentrates on control tasks due to its broad impact; in particular, we further assume that across environments only their dynamics are not the same. Possible sources of such dynamics discrepancy could be variation of physical properties such as object mass, gravity, and surface friction. It is worth noting that our framework is general and we do not assume any specific perturbation source or type.

Our investigation starts with understanding the limitation of transferring the policy function (which maps a state to a distribution of actions) across environments. We analyze this transfer strategy because the de facto DRL framework in the control domain (DDPG (Lillicrap et al., 2015), TRPO (Schulman et al., 2015), A3C (Mnih et al., 2016), etc.) are policy-centric methods, which directly optimize the policy function. As a result, these methods learn a precise policy function, and sometimes also produce an imprecise value/Q-function as a side product. However, even if a perfect policy function has been learned from the source environment, this policy could behave quite poorly, or even fail, in the new environment, especially when the action space is hard-constrained (e.g., force or torque usually has a maximal value). We illustrate this by a simple example: Imagine a child shooting three-pointers when playing basketball. With a 600g ball, she can make the three-pointer. However, she may hardly make the three with a 800g ball because it is too heavy. What will she do? Most likely she will step forward, approach the basket, and make a closer jump-shot. We see that marginal dynamics variation can lead to drastic policy change, and direct policy optimization initialized from the old policy would not be efficient. We will analyze this issue more systematically by theoretical and experimental approaches throughout the paper.
虽然深度强化学习（DRL）的成就令人兴奋，但已经征服了许多电脑游戏（Go（Silver et al。，2016; 2017），Atari游戏（Mnih et al。，2015）），在实践中，它仍然很难这些算法可以在真实环境中查找应用程序。在这些障碍中，一个主要障碍是，即使部署代理的环境与他们接受培训的环境略有不同，他们也可能失败（Tan等，2018; Bousmalis等，2018; Tobin等，2017; Tamar等，2016）。换句话说，他们缺乏将从一个环境学到的经验转移到另一个环境的理想能力。这些观察激励我们提出这样的问题：（1）为什么当前的RL算法在转移学习中效率低下;（2）哪种RL算法可以友好地转移学习本质？

在这项工作中，我们探讨了两个问题，并基于分析和实验提出了部分答案。由于其广泛的影响，我们的探索集中在控制任务上;特别是，我们进一步假设在整个环境中，只有它们的动态不同。这种动态差异的可能来源可能是物理性质的变化，例如物体质量，重力和表面摩擦。值得注意的是，我们的框架是通用的，我们不承担任何特定的扰动源或类型。

我们的调查首先要了解跨环境转移策略功能（将状态映射到动作分布）的限制。我们分析了这种转移策略，因为控制域中的事实上的DRL框架（DDPG（Lillicrap等，2015），TRPO（Schulman等，2015），A3C（Mnih等，2016）等）是以政策为中心的方法，直接优化政策功能。结果，这些方法学习了精确的策略功能，并且有时还产生不精确的值/ Q函数作为副产品。然而，即使从源环境中学习了完美的策略功能，该策略在新环境中也可能表现得很差甚至失败，尤其是当动作空间受到严格限制时（例如，力或扭矩通常具有最大值）。我们通过一个简单的例子来说明这一点：想象一下孩子在打篮球时投中三分球。凭借600克球，她可以制造三分球。然而，由于太重，她可能很难用800克球制作三个球。她会做什么？最有可能的是，她会向前迈进，接近篮筐，然后进行更近距离的跳投。我们看到边际动态变化可能导致政策的剧烈变化，而从旧政策初始化的直接政策优化效率不高。我们将在整篇论文中通过理论和实验方法更系统地分析这个问题。

The investigation implies that, instead of directly transferring policies, the swift transfer should be grounded in richer and more structured knowledge of the task, so as to facilitate the judgment of whether the agent is approaching the goal, which is critical for making the right decision. Enlightened by the above intuition, we propose a simple model-based and value-centric framework for continuous reinforcement learning.

Our method contains two disentangled components: a dynamics approximator (model-based) and a state value function approximator (value-centric). The agent plans its action by solving an opti-mization problem using both approximators. As side products, this design learns a precise transition function, a precise reward function, and a precise value function on a subset of states. In particular, knowledge from historical explorations have been stored in the value function. In comparison, previous policy-centric methods can only produce a precise policy function, thus our framework allows to transfer much more information. By fine-tuning the whole framework in a new environment, our agent can adapt quickly with much lower sample complexity than state-of-the-art.

We call our method value-centric because it strives to learn a precise value function. The general framework is inspired from the Value Iteration (VI) method, which is a classical approach for discrete decision making. However, since control problems have a continuous action space, we cannot directly enumerate over the action space as in the discrete setting but have to address the highly non-convex optimization problem. To make it tractable, we leverage differentiable function approximators like neural networks to learn the dynamics and the value function. By such an approximation, it is possible to solve the optimization problem with state-of-the-art optimizers effectively.

We also theoretically analyze our value-centric framework and classical policy gradient algorithms from an optimization perspective. To build an intuitive understanding, we create a simple and illustrative example that clearly shows a local optimum in the policy space can prevent policy gradient methods from transferring successfully, but will not affect our value-centric framework.

We summarize our contributions as below:
We provide a theoretical justification to show the advantage of value-centric methods from an optimization perspective.

We propose a novel value-centric framework for continuous reinforcement learning of comparable sample efficiency with popular deep RL methods in the training from scratch setting.

Extensive experiments show the superiority of our method in a transfer learning setting
调查意味着，快速转移不应直接转移政策，而应以更丰富，更有条理的任务知识为基础，以便判断代理人是否接近目标，这对做出正确决策至关重要。 。在上述直觉的启发下，我们提出了一个简单的基于模型和价值为中心的框架，用于持续强化学习。

我们的方法包含两个解缠绕的组件：动态近似器（基于模型）和状态值函数逼近器（以值为中心）。代理通过使用两个逼近器解决优化问题来计划其行为。作为副产品，该设计在状态子集上学习精确的过渡函数，精确的奖励函数和精确的值函数。特别是，历史探索中的知识已存储在价值函数中。相比之下，以前以策略为中心的方法只能生成精确的策略函数，因此我们的框架允许传输更多信息。通过在新环境中微调整个框架，我们的代理可以快速适应，比最先进的样本复杂得多。

我们称我们的方法以价值为中心，因为它努力学习精确的价值函数。总体框架的灵感来自于价值迭代（VI）方法，这是一种用于离散决策的经典方法。但是，由于控制问题具有连续的动作空间，我们不能像在离散设置中那样直接枚举动作空间，而是必须解决高度非凸优化问题。为了使其易于处理，我们利用像神经网络这样的可微函数逼近器来学习动力学和价值函数。通过这种近似，可以有效地利用现有技术的优化器来解决优化问题。

我们还从理论上分析了我们以价值为中心的框架和经典的政策梯度算法。为了建立直观的理解，我们创建了一个简单的说明性示例，清楚地显示了策略空间中的局部最优可以阻止策略梯度方法成功传输，但不会影响我们以价值为中心的框架。

我们总结了以下贡献：
我们提供理论上的理由，从优化的角度展示以价值为中心的方法的优势。

我们提出了一种新的以价值为中心的框架，用于在从头开始的训练中使用流行的深度RL方法进行可比较的样本效率的连续强化学习。

大量实验表明我们的方法在转移学习环境中的优越性

2 BACKGROUND

2.1 MDPS AND NOTATION

Low-dimensional Assumption We focus on control problems which usually have well-engineered and low-dimensional state/action representations. Not rigorously, the assumption has two implica-tions:

• Property 1: For a smooth function f(at) over A, we can find its approximate solution by sampling over the domain and optimizing locally;

• Property 2: We can learn a network to approximate the transition and reward functions.

Empirically, we find evidence of both properties as in our experiment section (Sec 6).
低维度假设我们专注于通常具有精心设计和低维度状态/动作表示的控制问题。 不严格，这个假设有两个含义：

• 属性1：对于A上的平滑函数f（at），我们可以通过对域进行采样并在本地优化来找到其近似解;

• 属性2：我们可以学习网络来近似过渡和奖励功能。

根据经验，我们在实验部分（第6节）中找到了两种性质的证据。

2.2 TRANSFER LEARNING

Many differently posed transfer learning problems have been discussed in the reinforcement learning literature (Taylor & Stone, 2009). In this work, we study the problem of the environment slightly changing while the task remains the same. For example, in the pendulum swing-up problem, once the agent learns how to swing up a 1kg pendulum, we expect that it could quickly adapt itself to swing up a 2kg pendulum leveraging the learned knowledge. We formulate our setting by modifying the aforementioned standard RL setting. We consider a pair of MDPs sharing state and action spaces. Their transition dynamics T and reward functions R are parameterized by a vector :
在强化学习文献中已经讨论了许多不同的转移学习问题（Taylor＆Stone，2009）。 在这项工作中，我们研究环境问题略有变化，同时任务保持不变。 例如，在钟摆摆动问题中，一旦经纪人学会如何摆动1千克钟摆，我们就可以期待它可以快速适应自身以利用学到的知识摆动2千克钟摆。 我们通过修改上述标准RL设置来制定我们的设置。 我们考虑一对共享状态和动作空间的MDP。 它们的过渡动力学T和奖励函数R由向量参数化：

3WHY TRANFERRING POLICY CAN BE DIFFICULT? A SIMPLE ILLUSTRATION

In the RL community, most control tasks are solved by policy gradient-based methods. In this section, we illustrate the limitation of transferring policy by a simple example and compare it with a value-centric method.
在RL社区中，大多数控制任务通过基于策略梯度的方法来解决。 在本节中，我们通过一个简单的例子来说明转移政策的局限性，并将其与以价值为中心的方法进行比较。

Now we show the different behaviors of the value-and policy-centric strategies in a transfer learning setting. For the source environment, f1 = 0.7 and f2 = 0.8. It is not hard to find that the optimal path is path1. Then we modify the transition rule of the environment by slightly varying f1 and f2. We set f1 = 0.8 and f2 = 0.7. While the variation of the environment is relatively small,the optimal policy for s0 is completely different and has changed to path2. The optimal state value function and policy are shown in Table 1 in the Appendix B.

To compare policy- and value-centric strategies, we run two representative algorithms on this game – the Policy Gradient (PG) algorithm (Williams, 1992) (policy-centric) and the Value Iteration (VI) algorithm (Sutton et al., 1998) (value-centric). We assume the value-centric methods have access
现在我们在转移学习环境中展示价值和政策中心策略的不同行为。 对于源环境，f1 = 0.7，f2 = 0.8。 发现最佳路径是path1并不难。 然后我们通过稍微改变f1和f2来修改环境的转换规则。 我们设置f1 = 0.8和f2 = 0.7。 虽然环境的变化相对较小，但s0的最优策略完全不同，并且已经变为path2。 最佳状态值函数和策略如附录B中的表1所示。

为了比较政策和价值为中心的策略，我们在这个游戏上运行两个代表性的算法 - 政策梯度（PG）算法（Williams，1992）（以政策为中心）和价值迭代（VI）算法（Sutton等， 1998）（以价值为中心）。 我们假设以价值为中心的方法具有访问权限

4MODEL-BASED AND VALUE-CENTRIC (MVC) REINFORCEMENT LEARNING

4.1 VALUE-CENTRIC METHOD IN TRANSFER LEARNING

Our objective is to make the agent learn faster in a new environment after trained in a similar environment. From the above discussion, we know that instead of directly transferring policies, the swift transfer should be grounded in richer and more structured knowledge of the task. It is worth exploring transfer by value function since the value function contains more information than the policy alone. A straight-forward idea is to utilize the value/Q function from actor-critic algorithms such as DDPG to facilitate transfer learning. However, the value/Q function learned from the actor-critic algorithm is usually imprecise, and it does not capture so much knowledge in the original environment. To address this issue, we propose an algorithm to directly train a precise value function in the original environment. We call it a value-centric method. Then, we just need to fine-tune this value function to help the agent adapt to the new environment. In the following subsections, we explain how to train this precise value function from scratch.
我们的目标是在经过类似环境培训后，让代理在新环境中学得更快。从上面的讨论中，我们知道，快速转移应该建立在更丰富，更有条理的任务知识之上，而不是直接转移政策。值得探索按值传递函数，因为值函数包含的信息多于单独的策略。一个直截了当的想法是利用演员评论算法（如DDPG）的值/ Q函数来促进转移学习。然而，从actor-critic算法中学习的值/ Q函数通常是不精确的，并且它在原始环境中没有捕获如此多的知识。为了解决这个问题，我们提出了一种算法来直接训练原始环境中的精确值函数。我们称之为以价值为中心的方法。然后，我们只需要微调这个值函数，以帮助代理适应新环境。在以下小节中，我们将解释如何从头开始训练这个精确的值函数。

CONTINUOUS VALUE ITERATION

To better explain our main algorithm, we first propose a Continuous Value Iteration algorithm, which is possible to make use of Property 1 in Sec 2.1 to build a value-centric method. Theorem 2 in the Appendix suggests it always converges.
为了更好地解释我们的主算法，我们首先提出了一种连续值迭代算法，该算法可以利用第2.1节中的属性1来构建以价值为中心的方法。 附录中的定理2表明它总是收敛。

4.3 ALGORITHM

Due to the superior parallel computing ability of modern GPUs, the optimization with different initial seeds can be operated simultaneously so that additional time consumption is limited. For exploration purpose, we also add noise (e.g. Ornstein-Uhlenbeck process) to the optimal action. While it is possible to expand the r.h.s. to a multi-step planning, notoriously, a learned model is inclined to diverge in long-horizon predictions. Consequently, we only use the one-step version for policy search.

To approximate the value function, we update the value approximator by the supervision of temporal-difference error (TD-error). Since updating the value function across the whole state space is unrealistic, we update the value approximator only by the data sampled from the environment in the
由于现代GPU具有优越的并行计算能力，可以同时操作具有不同初始种子的优化，从而限制额外的时间消耗。 出于探索目的，我们还将噪声（例如Ornstein-Uhlenbeck过程）添加到最佳动作中。 虽然可以扩展r.h.s.s. 众所周知，对于多步计划，学习模型倾向于在长期预测中发散。 因此，我们仅使用一步版本进行策略搜索。

为了近似值函数，我们通过监视时差误差（TD误差）来更新值近似值。 由于在整个状态空间中更新值函数是不现实的，因此我们仅通过从环境中采样的数据更新值近似值。

Online training makes the whole framework more light-weight while sacrificing the guarantee of convergence. One can improve the training paradigm with past experience from the replay buffer or advanced sampling skills on the state space, but we leave them as future work.

Like DDPG, we employ a target network parameterized by to stabilize the training. To speed up computation, we also fork multiple agents to run in parallel and synchronize them by a global agent. Algotihm 1 recaptures the whole algorithm paradigm.
在线培训使整个框架更轻量化，同时牺牲了融合的保证。 人们可以通过重置缓冲区的过去经验或州空间的高级抽样技能来改进训练范例，但我们将它们留作未来的工作。

与DDPG一样，我们采用参数化的目标网络来稳定培训。 为了加快计算速度，我们还将多个代理程序分叉并行运行，并通过全局代理程序对它们进行同步。 Algotihm 1重新捕获了整个算法范例。

5A THEORETICAL JUSTIFICATION FROM THE OPTIMIZATION PERSPECTIVE

We will show the limitation of policy-centric methods and the nice properties of value-centric method. We narrow the analysis of policy-centric frameworks down to the landscape of J( ). To save space, we leave the theorems and detailed proofs in Appendix A. We explain the intuitions here:

First, we show in Theorem 1 that, for an arbitrary MDP with a deterministic transition function, a local optimum of J( ) that traps gradient-based methods could exist under a weak condition. In fact, the local optimum issue is introduced by the parameterization of ’s output space, e.g., a Gaussian distribution. If we allow to be an arbitrary distribution, the local optimum will vanish (Proposition 1). The example in Sec 3 exactly shows a failure case of transferring policy due to a local optimum.

Second, we show in Theorem 2 that, for the same type of MDPs, the Continuous Value Iteration algorithm leveraging Property 1 in Sec 2.1 can share the favorable converge property of classical value iteration. That is, the distance between a current value function and the optimal value function will be squeezed at linear rate, thus it always converges. In addition, Proposition 2 implies that a small perturbation to the environment is only likely to cause a marginal change to the optimal value function; therefore, the old value function would serve as a good initialization point.
我们将展示以政策为中心的方法的局限性和以价值为中心的方法的优良特性。我们将以政策为中心的框架的分析缩小到J（）的格局。为了节省空间，我们将定理和详细证明留在附录A中。我们在此解释直觉：

首先，我们在定理1中表明，对于具有确定性转移函数的任意MDP，陷阱基于梯度的方法的局部最优J（）可能存在于弱条件下。实际上，局部最优问题是通过输出空间的参数化引入的，例如高斯分布。如果我们允许任意分布，局部最优将消失（命题1）。第3节中的示例确切地显示了由于局部最优而转移策略的失败情况。

其次，我们在定理2中表明，对于相同类型的MDP，利用2.1节中的属性1的连续值迭代算法可以共享经典值迭代的有利收敛性。也就是说，当前值函数和最佳值函数之间的距离将以线性速率被挤压，因此它总是收敛。此外，命题2意味着对环境的微小扰动只会导致最优值函数的边际变化;因此，旧的值函数将作为一个良好的初始化点。

6 EXPERIMENTS

We first compare our value-centric method against the policy gradient baselines in the training from scratch setting. We also show that our value-centric method beats baselines in the transfer learning setting. Finally, we conduct ablation study over method parameters and diagnose the components.
我们首先将我们以价值为中心的方法与从头开始设置的培训中的政策梯度基线进行比较。 我们还表明，我们以价值为中心的方法在转移学习环境中胜过基线。 最后，我们对方法参数进行消融研究并诊断组件。

6.1 SETUP

We evaluate our algorithm and two prevalent continuous RL methods, Deep Deterministic Policy Gradient (DDPG) (Lillicrap et al., 2015) and Trust Region Policy Optimization (TRPO) (Schulman et al., 2015), on five control tasks in the OpenAI Gym (Brockman et al., 2016):HalfCheetah-v1,InvertedPendulum-v1, InvertedDoublePendulum-v1, Pendulum-v0, and Reacher-v1. For baselines, we use the code from OpenAI Baselines (Dhariwal et al., 2017) and fine-tuned their hyper-parameters as much as we can. More details can be found in the Appendix D.
我们评估了我们的算法和两种流行的连续RL方法，深度确定性政策梯度（DDPG）（Lillicrap等，2015）和信任区域政策优化（TRPO）（Schulman等，2015），关于OpenAI中的五项控制任务 Gym（Brockman et al。，2016）：HalfCheetah-v1，InvertedPendulum-v1，InvertedDoublePendulum-v1，Pendulum-v0和Reacher-v1。 对于基线，我们使用OpenAI Baselines的代码（Dhariwal等，2017），并尽可能多地微调其超参数。 更多细节可以在附录D中找到。

6.2 MAIN RESULTS

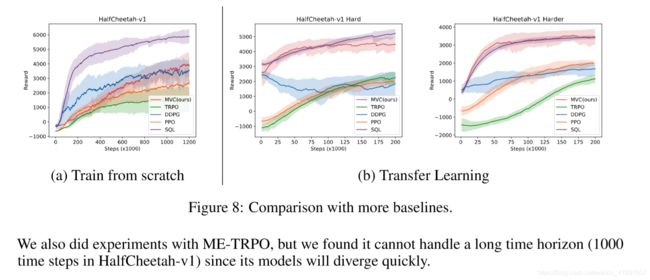
We compare the sample complexity and the performance of the three algorithms (MVC, DDPG, and TRPO) on the aforementioned five environments, for both the training from scratch setting and transfer learning setting. We also compare with PPO (Schulman et al., 2017) and SQL (Haarnoja et al., 2017) on HalfCheetah and show the results in Appendix F.

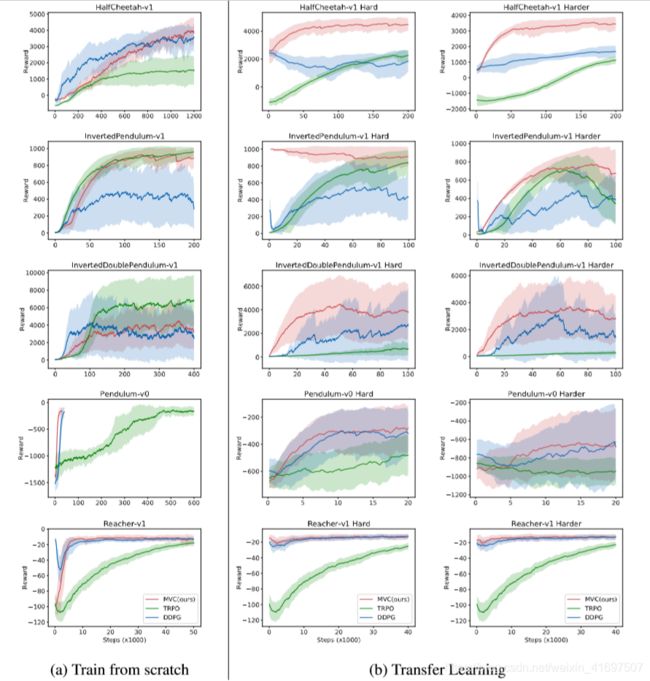
Train from Scratch The reported results (Fig. 8(a)) show the mean and standard deviation of 3 runs with different random seeds. In four of the environments (InvertedPendulum-v1, HalfCheetah-v1, Pendulum-v0, Reacher-v1), our method achieves comparable performance as the better baseline. In InvertedDoublePendulum-v1, though there is a significant gap between MVC and TRPO, MVC performs at the same level with DDPG.

Transfer across environments We demonstrate the superiority of our method when transferring across environments. For each of the above five environments, we change one or several physical properties, like the mass of pendulum, to create two new environments with novel dynamics. In one of the new environments, the change is relatively small (we call it ’Hard’ in the plot), while the other is more intensively perturbed (we call it ’Harder’ in the plot). We first train standard agents on the original environment. For fair comparison, we pick the agents that achieve comparable performance for all methods in the original environment. Please refer to Appendix D for the details of the modification and the agents. To avoid the possibility of under-exploration in the new environments, we reset the exploration noise of all the algorithms. We directly fine-tune all the agents with the same number of simulation steps. The results are shown in Fig. 8(b).

On all the environments, we observed that TRPO has the worst overall transfer performance. DDPG and MVC have similar transferrability on simple tasks like Reacher-v1 and Pendulum-v0. However, on more complicated tasks like HalfCheetah-v1,the performance of DDPG is significantly worse than MVC. Further investigation shows that DDPG can actually learn a high-quality Q function for simple environments, which serves a similar role as our value function. However, on more challenging games such as HalfCheetah-v1 and InvertedDoublePendulum-v1, as a policy-centric algorithm, the learned Q function is far from the true one (Fig. 7 in Appendix E), thus the transfer is significantly slower. The success and failure of DDPG again shows the central role value plays in transfer learning.
我们比较了上述五种环境下的三种算法（MVC，DDPG和TRPO）的样本复杂性和性能，从头开始设置训练和转移学习设置。我们还在HalfCheetah上与PPO（Schulman等，2017）和SQL（Haarnoja等，2017）进行比较，并在附录F中显示结果。

从Scratch训练报告的结果（图8（a））显示了不同随机种子的3次运行的平均值和标准差。在四个环境中（InvertedPendulum-v1，HalfCheetah-v1，Pendulum-v0，Reacher-v1），我们的方法实现了与更好的基线相当的性能。在InvertedDoublePendulum-v1中，尽管MVC和TRPO之间存在显着差距，但MVC与DDPG在同一级别上执行。

跨环境传输我们证明了在跨环境传输时我们的方法的优越性。对于上述五种环境中的每一种，我们都会改变一个或多个物理属性，如摆锤的质量，以创建两个具有新颖动态的新环境。在其中一个新环境中，变化相对较小（我们在图中称之为“硬”），而另一个则更加强烈地被扰动（我们在图中称之为“更难”）。我们首先在原始环境中培训标准代理。为了公平比较，我们选择在原始环境中为所有方法实现可比性能的代理。有关修改和代理的详细信息，请参阅附录D.为了避免在新环境中探索不足的可能性，我们重置了所有算法的探索噪声。我们使用相同数量的模拟步骤直接微调所有代理。结果如图8（b）所示。

在所有环境中，我们观察到TRPO具有最差的整体传输性能。 DDPG和MVC在简单任务（如Reacher-v1和Pendulum-v0）上具有类似的可传递性。但是，对于像HalfCheetah-v1这样的更复杂的任务，DDPG的性能明显比MVC差。进一步的研究表明，DDPG实际上可以为简单的环境学习高质量的Q函数，它具有与我们的价值函数类似的作用。然而，对于更具挑战性的游戏，例如HalfCheetah-v1和InvertedDoublePendulum-v1，作为一种以策略为中心的算法，学习的Q函数远非真实的（附录E中的图7），因此传输速度明显变慢。 DDPG的成功和失败再次表明了转移学习中的核心价值。

Figure 3: The training curves of training from scratch and transfer learning of MVC, TRPO, and DDPG. Thick lines correspond to mean episode rewards, and shaded regions show standard deviations of 3 random seeds. Our method (MVC) achieves comparable performance with the baselines while significantly outperforms them on transfer learning.

Note that, in HalfCheetah-v1-Harder, MVC achieves 3000 points in about 50k steps, while TRPO and DDPG only get around 1000 points after 200k steps.
图3：从头开始训练和MVC，TRPO和DDPG的转学习的训练曲线。 粗线对应于平均情节奖励，阴影区域显示3个随机种子的标准偏差。 我们的方法（MVC）实现了与基线相当的性能，同时在转移学习方面明显优于它们。

请注意，在HalfCheetah-v1-Harder中，MVC以大约50k步长达到3000点，而TRPO和DDPG仅在200k步后达到1000点。

6.3 ABLATION STUDY AND DIAGNOSIS OF COMPONENTS

Validation of Property1 Empirically, we find evidence for Property 1 and 2. Take HalfCheetah-v1 for example. For Property 1, we compare the optimization result of gradient-based method against random sampling with 106 points. Figure on the left demonstrates that Adam achieves comparable results with random sampling while being tens of times faster on our computer (a 48-core Xeon CPU with 2 Titan XP GPUs).

Validation for Property 2 Figure on the right shows that the loss functions for the transition network and reward network converge in less than 100k time steps, which means the transition network and reward network converges much faster than the value network (As shown in Fig. 8(a), the value network still does not converge after 1200k steps.). Therefore, selecting actions based on the learned transition network and reward network is trusty. We also observed that the learned transition and reward networks provide good start points for the training in the new environment.
Property1的验证根据经验，我们找到属性1和2的证据。以HalfCheetah-v1为例。 对于属性1，我们将基于梯度的方法的优化结果与具有106个点的随机采样进行比较。 左图显示Adam在随机采样时获得了可比较的结果，而在我们的计算机上速度提高了数十倍（一个48核Xeon CPU和2个Titan XP GPU）。

对属性2的验证图右侧显示转换网络和奖励网络的损失函数以不到100k的时间步长收敛，这意味着转换网络和奖励网络的收敛速度比价值网络快得多（如图8所示） （a），价值网络在1200k步之后仍然没有收敛。）。 因此，基于学习的转换网络和奖励网络选择动作是可信的。 我们还观察到，学习的过渡和奖励网络为新环境中的培训提供了良好的起点。

7RELATED WORK

Reinforcement Learning in Continuous Control Domain. Solving continuous control problems through reinforcement learning has been studied for decades (Sutton et al., 1998; Williams, 1992). Policy-based methods (Schulman et al., 2015; Mnih et al., 2016; Lillicrap et al., 2015) are more widely used. One exception is the NAF (Gu et al., 2016) method under the Q-learning framework which models the action space as a quadratic function.

Value-based Reinforcement Learning. The most relevant work in literature are perhaps the very recent Value Iteration Network (VIN) and Value Prediction Network (VPN) (Tamar et al., 2016; Oh et al., 2017). Though demonstrated better environment generalizability, VIN is specifically designed and only evaluated on the 2D navigation problem. VPN learns a dynamics model together with a value function and makes plans based on Monte Carlo tree search. In contrast to our work, VPN neither considered the continuous control problem nor thoroughly investigated their algorithm under the transfer learning setting.

Model-based Reinforcement Learning. For purposes such as increasing sample efficiency and designing smarter exploration strategies (e.g., curiosity-driven exploration), it can be beneficial to incorporate a learned dynamics model. Some very recent works have demonstrated the power of such model-based RL algorithms (Levine & Koltun, 2013; Nagabandi et al., 2017; Kurutach et al., 2018; Pathak et al., 2018; Feinberg et al., 2018; Pathak et al., 2017). However, to our knowledge, none of them has yet combined the value function with a learned dynamics model to solve continuous decision making problems.

Transfer Learning in Deep Reinforcement Learning. In this work, we study knowledge transfer problem across different MDPs.(Kansky et al., 2017) proposed the SchemaNetwork which learns the knowledge of the Atari physics engine by playing a standard version of the BreakOut game. (Higgins et al., 2017) learns disentangled representations in the source domains to achieve zero-shot domain adaption in the new environments. Finally, a straight-forward strategy is to show the agent all possible environments (Yu et al., 2017; Tan et al., 2018; Tobin et al., 2017).
连续控制领域的强化学习几十年来研究通过强化学习解决连续控制问题（Sutton等，1998; Williams，1992）。基于政策的方法（Schulman等，2015; Mnih等，2016; Lillicrap等，2015）被更广泛地使用。一个例外是Q-learning框架下的NAF（Gu et al。，2016）方法，该方法将动作空间建模为二次函数。

基于价值的强化学习文献中最相关的工作可能是最新的价值迭代网络（VIN）和价值预测网络（VPN）（Tamar等，2016; Oh等，2017）。虽然展示了更好的环境普遍性，但VIN是专门设计的，仅针对2D导航问题进行评估。 VPN学习动态模型和值函数，并根据蒙特卡罗树搜索制定计划。与我们的工作相比，VPN既没有考虑连续控制问题，也没有在转移学习设置下彻底调查他们的算法。

基于模型的强化学习为了提高样本效率和设计更智能的探索策略（例如，好奇心驱动的探索）等目的，结合学习动力学模型可能是有益的。一些最近的工作证明了这种基于模型的RL算法的能力（Levine＆Koltun，2013; Nagabandi等，2017; Kurutach等，2018; Pathak等，2018; Feinberg等，2018; Pathak等，2017）。然而，据我们所知，他们都没有将价值函数与学习动力学模型相结合来解决持续的决策问题。

深度强化学习中的转移学习在这项工作中，我们研究跨不同MDP的知识转移问题。（Kansky等，2017）提出了SchemaNetwork，它通过播放标准版本来学习Atari物理引擎的知识。 BreakOut游戏。 （Higgins等，2017）学习源域中的解开的表示，以在新环境中实现零射击域适应。最后，直接的策略是向代理显示所有可能的环境（Yu等人，2017; Tan等人，2018; Tobin等人，2017）。

REFERENCES

Mohammed Abbad and Jerzy A Filar. Perturbation and stability theory for markov control problems.

IEEE Transactions on Automatic Control, 37(9):1415–1420, 1992.

Konstantinos Bousmalis, Alex Irpan, Paul Wohlhart, Yunfei Bai, Matthew Kelcey, Mrinal Kalakrish-nan, Laura Downs, Julian Ibarz, Peter Pastor Sampedro, Kurt Konolige, et al. Using simulation and domain adaptation to improve efficiency of deep robotic grasping. arXiv: Learning, 2018.

Greg Brockman, Vicki Cheung, Ludwig Pettersson, Jonas Schneider, John Schulman, Jie Tang, and Wojciech Zaremba. Openai gym, 2016.

Prafulla Dhariwal, Christopher Hesse, Oleg Klimov, Alex Nichol, Matthias Plappert, Alec Radford, John Schulman, Szymon Sidor, Yuhuai Wu, and Peter Zhokhov. Openai baselines. https: //github.com/openai/baselines, 2017.

Vladimir Feinberg, Alvin Wan, Ion Stoica, Michael I. Jordan, Joseph E. Gonzalez, and Sergey Levine. Model-based value estimation for efficient model-free reinforcement learning. arXiv: Learning, 2018.

Shixiang Gu, Timothy P Lillicrap, Ilya Sutskever, and Sergey Levine. Continuous deep q-learning with model-based acceleration. international conference on machine learning, pp. 2829–2838, 2016.

Tuomas Haarnoja, Haoran Tang, Pieter Abbeel, and Sergey Levine. Reinforcement learning with deep energy-based policies. In International Conference on Machine Learning, pp. 1352–1361, 2017.

Irina Higgins, Arka Pal, Andrei A Rusu, Loic Matthey, Christopher P Burgess, Alexander Pritzel, Matthew M Botvinick, Charles Blundell, and Alexander Lerchner. Darla: Improving zero-shot transfer in reinforcement learning. international conference on machine learning, pp. 1480–1490, 2017.

Ken Kansky, Tom Silver, David A Mely, Mohamed Eldawy, Miguel Lazarogredilla, Xinghua Lou, Nimrod Dorfman, Szymon Sidor, D Scott Phoenix, and Dileep George. Schema networks: Zero-shot transfer with a generative causal model of intuitive physics. international conference on machine learning, pp. 1809–1818, 2017.

Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. international conference on learning representations, 2015.

Thanard Kurutach, Ignasi Clavera, Yan Duan, Aviv Tamar, and Pieter Abbeel. Model-ensemble trust-region policy optimization. international conference on learning representations, 2018.

Sergey Levine and Vladlen Koltun. Guided policy search. In International Conference on Machine Learning, pp. 1–9, 2013.

Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971, 2015.

Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A Rusu, Joel Veness, Marc G Bellemare, Alex Graves, Martin A Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al. Human-level control through deep reinforcement learning. Nature, 518(7540):529–533, 2015.

Volodymyr Mnih, Adria Puigdomenech Badia, Mehdi Mirza, Alex Graves, Timothy Lillicrap, Tim Harley, David Silver, and Koray Kavukcuoglu. Asynchronous methods for deep reinforcement learning. In International conference on machine learning, pp. 1928–1937, 2016.

Anusha Nagabandi, Gregory Kahn, Ronald S Fearing, and Sergey Levine. Neural network dynamics for model-based deep reinforcement learning with model-free fine-tuning. arXiv: Learning, 2017.

Junhyuk Oh, Satinder Singh, and Honglak Lee. Value prediction network. In Advances in Neural Information Processing Systems, pp. 6118–6128, 2017.

Deepak Pathak, Pulkit Agrawal, Alexei A Efros, and Trevor Darrell. Curiosity-driven exploration by self-supervised prediction. international conference on machine learning, pp. 2778–2787, 2017.

Deepak Pathak, Parsa Mahmoudieh, Michael Luo, Pulkit Agrawal, Dian Chen, Fred Shentu, Evan Shelhamer, Jitendra Malik, Alexei A Efros, and Trevor Darrell. Zero-shot visual imitation. international conference on learning representations, 2018.

John Schulman, Sergey Levine, Pieter Abbeel, Michael Jordan, and Philipp Moritz. Trust region policy optimization. In International Conference on Machine Learning, pp. 1889–1897, 2015.

John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347, 2017.

David Silver, Aja Huang, Chris J Maddison, Arthur Guez, Laurent Sifre, George Van Den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, et al. Mastering the game of go with deep neural networks and tree search. Nature, 529(7587):484–489, 2016.

David Silver, Julian Schrittwieser, Karen Simonyan, Ioannis Antonoglou, Aja Huang, Arthur Guez, Thomas Hubert, Lucas Baker, Matthew Lai, Adrian Bolton, et al. Mastering the game of go without human knowledge. Nature, 550(7676):354–359, 2017.

Richard S Sutton, Andrew G Barto, et al. Reinforcement learning: An introduction. MIT press, 1998.

Aviv Tamar, Yi Wu, Garrett Thomas, Sergey Levine, and Pieter Abbeel. Value iteration networks. In Advances in Neural Information Processing Systems, pp. 2154–2162, 2016.

Jie Tan, Tingnan Zhang, Erwin Coumans, Atil Iscen, Yunfei Bai, Danijar Hafner, Steven Bohez, and Vincent Vanhoucke. Sim-to-real: Learning agile locomotion for quadruped robots. robotics science and systems, 14, 2018.

Matthew E. Taylor and Peter Stone. Transfer learning for reinforcement learning domains: A survey.

Journal of Machine Learning Research, 10(10):1633–1685, 2009.

Joshua Tobin, Rachel Fong, Alex Ray, Jonas Schneider, Wojciech Zaremba, and Pieter Abbeel.

Domain randomization for transferring deep neural networks from simulation to the real world.

intelligent robots and systems, pp. 23–30, 2017.

Ronald J Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning, 8(3-4):229–256, 1992.

Wenhao Yu, Jie Tan, C Karen Liu, and Greg Turk. Preparing for the unknown: Learning a universal policy with online system identification. robotics science and systems, 13, 2017.

APPENDIX A PROOFS FOR THE THEOREMS

For mathematical rigor, we suppose the state space and the action space are both continuous in this section.
对于数学严谨性，我们假设状态空间和动作空间在本节中都是连续的。

A.1 PROPOSITION 1 AND PROOF

PROPOSITION 2 AND PROOF

This bound is rather loose, and it can only be a partial explanation of the experimental results. The changes of environment in our experiments are much larger than a ’perturbation’.
这种界限相当松散，只能是对实验结果的部分解释。 我们实验中环境的变化远大于“扰动”。

A.3 THEOREM 1 AND PROOF

The proof is a trivial extension of conventional value iteration.

Proof. We start the proof by showing the exact value of the bound B, then we demonstrate how we can deduce the conclusion from B. to simplify the proof, we use the following notations:
证明。 我们通过显示绑定B的确切值来开始证明，然后我们演示如何从B.推断出结论以简化证明，我们使用以下符号：

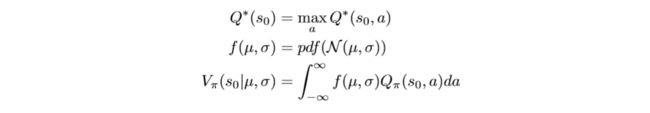
APPENDIX B DETAILS OF ILLUSTRATIVE EXAMPLE

We implement the MDP and the algorithms in MATLAB 2015b. For the policy gradient theorem, we use a variance-reduced version of the vanilla policy gradient:
我们在MATLAB 2015b中实现了MDP和算法。 对于策略梯度定理，我们使用vanilla政策梯度的方差减少版本：

APPENDIX C IMPLEMENTATION DETAILS

We use feed forward networks for all models and the activation function is ReLU. For transition network, reward network, and termination network, the networks have 2 hidden layers of size 512. For value network and target value network, the networks have 2 hidden layers of size 256 and 2 hidden layers of size 128. The weights of the networks are initialized by Xavier weight initializer. And the networks are all trained by Adam optimizer, the learning rates for transition network, reward network, termination network and value network are 1e-3, 1e-3, 1e-3, 1e-4, respectively.

The transition network, reward network, and termination network are trained 2 times for every 40 steps. The training data is uniformly sampled from the replay buffer, and the batch size is 512. The value network is trained 2 times in each step with the current (s, r, s0) tuple. At each time the value network is trained, the target networks will be soft updated as follows,
我们为所有模型使用前馈网络，激活功能是ReLU。 对于过渡网络，奖励网络和终端网络，网络有2个大小为512的隐藏层。对于价值网络和目标价值网络，网络有2个大小为256的隐藏层和2个大小为128的隐藏层。 网络由Xavier权重初始化器初始化。 并且网络都由Adam优化器训练，转换网络，奖励网络，终端网络和价值网络的学习率分别为1e-3,1e-3,1e-3,1e-4。

过渡网络，奖励网络和终止网络每40步训练2次。 从重放缓冲区统一采样训练数据，批量大小为512.每个步骤使用当前（s，r，s0）元组训练值网络2次。 在每次训练价值网络时，目标网络将软更新如下，

We use Adam optimizer with the learning rate of 0.1. To avoid trapped by local maxima, we set 200 initial points for the gradient descent procedure. When training from scratch, the optimizer will be called k times, where the initial value of k is 0 and it is increased by 1 for every 150k steps. The reason we do not optimize too many steps at the beginning is the value network is not accurate at that time. But when transferring, we set a fixed k = 10 because we have a good initialization for value network. After we get the action, a noise will be added to the action in order to encourage exploration. The noise we used is Ornstein-Uhlenbeck process with = 0 and = 0:15. And the noise will be decayed with the progress of training.

However, the above case is just for the tasks without true terminations. For the tasks with true terminations, i.e. the task will be terminated before reaching the time limit, the optimization needs to be re-writed as follows,
我们使用Adam优化器，学习率为0.1。 为了避免陷入局部最大值，我们为梯度下降过程设置了200个初始点。 从头开始训练时，优化器将被调用k次，其中k的初始值为0，并且每150k步长增加1。 我们一开始没有优化太多步骤的原因是价值网络在那时并不准确。 但是在转移时，我们设置了固定的k = 10，因为我们对价值网络进行了很好的初始化。 在我们采取行动后，将在行动中添加噪音以鼓励探索。 我们使用的噪声是Ornstein-Uhlenbeck过程，其中= 0和= 0:15。 随着训练的进展，噪音将会衰减。

但是，上述情况仅适用于没有真正终止的任务。 对于具有真正终止的任务，即任务将在达到时间限制之前终止，优化需要重新编写如下，

APPENDIX D EXPERIMENT DETAILS

Our simulation environment is OpenAI gym 0.9.3.

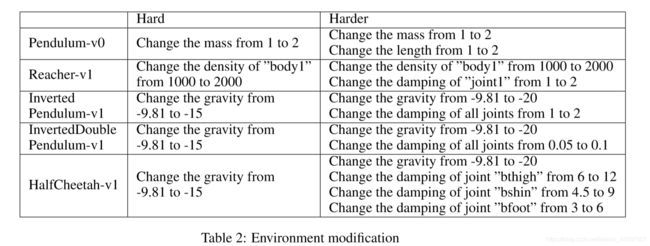
For transferring experiments, we change one or several physical properties in the environments. In one of the new environments,the change is relatively small (we call it ”Hard”), while the other is more intensively perturbed(we call it ”Harder”). We achieve it by directly modifying the codes or the XML files in the OpenAI gym library. The modifications are listed in the Table 2.
我们的模拟环境是OpenAI gym 0.9.3。

为了转移实验，我们在环境中更改一个或多个物理属性。 在其中一个新环境中，变化相对较小（我们称之为“硬”），而另一个则受到更强烈的干扰（我们称之为“更难”）。 我们通过直接修改OpenAI体育馆库中的代码或XML文件来实现它。 修改列于表2中。

In transferring experiments, we select the agents get similar scores in the original environment for fair comparison. Table 3 shows the scores of the agents we chose in different environments. To get these scores, we evaluate each agent 10 times and calculate the mean episode reward.
在转移实验时，我们选择代理在原始环境中获得相似的分数以进行公平比较。 表3显示了我们在不同环境中选择的代理商的分数。 为了得到这些分数，我们评估每个代理10次并计算平均情节奖励。

Figure 7: Density plot shows the estimated Q versus observed returns sampled from 5 test trajectories. for simple environments like Pendulum and Cartpole, the critic can predict the Q value quit accurate. However, in more complicated environment like Cheetah, the estimated Q are way more inaccurate. (This plot is from (Lillicrap et al., 2015))
图7：密度图显示了从5个测试轨迹中采样的估计Q值与观察到的回报。 对于像Pendulum和Cartpole这样的简单环境，评论家可以预测Q值准确无误。 然而，在像猎豹这样的更复杂的环境中，估计的Q更加不准确。 （该图来自（Lillicrap等，2015））

APPENDIX F SUPPLEMENTARY EXPERIMENT RESULTS

We compare the sample complexity and the performance of the five algorithms (MVC, DDPG, TRPO, PPO, and SQL) on the HalfCheetah, for both the training from scratch setting and transfer learning setting.

SQL is a continuous variant of Q-learning, which expresses the optimal policy via a Boltzmann distribution. PPO is developed from TRPO with several modifications. In the train from scratch setting, SQL shows the best sample efficiency (significantly better than other algorithms). This is probably because it improves exploration by incorporating an entropy term but all the other algorithms do not. However, in the transfer learning setting, the performance of MVC is nearly the same as SQL. As both are value-centric algorithms, we think the benefit of MVC comes from using an environment dynamics approximator. PPO shows better performance than TRPO (both in the train from scratch and the transfer learning), but still much worse than MVC.
我们比较了HalfCheetah上的五种算法（MVC，DDPG，TRPO，PPO和SQL）的样本复杂性和性能，以便从头开始设置培训和转移学习设置。

SQL是Q学习的连续变体，它通过Boltzmann分布表达最优策略。 PPO是从TRPO开发的，经过多次修改。 在从头开始设置的训练中，SQL显示了最佳的样本效率（明显优于其他算法）。 这可能是因为它通过合并熵项来改进探索，但所有其他算法都没有。 但是，在传输学习设置中，MVC的性能几乎与SQL相同。 由于两者都是以价值为中心的算法，我们认为MVC的好处来自于使用环境动态近似器。 PPO表现出比TRPO更好的性能（从头开始和转移学习），但仍然比MVC差。