Java优先队列

一、优先队列

优先队列应用场景：

  在一堆杂乱无序的数据里，尤其是当数据量特别大时，要选出最大（最小）的几个元素，那么就不必将所有数据都排序后再选择。这时需要一种合适的数据结构，能够删除最小元素和插入元素。

例如在一个有100万个数字的文件中选出最大的10个，百万整数文档链接

public static void main(String[] args) {
		//创建一个MinPQ实例，可以存放输入的最大的10个整数
        //MinPQ类的代码在下方会有介绍
        MinPQ pq = new MinPQ(10);

        //读取文件里的整数放入数组
		int[] a = In.readInts(args[0]);
		
        
        for(int i =0;i10)
				pq.delMin();
		}

        //将pq中存放的最大的10个数字放入一个栈中
		Stack stack = new Stack();
		while(!pq.isEmpty()) {
			stack.push(pq.delMin());
		}
        
        //输出栈中的数字
		for(Integer i:stack) {
			System.out.print(i+" ");
		}
	}

MinPQ的API

Class MinPQ>
MinPQ()         MinPQ(int max)	类初始化
void insert(Key key)	插入元素
Key min()	返回最小值
Key delMin()	删除最小值并返回
boolean isEmpty()	返回是否为空
int size()	返回优先队列中元素个数

insert 方法

 //插入元素
	public void insert(Key key) {
        //当元素个数等于pq数组末尾索引时，将pq数组长度翻倍（通过resize方法）
		if(n==pq.length-1) resize(2*pq.length);
		
        //将插入的元素放在数组末尾，然后通过上浮实现堆有序化
        pq[++n] = key;
		swim(n);
	}

什么​​​​​​是堆，

堆可以通过上浮和下沉实现堆的有序化。

堆上浮swim的代码

   //上浮指定位点，实现堆有序化
	public void swim(int k) {
		while(k>1&&less(k,k/2)) {
			exch(k,k/2);
			k/=2;
		}	
	}

堆下沉sink的代码

	public void sink(int k) {
		while(2*k<=n) {
			int j = 2*k;
			if(j

min返回最小值方法

    //返回最小值
	public Key min() {
		return pq[1];
	}

delMin删除最小值方法 

//删除最小值并返回
	public Key delMin() {
		Key min = pq[1];

        //交换堆顶与末尾的元素位置，然后将置换后的堆顶元素下沉
		exch(1,n--);
		pq[n+1] = null; //防止元素游离
		sink(1);       //下沉元素
		if(n<=(pq.length-1)/4) resize(pq.length/2); //当删除最小元素pq数组元素数量远小于数组长度时，将数组长度减半
		return min;
	}

isEmpty、size方法 

	public int size() {return n;}
	public boolean isEmpty() {return n==0;}

全源代码如下 

public class MinPQ>{
	private Key[] pq;
	private int n;
	
    //初始化
	MinPQ(){}
	
	MinPQ(int max){
		pq = (Key[]) new Comparable[max+1];
		n = 0;
	}

    //插入元素
	public void insert(Key key) {
        //当元素个数等于pq数组末尾索引时，将pq数组长度翻倍（通过resize方法）
		if(n==pq.length-1) resize(2*pq.length);
		
        //将插入的元素放在数组末尾，然后通过上浮实现堆有序化
        pq[++n] = key;
		swim(n);
	}
    
    //resize函数，改变数组长度
	private void resize(int max) {
		Key[] temp = (Key[]) new Comparable[max];
		for(int i =1;i<=n;i++) {
			temp[i] = pq[i];
		}
		pq = temp;
	}

    //返回最小值
	public Key min() {
		return pq[1];
	}

    //删除最小值并返回
	public Key delMin() {
		Key min = pq[1];

        //交换堆顶与末尾的元素位置，然后将置换后的堆顶元素下沉
		exch(1,n--);
		pq[n+1] = null; //防止元素游离
		sink(1);       //下沉元素
		if(n<=(pq.length-1)/4) resize(pq.length/2); //当删除最小元素pq数组元素数量远小于数组长度时，将数组长度减半
		return min;
	}

    //上浮指定位点，实现堆有序化
	public void swim(int k) {
		while(k>1&&less(k,k/2)) {
			exch(k,k/2);
			k/=2;
		}
		
	}

    //下沉元素实现堆有序
	public void sink(int k) {
		while(2*k<=n) {
			int j = 2*k;
			if(j

二、索引优先队列

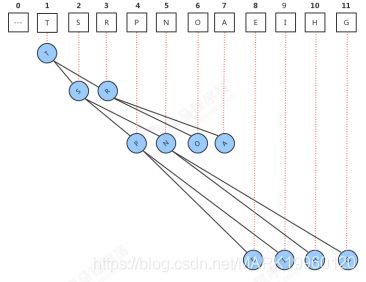
        由上可知优先队列的数据结构其实是数组，通过改变数组的顺序实现堆有序，从而实现优先队列；但是原始数据数组的顺序被打乱了。如果原始数据数组排序很重要，需要保留原始数据的数组索引该怎么办呢？这时就要用到索引优先队列 IndexMinPQ

        例：下表数组索引代表学生学号，数组内容代表考试成绩(100分满分),对成绩排序时，需要保留学生学号(即原数组索引)，

内容	56	78	93	87	42	65	86	...
索引	0	1	2	3	4	5	6	...

先看IndexMinPQ的API

IndexMin(int maxN)	创建一个最大容量为maxN的索引优先队列
void insert(int k, Item item)	插入元素及其索引
void change(int k ,Item item)	改变索引k的元素
boolean contains(int k)	是否包含索引为k的元素
void delete(int k)	删除索引k及其相关联的元素
Item min()	返回最小元素
int minIndex()	返回最小元素索引
int delMin()	删除最小元素并返回索引
boolean isEmpty()	该索引优先队列是否为空
int size()	索引优先队列的大小

        实现索引优先队列很简单，只需在优先队列的基础上加上一个索引数组就行，在原数组上改变元素位置实现堆有序

优先队列只需原始数据的数组即可

 

         要保留原始数组的索引，只需添加一个整数型数组储存原始数组索引即可,如下列数组

Keys

T	S	R	P	N	O	A
0	1	2	3	4	5	6

pq(用pq数组存储keys数组的索引，第二行是pq数组本身的索引)

0	1	2	3	4	5	6
1	2	3	4	5	6	7

        实现堆有序之后，两数组变为如下:

keys

T	S	R	P	N	O	A
0	1	2	3	4	5	6

pq（pq数组的0位置用不到，因为堆是从1位置开始的）

6

3

4

0

2

1

5

 

 如上两个数组，下方的整数型数组一一对应上方原始数组的索引，在实现堆有序过程中，不对原始数组改动，而只改动下方整数型数组的顺序，这样的话就能保证原始数组的顺序不变，从而保留其索引。

        但是还有个问题，索引优先队列API里有个delete(int k)的方法，在删除原始数组（keys）中的索引为k的元素时，同时也要删除pq数组的对应的值。但是并不知道其在pq中的索引，因此还需要一个整数型数组qp，来存储pq数组的逆序。

pq

	0	6	3	4	0	2	1	5
索引	0	1	2	3	4	5	6	7

qp

	4	6	5	2	3	7	1	-1
索引	0	1	2	3	4	5	6	7

       所以索引优先队列

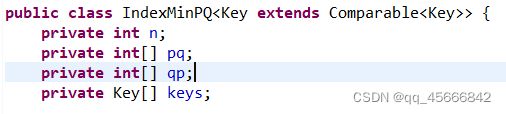
构造函数IndexMinPQ

public IndexMinPQ(int maxN)
{
    pq = new int[maxN+1];
    qp = new int[maxN+1];
    keys = (Key[]) new Comparable[maxN];
    for(int i = 0;i

insert(int k,Item item)方法

public void insert(int k,Key key)
{
    n++;
    pq[n] = k;
    qp[k] = n;
    keys[k] = key;
    swim(k);
}

   contains()方法

public boolean contains(int k)
{
    return qp[k] != -1;
}

isEmpty()方法

public booelan isEmpty()
{return n==0;}

min()方法

public Key min()
{
    return keys[pq[1]];
}

delMin()方法

public int delMIn()
{
    int indexOfmin = pq[1];
    exch(1,n--);
    sink(1);
    keys[pq[n+1]] = null;
    qp[pq[n+1]] = -1;
    return indexOfmin;
}

delete(int k)方法

public void delete(int k)
{   
    int index = qp[K];
    exch(index,n--);
    swim(index);
    sink(index);
    keys[k] = null;
    qp[pq[n+1]] = -1;
}

change(int k, Key key)

public void change(int k,Key key)
{
    keys[k] = key;
    int index = qp[k];
    swim(index);
    sink(index);
}

以上都是共有方法，要实现上述方法需要一些私有方法，如swim()、sink()、exch()、less()

private void swim(int k)
{
    while(k>1&&less(k,k/2))
    {
        exch(k,k/2);
        k = k/2;
    }
}

private void sink(int k)
{
    while(k<=n/2)
    {
        int j = 2*k;
        if(less(j