二分图的最大权匹配
二分图的最大权匹配
二分图的最大匹配
匈牙利算法
思路:将点分为两类,左边的点和右边的点。每次尝试给左边的点找一个右边的点与之匹配,
for (int i = 1; i <= n; ++i) {
Arrays.fill(st, false);//为什么要每次都要重置st
if (find(i)) res++;
}
for循环遍历左边的点,find(i)表示尝试给左边的i号节点找一个匹配点。
static boolean find(int u) {
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!st[j]) {//在本次匹配中j没有被访问过
st[j] = true;
if (match[j] == 0 || find(match[j])) {
match[j] = u;
return true;
}
}
}
return false;
}
for循环遍历与节点u相连的右边的点,如果右边的点还处在待匹配状态match[j] == 0,则让他与节点u匹配。如果右边的点已经被匹配,与之匹配的左边的点是match[j],尝试让match[j]匹配其它的右边点,所以有find(match[j])。那么这里要问,通过什么保证,我再次进入find函数的时候,不会与j匹配呢?那就是st函数,我们可以看见,在进行匹配时我优先判断了当前节点的st值是否为真,如果为真,表示当前这个节点已经被占用了,我就不能和他匹配了。那么我们最初进行find(u)的时候,只要进入了某个右边节点,我就把它的st值标为真,相当于先把他占有。如果find(match[j])返回为真,就说明当前的节点u可以和节点j匹配,否则就不行。这里注意st数组只对当前匹配有效,如果我要进行下一个左节点的匹配了,要先给他初始化一下。
二分图的最大权完美匹配
KM算法
主要思想:
要求最大权匹配,贪心的思路我想选权值最大的边进行匹配,除非这些边没有办法让我完成匹配,我再去选权值次大的边。
顶标和相等子图的概念:
左边的点标记一个左顶标,右边的点标记一个右顶标,如果一条边上连接的左右两个点的顶标之和等于边的权值,那么这条边就在相等子图里,在匹配的时候我们就可以用这条边。
初始化:
for(int i=1;i<=n;i++) la[i]=-INF;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
la[i]=Math.max(la[i],w[i][j]);//给左顶标初始化为最大值
for(int i=1;i<=n;i++) lb[i]=0;//给右顶标初始化为0
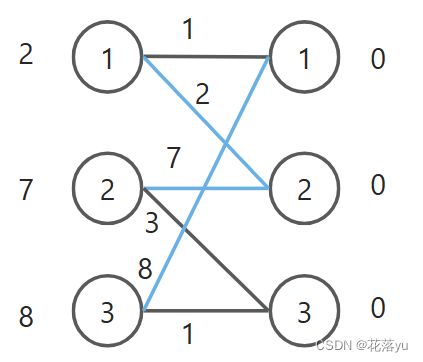
左顶标初始化为所连边的最大权值,右顶标初始化为0,此时相当于把左边点所连权值最大的边加入到了相等子图里,如下图所示,蓝色的边为当前可以用的边。
匈牙利算法进行匹配:
数组va用来标记左边的点是否在交替路中,数组vb用来标记右边的点是否在交替路中同时也表示右边的点在本次匹配过程是否被访问过。如果当前边在相等子图里,那么就尝试匹配。如果不在相等子图里,则记录当前边所连点的左右顶标之和与边权的差值,la[x]+lb[y]-w[x][y]。在匹配的过程中,我只使用蓝色的边。左边的1号点和右边的2号点匹配,左边的2号点也想和右边的2号点匹配,尝试让左边的1号点找其他匹配边,但是没有其他可用边了,匹配失败。
static boolean dfs(int x){//匈牙利算法
va[x]=1; //x在交替路中
for(int y=1;y<=n;y++){
if(vb[y]==0){//点是否可用
if(la[x]+lb[y]-w[x][y]==0){//相等子图 边是否可用
vb[y]=1; //y在交替路中
if(match[y]==0||dfs(match[y])){
match[y]=x; //配对
return true;
}
}
else //不是相等子图则记录最小的d[y]
d[x]=Math.min(d[x],la[x]+lb[y]-w[x][y]);
}
}
return false;
}
加入新的边:
接下来我们重点分析式子la[x]+lb[y]-w[x][y]
-
如果边(x,y)不在相等子图里,la[x]+lb[y]表示的是左边点x在相等子图里的边的最小值。 -
la[x]+lb[y]-w[x][y]相等子图里的边的最小值与不在相等子图里的边之差,注意一点,一旦要加边,必然是左边某两个点在匹配过程中发生了矛盾,还是刚刚那个例子,发生了失配,假设我要加一条与左节点1相连的边,其实就意味着让左节点1连当前加入的这条边,让他放弃原本的边,那么这个过程其实有一个代价,代价就是原本1号左节点能够连到的权值最小的边的权值减去当前加入边的权值。将(1,1)这条边加入的代价是2+0-1=1,这里的2+0就是1号点能够连到的权值最小的边的权值。将(2,3)这条边加入的代价是7+0-3=4,这里的7+0就是2号点能够连到的权值最小的边的权值。可以看见将边(1,1)加入付出的代价最小,所以将这条边加入。
为了将边(1,1)加入如何修改顶标?1号左节点顶标减1后,就将边(1,1)加入了,但是会产生“蝴蝶效应”,(1,2)边仍然要在相等子图里,1号左节点顶标减1,为了保持左右顶标之和不变,2号右节点顶标加1,(2,2)边仍然要在相等子图里,2号右节点顶标加1,为了保持左右顶标之和不变,2号左节点顶标减1。1其实就是最小的delta,重新构图的过程其实就是求最小的delta,然后左顶标加delta,右顶标减delta。哪些节点的顶标要发生变化呢?当然是在匹配过程中走到的节点,在代码里用va和vb标注了。
for(int i=1;i<=n;i++){//给每一个点寻找匹配点
while(true){//直到左点i找到匹配
Arrays.fill(va,0);
Arrays.fill(vb,0);
Arrays.fill(d,INF);
if(dfs(i))break;//走匈牙利算法
long delta=INF;
for(int j=1;j<=n;j++)
delta=Math.min(delta,d[j]);
for(int j=1;j<=n;j++){//修改顶标
if(va[j]!=0)la[j]-=delta;//左边的点-delta
if(vb[j]!=0)lb[j]+=delta;//右边的点+delta
}
}
}
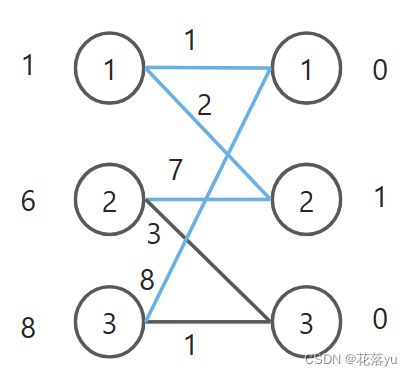
新建好的图如下,现在再走匈牙利算法,1号左节点和1号右节点匹配,2号左节点和2号右节点匹配,3号左节点也想和1号右节点匹配,再次发生失配。边(2,3)加入的代价是6+0-3=3,边(3,3)加入的代价是8+0-1=7,因此将边(2,3)加入。
新建好的图如下,现在再走匈牙利算法,1号左节点和1号右节点匹配,2号左节点和2号右节点匹配,3号左节点也想和1号右节点匹配,1号左节点和2号右节点匹配,2号左节点和3号右节点匹配,此时3号左节点可以和1号右节点匹配。